小白说编译原理-7-算术表达式编译树(支撑类)
前言
这个编译原理是一个系列,系列地址为: https://blog.csdn.net/lpstudy/article/category/937055
考虑到很多小伙伴咨询代码的问题,现把链接发出来:https://github.com/lpstudy/compile
这个链接里面具有这个系列所有的VS工程和代码,工程是按照系列中的一个教程环境配置6来配置的,不过lib我好像没有上传到github。
如果大家发现任何问题,可以在github或者csdn,我有空的时候完善一下,争取做到下载github工程即可跑。
简介
本章讲述的是编译树的实现,它包含树节点,树的构建,树的遍历三个部分。利用编译树,我们可以构建基本的运算节点以及数字节点,然后遍历树的过程就是执行算术运算的过程。
例如如下的一棵树
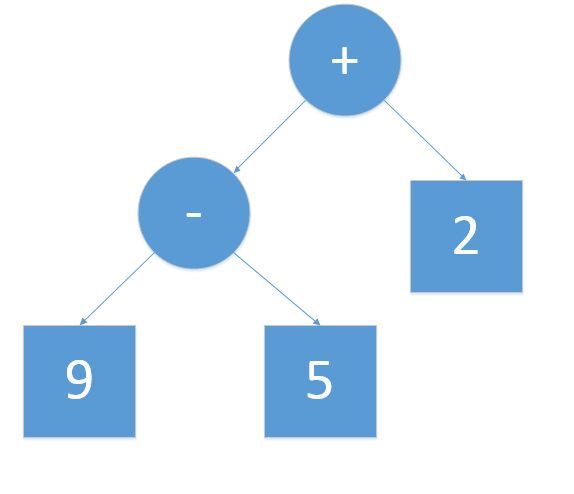
叶子节点和分支节点都是一个个的Node,它具有不同的类型(运算符和数字)。
代码如下
#include
#include
using namespace std;
#define MAX_CHILDREN 4
int my_mem[100]; // “内存”
int offset;
enum // 结点类型——kind
{
STMT_NODE = 0,
EXPR_NODE,
DECL_NODE
};
enum // 语句结点子类型——kindkind
{
IF_STMT = 0,
WHILE_STMT,
INPUT_STMT,
PRINT_STMT,
COMP_STMT
};
enum // 表达式结点子类型——kindkind
{
TYPE_EXPR = 0,
OP_EXPR,
NOT_EXPR,
ARRAY_EXPR,
CONST_EXPR,
ID_EXPR
};
enum // 声明结点子类型——kindkind
{
VAR_DECL = 0,
ARRAY_DECL
};
enum // 运算——op
{
PLUS = 0,
MINUS
};
enum
{
Integer = 0,
};
union NodeAttr {
int op; // 表达式结点,子类型是运算类型时,用op保存具体运算
int vali; // 表达式结点,常量表达式时,用vali保存整型常量值
char valc; // 字符值
NodeAttr(void) { op = 0; } // 几种构造函数
NodeAttr(int i) { op = i; }
NodeAttr(char c) { valc = c; }
};
struct Node
{
struct Node *children[MAX_CHILDREN]; // 孩子结点
int kind; // 结点类型
int kind_kind; // 子类型
NodeAttr attr; // 结点属性
int addr; // 分配的内存空间(数组下标)
};
class tree // 语法树类
{
private:
Node *root; // 根结点
private:
void recursive_get_addr(Node *t); // 为临时变量(如表达式)分配存储空间
void recursive_execute(Node *t); // 遍历树,执行源程序
public:
void setRoot(Node* p){root = p;}
Node *NewRoot(int kind, int kind_kind, NodeAttr attr, int type,
Node *child1 = NULL, Node *child2 = NULL, Node *child3 = NULL, Node *child4 = NULL); // 创建一个结点,设置其属性,连接孩子结点
void get_addr(void); // 分配空间和执行代码的接口
void execute(void);
};
Node * tree::NewRoot(int kind, int kind_kind, NodeAttr attr, int type,
Node *child1, Node *child2, Node *child3 , Node *child4)
{
Node* node = new Node();
node->kind = kind;
node->kind_kind = kind_kind;
node->attr = attr;
node->children[0] = child1;
node->children[1] = child2;
node->children[2] = child3;
node->children[3] = child4;
return node;
}
void tree::get_addr(void)
{
cout << "allocate memory..." << endl;
offset = 0;
recursive_get_addr(root); // 接口函数直接调用实际分配空间的递归函数
}
void tree::recursive_get_addr(Node *t)
{
if (t) { // 空指针什么也不做
if (t->kind == EXPR_NODE) { // 为表达式结点分配存储空间
t->addr = offset++;
//cout << t->addr << endl;
}
for (int i = 0; i < MAX_CHILDREN; i++) // 递归处理所有子树——先序遍历
recursive_get_addr(t->children[i]);
}
}
void tree::execute(void)
{
cout << "execute..." << endl;
recursive_execute(root); // 接口函数调用递归函数
cout << my_mem[root->addr] << endl; // 从内存取出执行结果,输出
}
void tree::recursive_execute(Node *t)
{
if (t) {
for (int i = 0; i < MAX_CHILDREN; i++) // 后序遍历
recursive_execute(t->children[i]);
if (t->kind == EXPR_NODE) // 表达式结点
if (t->kind_kind == OP_EXPR) { // 运算类型表达式
if (t->attr.op == PLUS) // 加法表达式
// 从内存(my_mem)中取出两个孩子的值,进行加法,结果写回内存
my_mem[t->addr] = my_mem[t->children[0]->addr] + my_mem[t->children[1]->addr];
else if (t->attr.op == MINUS) // 减法的处理类似加法
my_mem[t->addr] = my_mem[t->children[0]->addr] - my_mem[t->children[1]->addr];
}
else if (t->kind_kind == CONST_EXPR) // 常量表达式,将值(在vali中)保存至分配的内存中
my_mem[t->addr] = t->attr.vali;
}
}
int main(int argc, char *argv[])
{
tree expr;
Node *p, *q, *r;
// 创建结点9
p = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(9), Integer);
// 创建结点5
q = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(5), Integer);
// 创建减法结点,孩子结点为9和5
r = expr.NewRoot(EXPR_NODE, OP_EXPR, NodeAttr(MINUS), Integer, p, q);
q = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(2), Integer);
p = expr.NewRoot(EXPR_NODE, OP_EXPR, NodeAttr(PLUS), Integer, r, q);
expr.setRoot(r);
expr.get_addr(); // 为(子)表达式(们)分配存储空间
expr.execute(); // 执行代码
}
代码解释
节点类型: 句子节点,表达式节点和变量定义节点。
节点类型的子类型,只说明句子,包含If语句,while语句,输入输出语句等等。
struct Node: 表示树中的一个节点,它有多个孩子节点,以及节点的类型,节点存储数据的地址和节点属性
class tree: 表示一颗语法树,包含树的遍历方法和分配内存的方法。
recursive_execute: 树的遍历方法
if (t->kind_kind == OP_EXPR) { // 运算类型表达式
if (t->attr.op == PLUS) // 加法表达式
// 从内存(my_mem)中取出两个孩子的值,进行加法,结果写回内存
my_mem[t->addr] = my_mem[t->children[0]->addr] + my_mem[t->children[1]->addr];
else if (t->attr.op == MINUS) // 减法的处理类似加法
my_mem[t->addr] = my_mem[t->children[0]->addr] - my_mem[t->children[1]->addr];
}
else if (t->kind_kind == CONST_EXPR) // 常量表达式,将值(在vali中)保存至分配的内存中
my_mem[t->addr] = t->attr.vali;
首先对数的所有孩子进行遍历执行,得到它的孩子的执行结果。
然后查看当前节点的类型,如果当前是表达式类型,且是加法,那么就将两个孩子的数据相加,每个孩子有一个addr属性保存它对应的地址值。如果节点是CONST数据类型,那么直接将节点对应地址的内容设置为对应的数据。
recursive_get_addr: 分配内存的方法
void tree::recursive_get_addr(Node *t)
{
if (t) { // 空指针什么也不做
if (t->kind == EXPR_NODE) { // 为表达式结点分配存储空间
t->addr = offset++;
//cout << t->addr << endl;
}
for (int i = 0; i < MAX_CHILDREN; i++) // 递归处理所有子树——先序遍历
recursive_get_addr(t->children[i]);
}
}
上述函数递归给表达式节点分配内存,这是因为语句节点并不具有值的概念,只有表达式节点才有值,才需要分配内存以存储执行结果。
main:构造表达式树,并执行
int main(int argc, char *argv[])
{
tree expr;
Node *p, *q, *r;
// 创建结点9
p = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(9), Integer);
// 创建结点5
q = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(5), Integer);
// 创建减法结点,孩子结点为9和5
r = expr.NewRoot(EXPR_NODE, OP_EXPR, NodeAttr(MINUS), Integer, p, q);
q = expr.NewRoot(EXPR_NODE, CONST_EXPR, NodeAttr(2), Integer);
p = expr.NewRoot(EXPR_NODE, OP_EXPR, NodeAttr(PLUS), Integer, r, q);
expr.setRoot(r);
expr.get_addr(); // 为(子)表达式(们)分配存储空间
expr.execute(); // 执行代码
}
上述代码创建5个节点,并通过传入的参数来确定节点的类型,值以及它们与孩子的对应关系,其代码表达的树就是上面图中的那颗树。最后设置根节点,然后分配内存,后序遍历执行。