花式骚操作之聚类--方法汇总详解附代码

fcm聚类

模糊聚类是目前知识发现以及模式识别等诸多领域中的重要研究分支之一。随着研究范
围的拓展，不管是科学研究还是实际应用，都对聚类的结果从多方面提出了更高的要求。模糊
C-均值聚类(FCM)是目前比较流行的一种聚类方法。该方法使用了在欧几里得空间确定数
据点的几何贴近度的概念，它将这些数据分配到不同的聚类,然后确定这些聚类之间的距离。
模糊C-均值聚类算法在理论和应用上都为其他的模糊聚类分析方法奠定了基础,应用也最
广泛。但是，从本质上FCM算法是一种局部搜索优化算法，如果初始值选择不当,它就会收
敛到局部极小点上。因此，FCM算法的这一缺点限制了人们对它的使用。

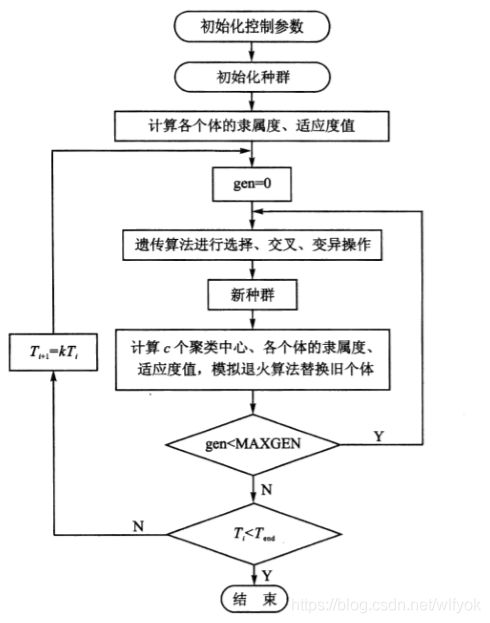
基于SAGA的聚类

我们将模拟退火算法与遗传算法相结合(SAGA)用于聚类分析，由于模拟退火算法和遗
传算法可以互相取长补短,因此有效地克服了传统遗传算法的早熟现象，同时根据聚类问题的
具体情况设计遗传编码方式及适应度函数，使该算法更有效.更快速地收敛到全局最优解。

快速聚类

基本思想是，样本容量较大时，选择一批凝聚点
或给出一个初始的分类，让样品按某种原则向凝聚点
凝聚，对凝聚点进行不断的修改或迭代，直至分类比
较合理或迭代稳定为止。
类的个数k可以事先指定，也可以在聚类过程中
确定。选择初始凝聚点(或给出初始分类)的一种简
单方法是采用随机抽选(或随机分割)样品的方法。
动态聚类法有许多种方法，本节中，只讨论一种
比较流行的动态聚类法——k均值法。k均值法是由麦
奎因(MacQueen,1967)提出并命名的一种算法。

系统聚类

系统聚类法（hierarchical cluster method）一译“分层聚类法”。聚类分析的一种方法。其做法是开始时把每个样品作为一类，然后把最靠近的样品（即距离最小的群品）首先聚为小类，再将已聚合的小类按其类间距离再合并，不断继续下去，最后把一切子类都聚合到一个大类。
它的步骤如下：
以n个样本的聚类分析为例，系统聚类法的步骤如下：
定义以变量或指标的个数为维度的空间里的一种距离；
计算n个样本两两之间的距离；
将每个样本归为一类，根据计算出的样本间的距离合并距离最近的两类为一个新类；
再计算新类与其他各类的距离，同样再根据计算出的距离合并距离最近的两类为一个新类；
循环以上过程直至类别个数为1；
画出各阶段的聚类图并决定类别的个数。
对于变量聚类分析，只需要将距离替换为相似系数，然后将相似系数较大的变量分别聚类即可。

两步聚类

两步聚类算法是一种聚类算法，是BIRCH层次聚类算法的改进版本。可以应用于混合属性数据集的聚类，同时加入了自动确定最佳簇数量的机制，使得方法更加实用。本文在学习文献[1]和“IBM SPSS Modeler 15 Algorithms Guide”的基础上，融入了自己的理解，更详尽地叙述两步聚类算法的流程和细节。
两步聚类算法，顾名思义分为两个阶段：

1）预聚类（pre-clustering）阶段。采用了BIRCH算法中CF树生长的思想，逐个读取数据集中数据点，
在生成CF树的同时，预先聚类密集区域的数据点，形成诸多的小的子簇（sub-cluster）。

2）聚类（clustering）阶段。以预聚类阶段的结果——子簇为对象，利用凝聚法
（agglomerative hierarchical clustering method），逐个地合并子簇，直到期望的簇数量。

题目

将400个随机生成的二维平面上的点进行合理的聚类分析，最终得出适合的k值及不同聚类下的点的集合。这里我们用MATLAB生成400个随机点，其命令如下

X = rand(400,2);

接下来，我们就利用上面所介绍的五种聚类方法对我们的数据集中的点进行合理的聚类，得到的结果如下面所示，也附有代码哦。

结果及代码

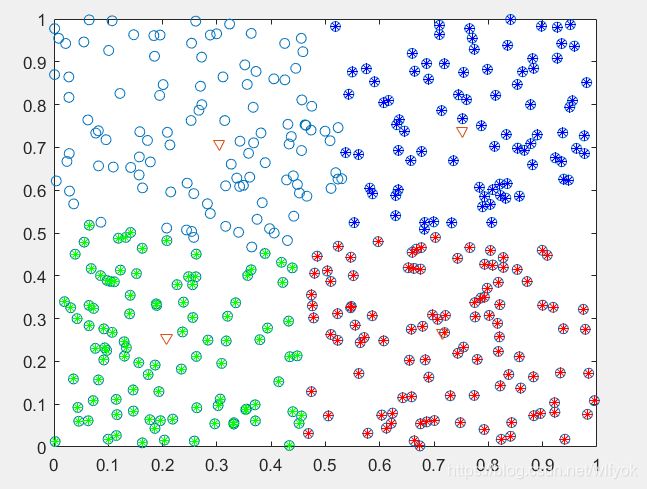
                                               快速聚类的结果

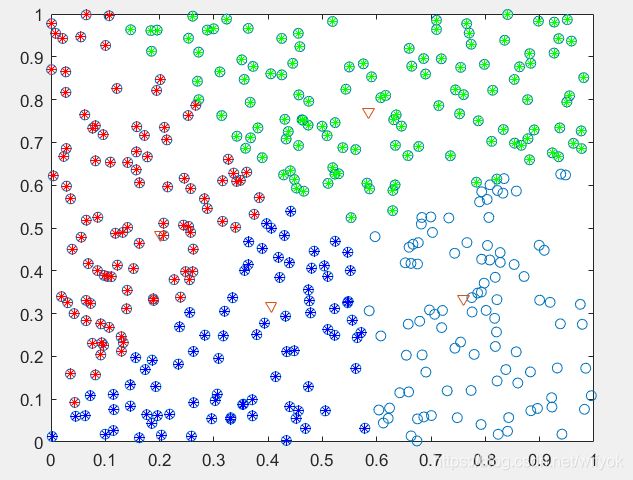
                                                系统聚类结果

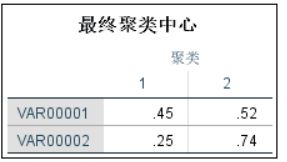
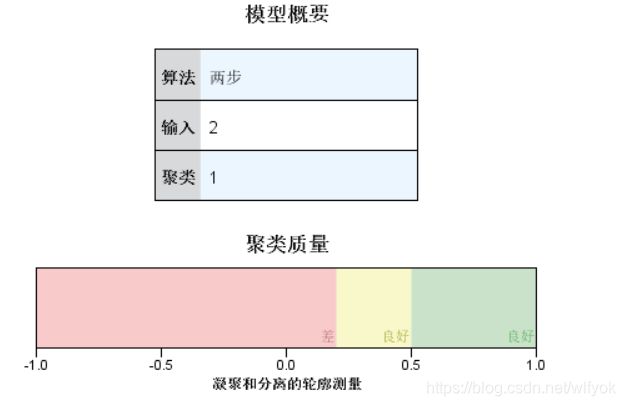
                                            两步聚类结果

                                      基于saga聚类结果图

                                             普通fcm聚类的结果

% saga主函数
% 其中部分使用Sheffield工具箱的函数
clear
clc
x = xlsread('X.xlsx');
m = size(x,2);
lb = min(x);
ub = max(x);
% 初始化
options = [3,20,1e-6];
cn = 4;
% sa算法的参数
q = 0.8;            % 冷却系数
t0 = 100;           % 初始温度
tend = 1;           % 终止温度
% ga参数
sizepop = 10;
maxgen = 10;
nvar = m*cn;
preci = 10;
ggap = 0.9;
pc = 0.7;
pm = 0.01;
trace = zeros(nvar+1,maxgen);
field = [rep([preci],[1,nvar]);rep([lb;ub],[1,cn]);rep([1;0;1;1],[1,nvar])];
chrom = crtbp(sizepop,nvar*preci);
v = bs2rv(chrom,field);
objv = ObjFun(x,cn,v,options);
t = t0;
while t > tend
    gen = 0;
    while gen < maxgen
        fitnv = ranking(objv);
        selch = select('sus',chrom,fitnv,ggap);
        selch = recombin('xovsp',selch,pc);
        selch = mut(selch,pm);
        v = bs2rv(selch,field);
        objvsel = ObjFun(x,cn,v,options);
        [newchrom newobjv] = reins(chrom,selch,1,1,objv,objvsel);
        v = bs2rv(newchrom,field);
        % 是否替换旧个体
        for i = 1:sizepop
            if objv(i) > newobjv(i)
                objv(i) = newobjv(i);
                chrom(i,:) = newchrom(i,:);
            else
                p = rand;
                if p <= exp((newobjv(i) - objv(i))/t);
                    objv(i) = newobjv(i);
                    chrom(i,:) = newchrom(i,:);
                end
            end
        end
        gen = gen + 1;
        [trace(end,gen),index] = min(objv);
        trace(1:nvar,gen) = v(index,:);
        fprintf(1,' %d',gen);
    end
    t = t*q;
    fprintf(1,'\n温度：%1.3f\n',t);
end
[newobjv,center,u] = ObjFun(x,cn,[trace(1:nvar,end)]',options);
% 查看聚类结果
jb = newobjv;
u = u{
     1};
center = center{
     1};
figure
plot(x(:,1),x(:,2),'o')
hold on 
maxu = max(u);
index1 = find(u(1,:) == maxu);
index2 = find(u(2,:) == maxu);
index3 = find(u(3,:) == maxu);
% 在前三类样本数据中分别画上不同记号，不加记号的就是第四类
line(x(index1,1),x(index1,2),'linestyle','none','marker','*','color','g');
line(x(index2,1),x(index2,2),'linestyle','none','marker','*','color','r');
line(x(index3,1),x(index3,2),'linestyle','none','marker','*','color','b');
% 画出聚类中心
plot(center(:,1),center(:,2),'v')
hold off

function [unew,center,objfcn] = iteratefcm(x,u,cluster_n,b)
% 开始迭代计算
mf = u.^b;
center = mf*x./((ones(size(x,2),1)*sum(mf'))');   % 更新后的聚类中心
dist = distfcm(center,x);
objfcn = sum(sum((dist.^2).*mf));               % 目标函数值
% 计算新的u
temp = dist.^(-2/(b-1));
unew = temp./(ones(cluster_n,1)*sum(temp));

function u = initfcm(x,cluster_n,center,b)
% 初始化相似分类矩阵
dist = distfcm(center,x);
% 开始计算新的u
temp = dist.^(-2/(b-1));
u = temp./(ones(cluster_n,1)*sum(temp));

function [obj,center,u] = fcmfun(x,cluster_n,center,options)
% fcm主函数
% X 样本数据
% cluster_n 聚类数
xn = size(x,1);
inn = size(X,2);
b = options(1);
maxiter = options(2);
minimpro = options(3);
objfcn = zeros(maxiter,1);
u = initfcm(x,cluster_n,center,b);
% 开始循环
for i = 1:maxiter
    [u,center,objfcn(i)] = iteratefcm(x,u,cluster_n,b);
    % 校验终止条件
    if i > 1
        if abs(objfcn(i) - objfcn(i-1)) < minimpro
            break;
        end
    end
end
itern = i;
objfcn(itern+1:maxiter) = [];
obj = objfcn(end);

% 使用fcm聚类
clear
clc
X = xlsread('X.xlsx');
figure
plot(X(:,1),X(:,2),'O')
hold on
% 参数设置
options = [3 20 1e-6 0];
% 聚类数
cn = 4;
[center,U,obj_fcn] = fcm(X,cn,options);
jb = obj_fcn(end);
maxU = max(U);
index1 = find(U(1,:) == maxU);
index2 = find(U(2,:) == maxU);
index3 = find(U(3,:) == maxU);
% 对前三类样本数据标号，没标号的就是第四类
line(X(index1,1),X(index1,2),'linestyle','none','marker','*','color','g');
line(X(index2,1),X(index2,2),'linestyle','none','marker','*','color','r');
line(X(index3,1),X(index3,2),'linestyle','none','marker','*','color','b');
% 画出聚类中心
plot(center(:,1),center(:,2),'v')
hold off