R语言实现 黑箱方法——神经网络

用人工神经网络对混泥土的强度strength进行建模** ----

Step 1: Exploring and preparing the data ----探索与准备数据

以下有8个描述混合物成分的特征

read in data and examine structure读入数据

concrete <- read.csv("F:\\rwork\\Machine Learning with R (2nd Ed.)\\Chapter 07\\concrete.csv")
str(concrete)

custom normalization function
自己写一个函数将数据转化为0-1之间

normalize <- function(x) { 
  return((x - min(x)) / (max(x) - min(x)))}

apply normalization to entire data frame
应用上面的函数对数据进行处理

concrete_norm <- as.data.frame(lapply(concrete, normalize))

检查一下是否转化完成
confirm that the range is now between zero and one

summary(concrete_norm$strength)

compared to the original minimum and maximum

summary(concrete$strength)

create training and test data一部分做为训练数据，一部分作为测试数据

concrete_train <- concrete_norm[1:773, ]
concrete_test <- concrete_norm[774:1030, ]

Step 2: Training a model on the data ----训练模型

train the neuralnet model

#install.packages('neuralnet')#如果没有安装记得安装一下哦~
library(neuralnet)

simple ANN with only a single hidden neuron
单一隐藏节点的最简单的多层前馈网络

set.seed(12345) # to guarantee repeatable results
concrete_model <- neuralnet(formula = strength ~ cement + slag +
                              ash + water + superplastic + 
                              coarseagg + fineagg + age,
                              data = concrete_train)

visualize the network topology
网络拓扑结构可视化

plot(concrete_model)

对于8个特征中的每一个特征都有输入节点，后面跟着一个单一的隐藏节点和一个单一的预测混凝土的输出节点。
偏差项（bias term）也被描绘出来（通过带有数字1的节点表述）。
图的底部，R报告了训练的步数和误差平方和（SSE），较低的SSE意味着更好的预测性能

Step 3: Evaluating model performance ----评估模型性能

网络拓扑结构图让我们窥视了人工神经网络的黑箱，但是并没有提供更多关于模型拟合未来数据好坏的消息。
为了生成关于测试数据集的预测值，进行如下操作：
obtain model results

model_results <- compute(concrete_model, concrete_test[1:8])

compute和predict的运算原理不一样,它会返回一个带有两个分量的列表：
$neurons，用来储存网络中每一层的神经元；
$net.result，用来储存预测值

obtain predicted strength values

predicted_strength <- model_results$net.result#获得预测值

examine the correlation between predicted and actual values
计算预测值与真实值之间的相关性

cor(predicted_strength, concrete_test$strength)

相关性接近1表示两个变量之间具有很强的线性关系。因此，这里面大约为0.806的相关性表示具有一个相当强的线性关系。这意味着计数只有一个单一的隐藏点，我们的模型也做了相当不错的工作。
考虑到只用了一个隐藏点，因此我们模型的性能很可能可以提高。我们试着建立一个更好的模型。

Step 4: Improving model performance ----提高模型性能

a more complex neural network topology with 5 hidden neurons
这里我们将隐藏节点增加到5

set.seed(12345) # to guarantee repeatable results
concrete_model2 <- neuralnet(strength ~ cement + slag +
                               ash + water + superplastic + 
                               coarseagg + fineagg + age,
                               data = concrete_train, hidden = 5)

plot the network

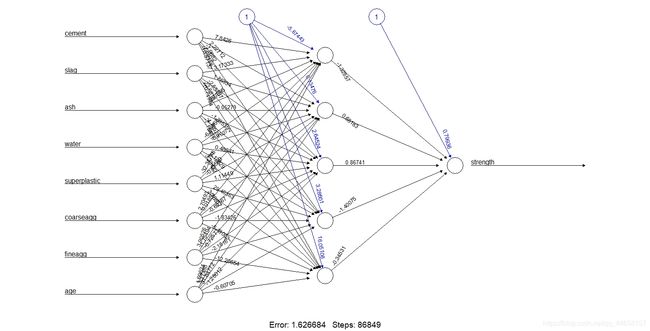
plot(concrete_model2)

从图中我们可以发现SSE已经从原先的5.08降到了1.63。此外，训练步数也从4882增加到了86849，考虑到现在的模型已经变得多复杂，这也就不足为奇了。越复杂的神经网络需要越多的跌倒来找到最优的权重。

evaluate the results as we did before

model_results2 <- compute(concrete_model2, concrete_test[1:8])
predicted_strength2 <- model_results2$net.result
cor(predicted_strength2, concrete_test$strength)

采用相同的步骤对预测值和真实值进行比较，现在我们获取的相关系数大约为0.92，与之前具有的单个隐藏点的结果0.80相比，这是一个相当大的改进。

欢迎指正哦~~~（需要数据私聊邮箱哦~）