FCM算法的matlab实现(Fuzzy C-means 算法)
FCM算法
- $FCM$算法简介
- $FCM$算法原理
- $FCM$算法实现$(matlab)$
F C M FCM FCM算法简介
F C M FCM FCM算法属于划分式聚类算法,用模糊的方法来处理聚类问题,他从一个初始划分开始,需要预先指定聚类数目,还需要定义一个最优化聚类标准,也就是目标函数,作为度量各类样本分布的代价函数。 F C M FCM FCM把N个数据向量分为 C C C个模糊类,用每个类的聚类中心代表该类。通过反复的迭代运算,逐步降低目标函数的误差值,当目标函数收敛时,可得到最终的聚类结果。
F C M FCM FCM算法原理
符号说明:
x i x_i\quad xi 第 i i i个样本
N N\quad N 样本的个数
l l\quad l 样本的维度
C C\quad C 划分的样本的类别
V V\quad V 聚类中心
u i k u_{ik}\quad uik第 i i i个数据点属于第k类的隶属度
d ( x i , v k ) d(x_i,v_k)\quad d(xi,vk) 第 i i i个样本到第 k k k聚类中心的欧氏距离,即 d ( x i , v k ) = ∑ p = 1 L ( x i p − v k p ) 2 d(x_i,v_k)=\sqrt{\sum_{p=1}^L(x_{ip}-v_{kp})^2} d(xi,vk)=∑p=1L(xip−vkp)2
F C M FCM FCM算法的目标函数定义为:
J F C M ( u , v ) = ∑ k = 1 C ∑ i = 1 N u i k m d 2 ( x i , v k ) J_{FCM}(u,v)=\sum_{k=1}^C\sum_{i=1}^Nu_{ik}^md^2(x_i,v_k) JFCM(u,v)=k=1∑Ci=1∑Nuikmd2(xi,vk)
其中隶属度的约束条件为:
∑ k = 1 C u i k = 1 i = 1 , 2 , . . . , N \sum_{k=1}^Cu_{ik}=1 \quad i=1,2,...,N k=1∑Cuik=1i=1,2,...,N
将欧式距离带入到目标函数公式:
J F C M ( u , v ) = ∑ i = 1 N ∑ k = 1 C ( u i k 2 ) ∑ p = 1 L ( x i p − v k p ) 2 k ∈ { 1 , 2 , . . . C } p ∈ { 1 , 2 , . . . L } J_{FCM}(u,v)=\sum_{i=1}^N\sum_{k=1}^C(u_{ik}^2)\sum_{p=1}^L(x_{ip}-v_{kp})^2\quad k\in{\{1,2,...C}\}\quad p\in{\{1,2,...L\}} JFCM(u,v)=i=1∑Nk=1∑C(uik2)p=1∑L(xip−vkp)2k∈{ 1,2,...C}p∈{ 1,2,...L}
对 v k p v_{kp} vkp求偏导数,并令其为零,得:
∂ J F C M ∂ v k p = 2 ∑ i = 1 N ( u i k ) 2 ( x i p − v k p ) \frac{\partial{J_{FCM}}}{\partial v_{kp}} =2\sum_{i=1}^N (u_{ik})^2(x_{ip}-v_{kp}) ∂vkp∂JFCM=2i=1∑N(uik)2(xip−vkp)
2 ∑ i = 1 N ( u i k ) 2 ( x i p − v k p ) = 0 2\sum_{i=1}^N(u_{ik})^2(x_{ip}-v_{kp})=0 2i=1∑N(uik)2(xip−vkp)=0
解得:
v k p = ∑ i = 1 2 ( u i k ) 2 x i p ∑ i = 1 N ( u i k ) 2 v_{kp}=\frac{\sum_{i=1}^2(u_{ik})^2x_{ip}}{\sum_{i=1}^N(u_{ik})^2} vkp=∑i=1N(uik)2∑i=12(uik)2xip
构造拉格朗日函数:
J F C M ( u , v , λ ) = ∑ i = 1 N ∑ k = 1 C ( u i k ) 2 d 2 ( x i − v k ) − ∑ i = 1 N λ i ( ∑ k = 1 C u i k − 1 ) J_{FCM}(u,v,\lambda)=\sum_{i=1}^N\sum_{k=1}^C(u_{ik})^2{d^2(x_{i}-v_{k})}-\sum_{i=1}^N\lambda_i(\sum_{k=1}^Cu_{ik}-1)\quad JFCM(u,v,λ)=i=1∑Nk=1∑C(uik)2d2(xi−vk)−i=1∑Nλi(k=1∑Cuik−1)
r ∈ { 1 , 2 , . . . N } s ∈ { 1 , 2 , . . . C } r\in{\{ 1,2,...N\}} s\in{\{ 1,2,...C\}} r∈{ 1,2,...N}s∈{ 1,2,...C}
对 u r s u_{rs} urs求偏导数并令其为零,得:
∂ J F C M ( u , v ) ∂ u r s = 2 ( u u s d 2 ( x r − λ r ) ) = 0 \frac{\partial {J_{FCM}(u,v)}}{\partial u_{rs}}=2(u_{us}d^2(x_r-\lambda_r))=0 ∂urs∂JFCM(u,v)=2(uusd2(xr−λr))=0
u r s = λ r 2 d 2 ( x r , v s ) u_{rs}=\frac{\lambda_r}{2d^2{(x_r,v_s)}} urs=2d2(xr,vs)λr
考虑到约束条件, ∑ k = 1 C u r k = 1 \sum_{k=1}^Cu_{rk}=1 ∑k=1Curk=1,得: ∑ k = 1 C λ r 2 d 2 ( x r , v k ) = 1 \sum_{k=1}^C\frac{\lambda_r}{2d^2(x_r,v_k)}=1 ∑k=1C2d2(xr,vk)λr=1,即:
λ r = 1 ∑ k = 1 C 1 2 d 2 ( x r , v k ) \lambda_r=\frac{1}{\sum_{k=1}^C\frac{1}{2d^2(x_r,v_k)}} λr=∑k=1C2d2(xr,vk)11
将 λ r \lambda_r λr带入可得:
v k = ∑ i = 1 N ( u i k ) m x i ∑ i = 1 N ( u i k ) m v_k=\frac{\sum_{i=1}^N(u_{ik})^m x_i}{\sum_{i=1}^N(u_{ik})^m} vk=∑i=1N(uik)m∑i=1N(uik)mxi
隶属度的更新公式为:
u i k = 1 d 2 ( x i , v k ) ∑ r = 1 C 1 d 2 ( x i , v r ) u_{ik}=\frac{ \frac{1} {d^2(x_i,v_k)} }{ {\sum_{r=1}^C }\frac{1} {d^2(x_i,v_r)}} uik=∑r=1Cd2(xi,vr)1d2(xi,vk)1
F C M FCM FCM算法实现 ( m a t l a b ) (matlab) (matlab)
一共有的四个函数:
主函数 FCMCluster.m
模糊矩阵初始化:initfcm.m
欧氏距离distfcm.m
逐次聚类:stepfcm.m
function [center,U,obj_fun]=FCMCluster(data,n,options)
% 采用模糊c均值聚类,将数据集分为n类
% data 数据集 n 类别数
% options 4*1 矩阵
% option(1):隶属度函数矩阵的加权指数,默认为2
% option(2):最大迭代次数,默认100次
% option(3):隶属度最小变化量,默认为1e-5
% option(4):每次迭代是否输出信息标志,默认输出,值为1
% center 聚类中心
% U 隶属度矩阵
% obj_fun 目标函数值
%确定或给定参数
if nargin~=2 && nargin ~=3
error('Too many ot too few input agruments');
end
%默认参数
default_options=[2;100;1e-5;1];
% 参数配置
if nargin==2
options=default_options;
else
if length(options)<4
tmp=default_options;
tmp(1:length(options))=options;
options=tmp;
end
nan_index=find(isnan(options)==1);
options(nan_index)=default_options(nan_index);
if options(1)<=1
error('The exponent should be greater than 1!');
end
end
%参量初始化
expo=options(1); %指数的次幂
max_iter=options(2); %最大迭代次数
min_impro=options(3); %精度
display=options(4); %是否显示最终函数值
obj_fun=zeros(max_iter,1); %储存聚类函数在每次迭代中的值
data_n=size(data,1); %行数,即样本个数
in_n=size(data,2); %样本的维数
U=initfcm(n,data_n); % 初始化模糊分配矩阵
% 主程序
for i=1:max_iter
[U,center,obj_fun(i)]=stepfcm(data,U,n,expo);
%显示聚类最终的函数值
if display
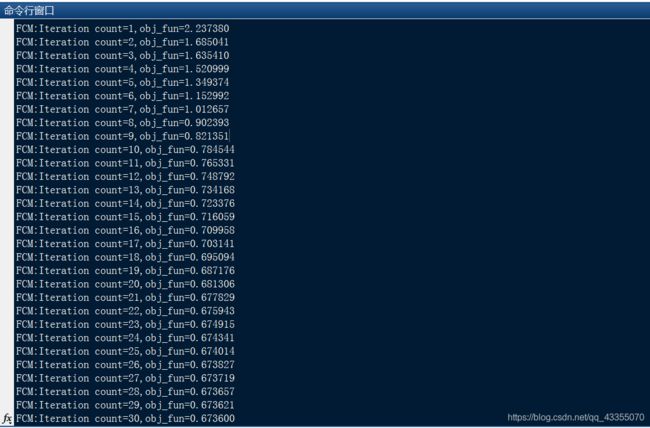
fprintf('FCM:Iteration count=%d,obj_fun=%f\n',i,obj_fun(i));
end
% 终止条件判断
if i>1
if abs(obj_fun(i)-obj_fun(i-1))function U=initfcm(n,data_n)
%子函数 模糊矩阵初始化
% data_n 样本个数
% n 分类个数
% U(i,j) 第j个数据点属于第i个类的隶属度
%取随机矩阵,且进行归一化(即,列和为1)
U=rand(n,data_n);
col_sum=sum(U);
U=U./col_sum(ones(n,1),:);
end
function [U_new,center,obj_fun]=stepfcm(data,U,n,expo)
% 逐步聚类
%聚类中心
mf=(U.^expo);
center=mf*data./((ones(size(data,2),1)* sum(mf'))');
%聚类函数对应函数值
dist=distfcm(center,data);
obj_fun=sum( sum( (dist.^2).* mf) );
%更新隶属度矩阵
tmp=dist.^(-2/(expo-1));
U_new=tmp./(ones(n,1)*sum(tmp));
end
function out=distfcm(center,data)
% 计算样本到聚类中的距离,欧几里得距离
out = zeros(size(center,1),size(data,1));
for k=1:size(center,1)
out(k,:)=sqrt( sum(((data-ones(size(data,1),1) * center(k,:)).^2)',1));
end
end
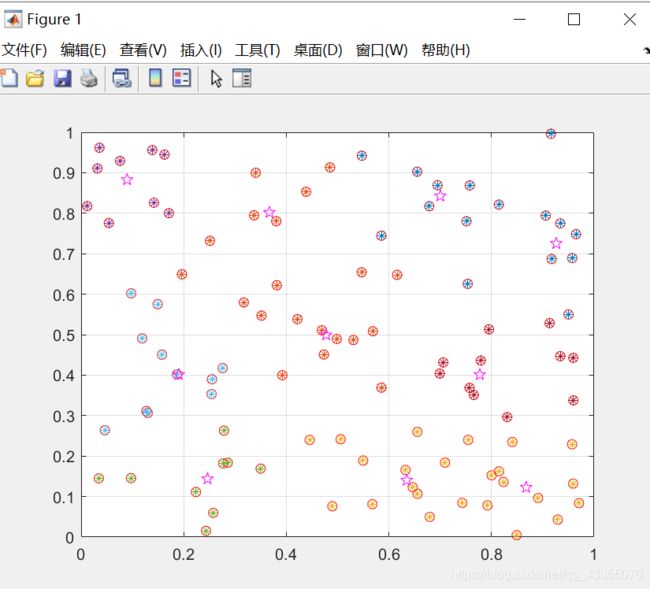
下面利用随机生成的100个二维数据来对算法进行验证:
function fmean
clear,clc
close all
data=rand(100,2);
N=10;
[center,U,obj_fcn]=FCMCluster(data,N);
plot(data(:,1),data(:,2),'ro');
hold on
U_max=max(U);
for j=1:100
row(:,j)=find(U(:,j)==U_max(j)); %列数对应相应的数据位置,矩阵元素对应其类别
end
for i=1:N
col=find(row==i); %max(U)返回隶属度列最大值所在行一致的分为一类
plot(data(col,1),data(col,2),'*');
hold on
end
grid on
%画出聚类中心
plot(center(:,1),center(:,2),'p','color','m','MarkerSize',8);
end