线性回归知识总览
博文内容为
- 机器学习的一些概念
有监督、无监督、泛化能力、过拟合欠拟合(方差和偏差以及各自解决办法)、交叉验证 - 线性回归的原理
- 线性回归损失函数、代价函数、目标函数
- 优化方法(梯度下降法、牛顿法、拟牛顿法等)
- 线性回归的评估指标
- sklearn参数详解
机器学习的一些概念
机器学习分类:
-
按数据分类
-
分类、回归、序列标注
-
按模型分类
-
生成式模型、判别式模型
-
按监督分类
-
有监督、无监督
统计学习包括监督学习、非监督学习、半监督学习及强化学习。
监督学习(supervised learning):
输入数据是有标签的,通过学习一个模型,使得模型能够对任意给定输入(可理解为自变量 X ),对其相应的输出给出一个预测 y ^ \hat{y} y^,经典算法包括支持向量机、逻辑回归、决策树,以及概率图模型:朴素贝叶斯、最大熵模型、隐马尔科夫模型、条件随机场等。
无监督学习:
给机器输入无标签的数据,希望通过模型挖掘数据中存在的某种共性特征、关联或者结构。非监督学习主要包括两大类学习方法:数据聚类和特征变量关联。其中,数据聚类使用过多次迭代跟新,找到数据的最优分割,而特征变量关联则是 利用各种相关性方法来找到变量之间的关系。
层次聚类、K均值聚类、主题模型等。
泛化能力,过拟合,欠拟合:
泛化能力一般是对于有监督模型,第一阶段,训练模型,会将已有的带标签数据集进行划分,分为训练集和测试集;第二阶段,应用模型,在新的数据集(预测集)上应用模型,获得数据标签的预测。模型的泛化能力,指的是在第二阶段预测数据集上评估指标的表现。见下表:
| 效果/数据集 | 训练集 | 预测集 | 结果 |
|---|---|---|---|
| 效果 | 好 | 好 | 泛化能力强 |
| 好 | 差 | 过拟合、泛化能力弱 | |
| 差 | 差 | 欠拟合 |
降低“过拟合”风险:
1.数据方面:增加数据
2.降低模型复杂度:在数据较少是,模型过于复杂是产生过拟合的主要因素。减少线性模型高次项,神经网络中减少网络层数、神经元个数等;在决策树模型中降低树的深度、进行剪纸等。
3.正则化
4.集成学习:降低单一模型的过拟合风险,防止一家独大
5.dropout
降低“欠拟合”风险:
1.增加特征:当特征不足或者特征与样本标签的相关性不强时,模型容易出现欠拟合。
2.增加模型复杂度
3.减小正则化系数
- 牛顿法参考内容
交叉验证(Cross Validation)
交叉验证(Cross Validation),有的时候也称作循环估计(Rotation Estimation),是一种统计学上将数据样本切割成较小子集的实用方法。K折交叉验证(K-fold cross-validation),留一法(LOOCV)交叉验证。
和我们常见的训练集和测试集划分不同的是,交叉验证涉及数据的交叉使用:
在给定的建模样本中,拿出大部分样本进行建模型,留小部分样本用刚建立的模型进行预报,并求这小部分样本的预报误差,记录它们的平方加和。这个过程一直进行,直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和,称为PRESS(predicted Error Sum of Squares)。
损失函数、代价函数、目标函数
监督学习中对数据进行建模得到模型 f f f,模型对给与的输入样本 X X X,由 f ( X ) f(X) f(X)给出相应的输出 Y ^ \hat{Y} Y^,这个输出值与真实值 Y Y Y可能一致也可能不一致,如何衡量错误的程度呢?,引入一个非负实函数,计作 L ( Y , f ( X ) ) L(Y,f(X)) L(Y,f(X)),为损失函数(loss function)
基本概念:
损失函数:计算的是一个样本的误差
代价函数:是整个训练集上所有样本误差的平均
目标函数:代价函数 + 正则化项
(经验风险最小化+结构风险最小化)
实际应用中:损失函数和代价函数都是来度量预测值与真实值之间的差异,区分不大。
损失函数越小,就代表模型拟合的越好。那是不是我们的目标就只是让loss function越小越好呢?还不是。这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望,这是由于我们输入输出的(X,Y)遵循一个联合分布,但是这个联合分布是未知的,所以无法计算。但是我们是有历史数据的,就是我们的训练集,f(X)关于训练集的平均损失称作经验风险(empirical risk),所以我们的目标就是最小化经验风险。
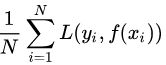
同时,对于模型来说,越复杂的模型拟合数据越好,但是会带来过拟合风险,这就引出了结构风险概念,我们不仅要让经验风险最小化,还要让结构风险最小化。
这个时候就定义了一个函数J(f),这个函数专门用来度量模型的复杂度,在机器学习中也叫正则化(regularization)。常用的有L1, L2范数。到这一步我们就可以说我们最终的优化函数是:

监督学习问题就变成经验风险或者结构风险函数的最优化问题,这时经验或者结构风险函数是最优化的目标函数。
线性回归的原理
通俗来说是对于样本点,将其描绘在坐标轴上,通过找到一条直线去刻画数据的分布,尽力找到一条直线使得尽可能多的样本点落在直线上或分布在直线周围。

线性回归
1 理解回归
回归分析的目的是利用变量间的简单函数关系,用自变量对因变量进行“预测”,使“预测值”尽可能地接近因变量的“观测值”。
2.定义
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w’x+e,e为误差服从均值为0的正态分布。
X:输入变量
y:目标变量
希望找到一个映射使得 F : X − > y F: X -> y F:X−>y,

3.线性回归特点:
- 1.两个连续变量正常的散点图呈现云状;
- 2.一条穿过这些点中间的直线可以使得方差的和最小,并用其去描述某种趋势;
- 3.至少从理论上来说,当X向更高或者更低的值延续时,Y也如此;同一条直线在X值较大时可以预测对应的Y值,也可以在X值较小时预测对应的Y值
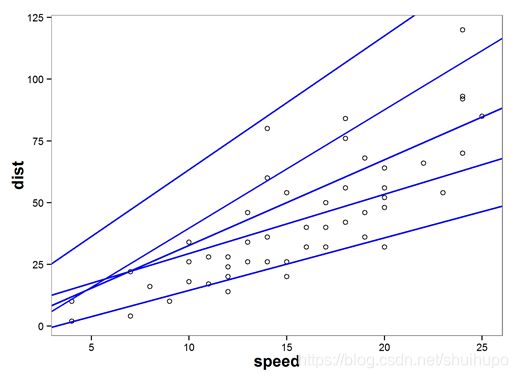
如何才能选择到最合适的直线去拟合数据呢?以下几条直线都在拟合数据,哪一条更好呢?这时需要引入损失函数来衡量各个模型。
线性回归损失函数
线性回归使用平方损失函数:
L ( Y , f ( X ) ) = ( Y − f ( X ) ) 2 L(Y,f(X))= (Y-f(X))^2 L(Y,f(X))=(Y−f(X))2。残差,是指真是值与预测值的差值,残差平方和越小等价于预测值与真实值的差异越小,对于线性回归模型来说平方损失也等价于残差平方,线性回归通过最小化残差平方和,选取最合适的模型参数。目标函数为:
m i n ( S S E ) min(SSE) min(SSE),
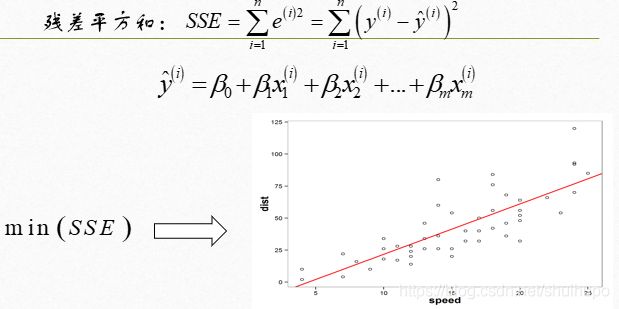
进行简单的改写
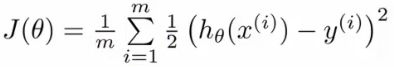
求解参数方法可使用最小二乘法求解参数,其原理也是最小化残差平方和。
高斯-马尔可夫定理
在误差零均值,同方差,且互不相关的线性回归模型中,由最小二乘估计得出的回归系数是所有估计中的最佳线性无偏估计(BLUE)
线性回归的评估指标
残差估计
线性回归法的指标MSE, RMSE,MAE和R Square
SSE(误差平方和)
同样的数据集的情况下,SSE越小,误差越小,模型效果越好
缺点:
SSE数值大小本身没有意义,随着样本增加,SSE必然增加,也就是说,不同的数据集的情况下,SSE比较没有意义。
MSE (Mean Squared Error)叫做均方误差。也是线性回归的损失函数。
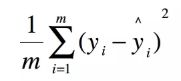
RMSE(Root Mean Squard Error)均方根误差。
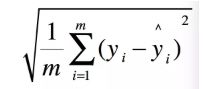
这个和均方误差本质一样的,不同点就体现在解释上,平方后的单位显得不那么好解释。
R-square(决定系数)

分母理解为原始数据的离散程度,分子为预测数据和原始数据的误差,二者相除可以消除原始数据离散程度的影响。
其实“决定系数”是通过数据的变化来表征一个拟合的好坏。
理论上取值范围(-∞,1], 正常取值范围为[0 1] ------实际操作中通常会选择拟合较好的曲线计算R²,因此很少出现-∞
越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好
越接近0,表明模型拟合的越差
经验值:>0.4, 拟合效果好
缺点:
数据集的样本越大,R²越大,因此,不同数据集的模型结果比较会有一定的误差
原文:https://blog.csdn.net/shy19890510/article/details/79375062
关于拟合优度可参考
Adjusted R-Square (校正决定系数)
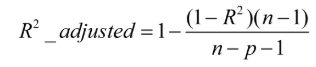
n为样本数量,p为特征数量
消除了样本数量和特征数量的影响
优化方法(梯度下降法、牛顿法、拟牛顿法等)
统计学习方法 附录 篇217页
梯度下降法
梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。
牛顿法
简单来说是为了求最值,而在可导的情况下,最值存在于在导数为零的点,牛顿法就是一种求导数=0点的算法。 牛顿法和拟牛顿法是求解无约束最优化问题的常用方法,它们比梯度下降收敛更快。考虑同样的一个无约束最优化问题:
sklearn参数详解
#切割数据集
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
#导入
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train, y_train)
#拟合完毕后,我们看看我们的需要的模型系数结果:
#LinearRegression将方程分为两个部分存放,coef_存放回归系数,intercept_则存放截距,因此要查看方程,就是查看这两个变量的取值。
print(linreg.intercept_)
print (linreg.coef_)