图形学初步---------直线生成算法DDA
近来偶然的需要,学习了一下图形学的基础。下面记录一下关于直线生成算法DDA的理解。
基础知识:
在计算机中,直线的显示并不是连续的,而是离散的点,这是由光栅化的本质决定的。
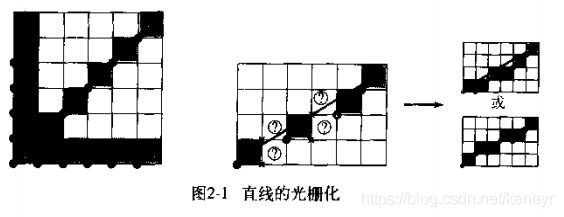
我们可以把屏幕理解为阴极射线管光栅显示器,这个显示器是由离散可发光的有线区域单元(像素)组成的矩阵。确定最佳逼近某直线的像素的过程通常叫做光栅化。对于水平线、垂直线以及45°线,选择哪些光栅元素是显而易见的,而对于其他方向的直线,像素的选择就很困难。如下图,对于中间的那幅图而言,我们不知道问号区域到底是上面填充颜色还是下面填充颜色:
那么一个画线算法需要满足哪些要求呢?
1.直线应该外观笔直,且具有最精确的起点和终点
2.直线的亮度应该保持不变,且与直线的长度和方向无关
3.直线的生成速度要快
但是事实上,只有水平线、垂直线、和45°线的亮度可以保持不变,其他的直线产生的都是不均匀的亮度。其实,水平线和垂直线的亮度是比45°线还要亮的,因为45°线上像素的有效间距大于垂直线和水平线的间距。
一般情况下,直线算法都是采用折中方法------只计算直线长度的近似值,采用整数运算将计算量减到最小,并用增量方法来简化运算。
DDA算法是直线算法里最为简单的算法,它的基本思想是高数里的微分算法,这里我直接截取书上的原图:
x1,y1、x2,y2是直线的端点坐标,yi是直线上某一步的初值。简单的DDA选择max(∆x,∆y)作为一个光栅单位。以下是伪代码:
-------------------------------------------------------------------------------------------------------
#approximate the line Length:获取直线长度
if abs(x2-x1)>=abs(y2-y1) then
Length = abs(x2-x1)
else
Length = abs(y2-y1)
end if
--------------------------------------------------------------------------------------------------------
#select the larger of delta_x or delta_y to be one raster unit:选择delta_x 和delta_y#的最大值作为一个光栅单元
delta_x = (x2-x1)/Length
delta_y = (y2-y1)/Length
--------------------------------------------------------------------------------------------------------
#round the values rather than trucate,so that center pixel
#addressing is handled correctly:对求出的x、y值加上0.5以后进行四舍五入,并且四舍五入的规则#符合:
#Integer(-8.5) = -9,而不是-8
x = x1 + 0.5
y = y1 + 0.5
--------------------------------------------------------------------------------------------------------
#begin main loop:开始循环
i = 1
while(i<=Length)
setpixel(Integer(x),Integer(y))
x = x+delta_x
y = y+delta_y
i = i + 1
end while
finish
-------------------------------------------------------------------------------------------------------可能看完伪代码之后,还是会一头雾水,不知道具体的生成过程是什么样的。下面就以两个例子来讲解这个伪代码,看完例子你一定会恍然大悟啦。
例1. 在第一象限,画出从(0,0)到(5,5)的直线段
#初始值:
x1 = 0,y1 = 0
x2 = 5,y2 = 5
#loop之前
Length = 5
delta_x = 1,delta_y = 1
x = 0.5,y = 0.5
i = 1
#loop
Step1:
setpixel(0,0)
x = 1.5,y = 1.5
i = 2
Step2:
setpixel(1,1)
x = 2.5,y = 2.5
i = 3
Step3:
setpixel(2,2)
x = 3.5,y = 3.5
i = 4
Step4:
setpixel(3,3)
x = 4.5,y = 4.5
i = 5
Step5:
setpixel(4,4)
x = 5.5,y = 5.5
i = 6
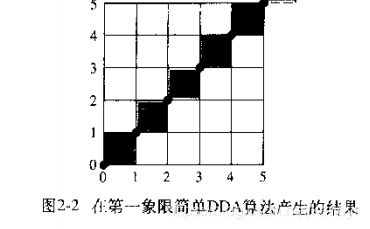
#跳出loop因此这个画图的结果是这样的:
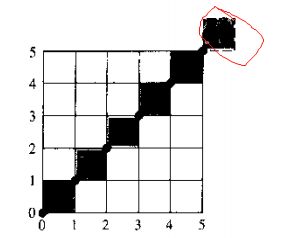
我们可以看到,端点(0,0)是显示的,但是端点(5,5)没有显示,我把这个setpixel(x,y)理解为描(x,y)右上角的正方形。为什么要让(5,5)不显示呢,因为如果端点(5,5)也描上去的话,程序里的i就应该从0开始。当下一条线段的起始段是(5,5)的时候,就会和这条线段重合一个像素点,会导致(5,5)这个像素点更亮,如下。
例2.在第三象限从(0,0)到(-8,-4)画一条线段
#初始值:
x1 = 0,y1 = 0
x2 = -8,y2 = -4
#loop之前
Length = 8
delta_x = -1
delta_y = -0.5
x = 0.5,y = 0.5
i = 1
#loop
Step1:
setpixel(0,0)
x = -0.5,y = 0
i = 2
Step2:
setpixel(-1,0)
x = -1.5,y = -0.5
i = 3
Step3:
setpixel(-2,-1)
x = -2.5,y = -1.0
i = 4
Step4:
setpixel(-3,-1)
x = -3.5,y = -1.5
i = 5
Step5:
setpixel(-4,-2)
x = -4.5,y = -2.0
i = 6
Step6:
setpixel(-5,-2)
x = -5.5,y = -2.5
i = 7
Step7:
setpixel(-6,-3)
x = -6.5,y = -3.0
i = 8
Step8:
setpixel(-7,-3)
x = -7.5,y = -3.5
i = 9
#跳出loop因此画图的结果是这样的:
所以这时候的setpixel(x,y)就是描的(x,y)左下角的小正方形。
这时候基本c++的代码就能写出来啦。写代码的时候,我们也能看到,最重要的是变量的类型,到底是int,还是double,还是什么?这些都是最基本的c++常识,暂不多说,code如下:
void CCGPainterView::DrawLine(CDC *pDC, CPoint ptStartPoint, CPoint ptEndPoint, COLORREF cLineColor)
{
// pDC->MoveTo(ptStartPoint);
// pDC->LineTo(ptEndPoint);
/*************************************************************
write the Bresenham' line algorithm for drawing the line
use function: pDC->SetPixelV(point, cLineColor); to drawing a pixel
编码直线生成算法,调用函数pDC->SetPixelV(point, cLineColor)画像素。
*************************************************************/
CPoint point;
float x0 = ptStartPoint.x,y0 = ptStartPoint.y;
float x1 = ptEndPoint.x,y1 = ptEndPoint.y;
float x,y;
int len = max(abs(x1 - x0), abs(y1 - y0));
float delt_x = (x1 - x0) / len;
float delt_y = (y1 - y0) / len;
x = x0 + 0.5;
y = y0 + 0.5;
int i = 1;
while (i <= len){
point.x = x, point.y = y;
pDC->SetPixelV(point, cLineColor);
x = x + delt_x;
y = y + delt_y;
i++;
}
}我这里只是填充了一个画线函数,整个框架的代码太多,就不放在页面上了。待我了解的更深入以后,会一并放在github上。github链接写在评论里。运行的结果如下:
仔细观察你会发现,只有垂直和水平的线看起来是连续的毫无缝隙的,但是有斜率的线都是离散的,并没有那么光滑。之后我们还会讲另外的更加优化的算法。
萌新报道,若有技术性错误,还请各位大佬指正喲~
笔芯~