关于AB test的一些整理
AB test的作用及流程
A/B test 是一种将网页或应用程序的两个或多个版本随机显示给不同组用户,通过统计分析方法确定哪个版本的指标性能更好的一种实验方法。
举个栗子:
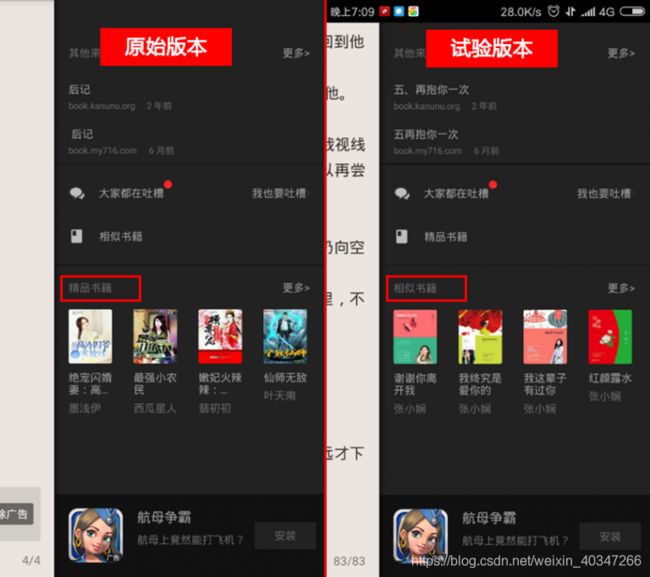
某读书软件的书籍推荐页有两种推荐方式可以实行,至于哪种推荐方式能带来更多的阅读量和追新量,就需要借助A/B测试来找到更好的推荐方法。
原始版本:主推“精品书籍”版块,即当下优质书目推荐,与用户阅读的书籍类型无关;
试验版本:主推“相似书籍”版块,即根据用户当前阅读的书籍类型,推荐与之相似的其他书目。
流程:
1. 收集指标,建立指标体系
首先要确定用于判断新版本是否比原始版本更成功的指标,比如在上面的案例中可以将“展示书籍点击量、更多选项点击量、添加到书架点击量、开始阅读点击量”作为本次试验的核心优化指标,同时设定“总消费金额”为辅助观察指标。
2. 分配流量,AB实验
实验抽样很可能出现抽样不均的情况,尽量采用科学的试验流量分割,使得每一组试验对象具备一致的用户特征,保证实验数据的变化仅仅是实验本身引起的。可以一次性抽取4/5组流量,选择任意两组不加策略空跑,监控核心指标数据,选取两组数据最为接近的上实验。
3. 假设检验
(1)确定实验周期(一般7天),可以通过用户使用频率来判断产品周期
(2)确定实验所需样本量
太多会浪费资源,太少会因为统计灵敏度太低而得到不显著的结论
理论上样本量越多越好,但工作中是越少越好…一方面流量有限(大公司这点倒是不愁),另一方面试错成本高,想想假如我们拿50%的用户来跑实验,但不幸的是,1周后结果表明实验组的总收入下降了20%。算下来,你的实验在一周内给整个公司带来了10%的损失。这个试错成本未免高了一些…
网上也有类似的 sample size 计算器,计算公式如下:
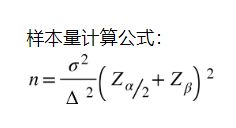
其中 n 是每组所需样本量,因为A/B测试一般至少2组,所以实验所需样本量为 2n;Z为正态分布的分位数函数;Δ为两组数值的差异,如点击率1%到1.5%,那么Δ就是0.5%;σ为标准差,是数值波动性的衡量,σ越大表示数值波动越厉害。
第一类错误 α:弃真错误,原假设H0为真但是拒绝了H0(这里可以理解为原来的版本效果更好但是却被撤下了)
第二类错误 β:取伪错误,原假设H0为非真但接受了H0(可以理解为原版本效果不好但是没有被实验发现而是仍然保留下来)
α一般可取5%,β一般可取20%,对两类错误上限的选取,我们可以了解到A/B实验的重要理念:宁肯砍掉4个好的产品,也不应该让1个不好的产品上线。
(3)配对样本T检验
由于总体参数标准差未知,因此一般使用T检验。而配对T检验就适用于“两种同质对象分别接受两种不同的处理,判断不同的处理是否有差别”。
设实验组、对照组有n天数据,
X = ( X 1 , X 2 , . . . . . , X n ) X = (X_1, X_2, .....,X_n ) X=(X1,X2,.....,Xn) Y = ( Y 1 , Y 2 , . . . . . , Y n ) Y = (Y_1, Y_2, .....,Y_n ) Y=(Y1,Y2,.....,Yn)
做配对T检验,令 Z = ( Z 1 , Z 2 , . . . . . , Z n ) Z = (Z_1,Z_2, .....,Z_n ) Z=(Z1,Z2,.....,Zn)
其中,
Z i = X i − Y i , i = 1 , 2 , . . . , n Z_i = X_i - Y_i, i= 1,2,...,n Zi=Xi−Yi,i=1,2,...,n
设
H 0 : μ = 0 H_0:\mu = 0 H0:μ=0 H 1 : μ ≠ 0 H_1:\mu \not= 0 H1:μ=0
有T统计量
T = n ∗ Z ‾ S z ∼ t ( n − 1 ) T = \frac {\sqrt{n} * \overline{Z}} {S_z} \sim t(n-1) T=Szn∗Z∼t(n−1)
拒绝域
W = P ( ∣ T ∣ > = t 1 − α 2 ( n − 1 ) ) W = P(|T| >= {t_ {1 - \frac {\alpha}{2}}(n-1)}) W=P(∣T∣>=t1−2α(n−1))
P值:
p = 2 t n − 1 ( ∣ T ∣ ) p = 2t_{n-1}(|T|) p=2tn−1(∣T∣)
要更小的P值才能拒绝原假设H0。会使一类错误概率降低,二类错误概率提高。要使二类错误概率不过高,可以通过增加样本量来解决。
如果主要观测指标是转化率或者CTR这些比例,则需要使用二项分布。
使用A方案的样本量 N A N_A NA,使用B方案的样本量 N B N_B NB,通常情况下 N A = N B = N N_A = N_B = N NA=NB=N
由样本计算出A方案的转化率为 P a ^ \hat{P_a} Pa^,B方案的转化率为 P b ^ \hat{P_b} Pb^,
总体A的分布为 A ∼ B ( N , P a ) A \sim B(N, P_a) A∼B(N,Pa), B ∼ B ( N , P b ) B \sim B(N, P_b) B∼B(N,Pb),
根据中心极限定理可知, P a ^ \hat{P_a} Pa^ 和 P b ^ \hat{P_b} Pb^ 近似服从正态分布:
P a ^ ∼ N ( P a , P a ^ ( 1 − P a ^ ) / N ) \hat{P_a} \sim N(P_a, \hat{P_a}(1-\hat{P_a})/N) Pa^∼N(Pa,Pa^(1−Pa^)/N), P b ^ ∼ N ( P b , P b ^ ( 1 − P b ^ ) / N ) \hat{P_b} \sim N(P_b, \hat{P_b}(1-\hat{P_b})/N) Pb^∼N(Pb,Pb^(1−Pb^)/N)
所以根据正态分布的性质:
X = P b ^ − P a ^ ∼ N ( P b − P a , P b ^ ( 1 − P b ^ ) N + P a ^ ( 1 − P a ^ ) N ) X = \hat{P_b} - \hat{P_a} \sim N(P_b - P_a, \frac{\hat{P_b}(1-\hat{P_b})}{N} + \frac{\hat{P_a}(1-\hat{P_a})}{N}) X=Pb^−Pa^∼N(Pb−Pa,NPb^(1−Pb^)+NPa^(1−Pa^))
由于我们的期望结果是B方案的转化率高于A方案的转化率,所以原假设和备择假设如下:
H 0 : X = P b − P a ≤ 0 H_0: X = {P_b} -{P_a} \leq 0 H0:X=Pb−Pa≤0 H 1 : X = P b − P a > 0 H_1:X = {P_b} - {P_a} > 0 H1:X=Pb−Pa>0
构建检验统计量:
Z = P b ^ − P a ^ P b ^ ( 1 − P b ^ ) N + P a ^ ( 1 − P a ^ ) N Z = \frac{\hat{P_b} - \hat{P_a}}{\sqrt{\frac{\hat{P_b}(1-\hat{P_b})}{N} + \frac{\hat{P_a}(1-\hat{P_a})}{N}}} Z=NPb^(1−Pb^)+NPa^(1−Pa^)Pb^−Pa^
给定显著性水平为 α。当 Z > Z α Z > Z_α Z>Zα 时,拒绝原假设,认为B方案所带来的转化率高于A方案所带来的转化率,建议可以进行推广;当 Z ≤ Z α Z \leq Z_α Z≤Zα时,不能拒绝原假设,即认为B方案所带来的转化率不高于A方案所带来的转化率,建议暂不建议进行推广。
4 . 决策方案
结论可能有:正收益、负收益、持平
(1)正收益:
本次页面改进在显著性水平内,证明了“转化率提升”的假设。并且收益提升率达到预期水平。
进一步验证实验是否正确—实验反转
当得出实验正向结论后,将实验反转,对照组变成实验组,实验组变成对照组。 原因:反转实验能够验证实验数据的差别是由实验本事引起的。但需要注意的是,建议只在实验为正向收益时反转实验。如果收益为负,反转实验,只会多损伤原对照组的用户体验。
具体做法:举个例子,实验目的为“按钮大小对该按钮点击率的影响”。A 组流量按钮变⼤,B 组为对照 组,按钮⼤⼩正常,数据显示A组的按钮点击率升高,效果更好。在反转试验中,A 组流量按钮恢复正常,B 组变为实验组,按钮变大。如果此时数据显示B组按钮点击率升高,说明按钮大小对点击率有影响。
(2)负收益:优化迭代方案重新开发本次页面改进。在显著性水平内,核心指标负向变化显著。
(3)持平:调整分流比例继续测试
1.本次页面改进在显著性水平内,无法证明‘转化率提升的假设’。分析原因可能是新版本样本空间不足。2.产品变化本身收益不明显
python 实现A/B test的案例:
利用 python 中的 scipy.stats.ttest_ind 做关于两组数据的双边 t 检验,结果比较简单。但是做大于或者小于的单边检测的时候需要做一些处理,才能得到正确的结果。
from scipy import stats
import numpy as np
import seaborn as sns
# 两组示例实验数据
A = np.array([ 1, 4, 2, 3, 5, 5, 5, 7, 8, 9,10,18])
B = np.array([ 1, 2, 5, 6, 8, 10, 13, 14, 17, 20,13,8])
print('策略A的均值是:',np.mean(A))
print('策略B的均值是:',np.mean(B))
Output:
策略A的均值是:6.416666666666667
策略B的均值是:9.75
很明显,策略B的均值大于策略A的均值,但这就能说明策略B可以带来更多的业务转化吗?还是说仅仅是由于一些随机的因素造成的。
我们是想证明新开发的策略B效果更好,所以可以设置原假设和备择假设分别是:
H0:A>=B
H1:A < B
scipy.stats.ttest_ind(x,y)默认验证的是 X.mean()-Y.mean() 这个假设。为了在结果中得到正数,计算如下:
stats.ttest_ind(B,A,equal_var= False)
根据 scipy.stats.ttest_ind(x, y) 文档的解释,这是双边检验的结果。为了得到单边检验的结果,需要将 计算出来的 p value 除于2 取单边的结果(这里取阈值为0.05)。
求得pvalue=0.13462981561745652,p/2 > alpha(0.05),所以不能够拒绝假设,所以暂时不能够认为策略B能带来多的用户点击。
AB test如何处理多个实验并行的相互影响
假如线上同时进行多个实验,比如电商的购物流程中同时对搜索排序算法和商品详情页UI进行优化,这两个变动贯穿于用户购物流程中,相互之间可能有影响,我们需要区分实验中这两种改动带来的影响分别是怎样的
流量分层是把线上流量划分成N个100%的流量层,实验可能会分配到任⼀一流量层中, 流量层的基本原则是位于同层的实验中流量互斥,位于不同层的实验可能会被同一流量命中。
正交实验:每个独立实验为一层,层与层之间流量是正交的,一份流量穿越每层实验时,都会再次随机打散。
不同业务类型实验可以在不同层实验,如果不同层实验基本上没有任何的业务关联度的,即使共用相同的流量 ( 流量正交 ) 也不会对实际的业务造成结果。同一类型实验在同一层进行。
参考链接:
https://zhuanlan.zhihu.com/p/20680232
https://zhuanlan.zhihu.com/p/116002163
https://mp.weixin.qq.com/s/O6yt4cKdvRG6hxufaG-PnA
https://zhuanlan.zhihu.com/p/40919260
https://blog.csdn.net/buracag_mc/article/details/74905483
https://jeffshow.com/caculate-abtest-required-sample-size.html