Routh-Hurwitz准则——判别实系数多项式有无实部非负的根的充要条件

本文为 该知乎文章搬运到CSDN的文章， 该文章作者与本文章为同一人，内容是本人原创。之所以搬运到CSDN，是因为CSDN的markdown编辑器比较好用，最关键的是文章超链接功能，因为我写的文章都比较长，没有超链接找起来很辛苦。从今往后我将经常在CSDN发文， 有时候会把部分我在知乎写的文章搬运过来。因为知乎的编辑器与CSDN的编辑器不同，所以搬运也比较麻烦，所以不定期更新。 本文在原文上有一些增补修改（增加了第三章的4、5），修改了部分错误，增加了Routh-Hurwitz准则在特殊情况下的处理方式。本文 从证明思路、细节的角度讲解Routh-Hurwitz准则，对具体应用也有一定阐述。

Routh-Hurwitz准则（R-H准则）是一个「判别系统稳定性」的重要准则，它给出了一个「判别实系数多项式有无实部非负的根」的充要条件。遗憾的是，笔者在学习这一准则时，并未在网上发现其他作者对该准则进行梳理，更没有找到该准则的证明过程（书上也未给出证明）。因此，笔者在梳理相关参考文献基础上，结合笔者自己的理解，简化了部分参考文献的思路，对该准则进行了证明和梳理。

一、引言

在系统分析中，我们往往关注系统的频率特性，即系统响应函数 h(t) 的拉普拉斯变换函数 H(s) 。常见的 H(s) 往往是「多项式除以多项式」型的，即分子分母都是实系数多项式。我们期望我们的系统是一个稳定的系统，即有界输入对应有界输出（BIBO）。而我们知道：「系统的稳定性问题」等价于「系统函数 H(s) 的极点 p_k 是否在左半平面¹」。而R-H准则给了我们判别之的一个充要条件 。至于这个充要条件具体是什么，请读者继续看后文内容。

举一个简单的例子： $H(s)=\frac{s^2+3s+3}{s^3+3s^2+4s+2}=\frac{1}{s+1}+\frac{1}{s^2+2s+2}$，这个信号对应的时域响应（拉普拉斯反变换）为 $f(t)={\mathrm{e}}^{-t}+{\mathrm{e}}^{-t}\sin t$ ，因为有一个「指数衰减因子」 ${\mathrm{e}}^{-t}$，这个信号自然衰减得很快。因此，这个系统是一个稳定系统。

而我们注意到， H(s) 的极点的实部均为-1，这也是 f(t) 的「指数衰减因子」 ${\mathrm{e}}^{-1\cdot t}$ 为-1的原因。推而广之，极点的实部充分必要地决定了其拉普拉斯反变换函数的「指数衰减因子」的系数，这也自然充分必要地决定了系统地稳定性。

而极点的实部判别又可以充分必要地通过「R-H准则」进行，这也是「R-H准则」的实际应用所在。

二、准则内容

对于一个多项式 $p(s)=a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0$

不妨设 $a_n>0$ ，接下来，让我们构造一个被称为「Rouch表」的东西，我们可以断言——「多项式 $p(s)$ 所有零点都位于左半平面」等价于「Rouch表首列元素都为正」（如果不是，那么符号改变的次数即为右半平面根的个数）。

为了便于实际应用，在这里我将「Rouch表」进行了一个变形 。在后续证明过程中，我们使用的是另一种形式的「Rouch表」，我们只需要知道它们两个是一个东西就行了。

①如果n为偶数，则我们称下表为 $p(s)$ 的Rouch表
$$\begin{array}{lllclll}{a}_n& a_{n-2}& a_{n-4}& \cdots & a_4& a_2& a_0\\ a_{n-1}& a_{n-3}& a_{n-5}& \cdots & a_3& a_1& a_{-1}\\ c_{n-1}& c_{n-3}& c_{n-5}& \cdots & c_3& c_1& \\ d_{n-1}& d_{n-3}& d_{n-5}& \cdots & d_3& d_1& \\ ⋮& & & & & & \\ u_{n-1}& u_{n-3}& & & & & \\ u_{n-1}& u_{n-3}& & & & & \\ v_{n-1}& & & & & & \end{array}\}n+1行\text{\hspace{1em}(2.1)}$$

其中 $a_n,a_{n-1},\cdots ,a_1,a_0$ 与多项式 $p(s)$ 系数相同， $a_{-1}$ 为人为补的0。
并且系数有（其余以此类推）：

$c_{n-1}=\frac{-\left|\begin{array}{ll}{a}_n& a_{n-2}\\ a_{n-1}& a_{n-3}\end{array}\right|}{a_{n-1}}$ ， $c_{n-3}=\frac{-\left|\begin{array}{ll}{a}_n& a_{n-4}\\ a_{n-1}& a_{n-5}\end{array}\right|}{a_{n-1}}$
$d_{n-1}=\frac{-\left|\begin{array}{ll}{a}_{n-1}& a_{n-3}\\ c_{n-1}& c_{n-3}\end{array}\right|}{c_{n-1}}$ ， $d_{n-3}=\frac{-\left|\begin{array}{ll}{a}_{n-1}& a_{n-5}\\ c_{n-1}& c_{n-5}\end{array}\right|}{c_{n-1}}$

②如果n为奇数，则我们称下表为 $p(s)$ 的Rouch表
$$\begin{array}{lllcllll}{a}_n& a_{n-2}& a_{n-4}& \cdots & a_5& a_3& a_1& a_{-1}\\ a_{n-1}& a_{n-3}& a_{n-5}& \cdots & a_4& a_2& a_0& a_{-2}\\ c_{n-1}& c_{n-3}& c_{n-5}& \cdots & c_4& c_2& c_0& \\ d_{n-1}& d_{n-3}& d_{n-5}& \cdots & d_4& d_2& d_0& \\ ⋮& & & & & & & \\ u_{n-1}& u_{n-3}& & & & & & \\ u_{n-1}& u_{n-3}& & & & & & \end{array}\}n+1行\text{\hspace{1em}(2.2)}$$
除了 $a_{-1}$,$a_{-2}=0$ 进行补0以外，其余系数关系与n为偶数情形是相一致的。

三、举例说明

前面的内容较为抽象，下面举几个具体例子，让大家直观感受一下「R-H准则」的使用方式。

1、设某系统的系统函数为 $H(s)=\frac{A{s}^2+Bs+C}{s^3+s^2+2s+8}$ （A、B、C均为实常数），用「R-H准则」判断该系统是否稳定。
解：
显然：「系统稳定」等价于「 H(s) 极点全在左半平面」等价于「分母多项式零点全位于左半平面」，故对分母多项式采用「R-H准则」判别。
列出「Rouch表」如下：
$\begin{array}{rrr}1& 2& 0\\ 1& 8& 0\\ -6& 0& \\ 8& 0& \end{array}$
显然，「Rouch表」第一列元素为 $1\to 1\to -6\to 8$ ，有两次改变符号，则分母多项式有两个右半平面零点，显然系统不稳定。

2、判别多项式 $f(x)=x^4+2x^3+3x^2+4x+5$ 的零点分布情况
解：
列出「Rouch表」如下：
$\begin{array}{rrrc}1& 3& 5& 0\\ 2& 4& 0& 0\\ 1& 5& 0& \\ -6& 0& 0& \\ 5& 0& & \end{array}$
显然，「Rouch表」第一列元素为 $1\to 2\to 1\to -6\to 5$ ，有两次改变符号，则多项式有两个右半平面零点。

3、判别多项式 $f(x)=x^3+2x^2+2x+1$ 的零点分布情况
解：
列出「Rouch表」如下：
$\begin{array}{ccc}1& 2& 0\\ 2& 1& 0\\ \frac{3}{2}& 0& \\ 1& 0& \end{array}$
显然，「Rouch表」第一列元素为 $1\to 2\to \frac{3}{2}\to 1$ ，未改变符号，则多项式零点全在左半平面。

特殊情况1：某行出现分母为0
解决方案：把f(x)乘以(x+1)
4、判别多项式 $f(x)=x^3+2x+1$ 的零点分布情况
先列出Routh表前2行：
$\begin{array}{ccc}1& 2& 0\\ 0& 1& 0\end{array}$
注意到：3行1列出现分母为0，Routh准则失效
为了解决这一问题，采用一个技巧：把f(x)乘以(x+1)
即：构造出$g(x)=(x+1)(x^3+2x+1)=x^4+x^3+2x^2+3x+1$
解：
列出「Rouch表」如下：
$$\begin{array}{rrrc}1& 2& 1& 0\\ 1& 3& 0& 0\\ -1& -1& 0& \\ 2& 0& 0& \\ 1& 0& & \end{array}$$
显然，「Rouch表」第一列元素为 $1\to 1\to -1\to 2\to 1$ ，有两次改变符号，则多项式有两个右半平面零点。

特殊情况2：出现全零行
解决方案：构造偶次多项式
5、判别多项式 $f(x)=x^6+x^5-2x^4-3x^3-7x^2-4x-4$ 的零点分布情况
解：
列出「Rouch表」如下：
$\begin{array}{ccrrrc}{s}^6& 1& -2& -7& -4& 0\\ s^5& 1& -3& -4& 0& 0\\ s^4& 1& -3& -4& 0& \\ s^3& 0& 0& 0& 0& \end{array}$
注意到：$s^3$行出现全零行
解决方案：用$s^4$的系数构造偶次多项式（原因是Routh判据的证明方式就是借助的偶次多项式）
利用$s^4$的系数构造$F(s)=s^4-3s^2-4$
求导得到$F^{\prime }(s)=4s^3-6s$
续写Routh表：
$\begin{array}{ccrrrc}{s}^6& 1& -2& -7& -4& 0\\ s^5& 1& -3& -4& 0& 0\\ s^4& 1& -3& -4& 0& \\ s^3& 4& -6& 0& & \\ s^2& -1.5& -4& 0& & \\ s^1& -\frac{100}{3}& 0& & & \\ s^0& -4& 0& & & \end{array}$

事实上，只要出现全零行，我们构造偶次多项式的时候，我们就不必继续算下去了，因为必然会有不稳定根。这是因为在偶次多项式中令$t=s^2$，无论解出来t为何值，s的两根总是关于原点对称的。只要有一个左半平面根，另一根就必然是有右半平面的。事实上，本方程有1个右半平面根$x=2$与2个虚轴根$x=\pm j$。这也与Routh表变号一次这一事实相对应。不过在这里虚轴根没有被算在不稳定根里面，所以遇到全零行这种情况，大可直接说系统不稳定就好了

四、证明思路

这一准则的证明是相对复杂的，如果不在此之前理清证明的思路，我们恐怕是难以看懂证明的。事实上，由于参考文献的许多处（不下于10处）书写错误，以及笔者自身能力的菜，导致这个证明啃了很长时间。在理清参考文献的大致思路后，笔者决定换一个更清晰的角度来证明这一准则。这一证明力图向读者展现证明的思路，为了保证其思路的清晰性，会损害一些严谨性。但是，这种直观分析方法有助于让读者理解这一证明中的核心思想。

思路：
在提到多项式在全复平面的零点，我们第一想到的必然是「代数基本定理」。而第二想到的，则应当是《复变函数》里面的「辐角原理」。不过遗憾的是，这个内容很多学校没有讲，甚至我们教材上也没有这个内容，我也是在高等教育出版社的《复变函数》中才学到这一内容 的。因此，在证明之前，我觉得应当有必要说一说「辐角原理」。

「辐角原理」：若f(z)在封闭区域 C 的边界与内部解析，且在边界上无零点，则有：

C内部的零点数=$\frac{1}{2\pi }\times$(沿C巡行一周辐角改变量)

辐角原理用「辐角」改变量刻画了「 f(z) 在区域内的零点数」。在这一问题中，我们的思路核心就是就是利用辐角原理转化问题。

总体思路：
如下图所示：取 $R\to \infty$ 的半圆围道C，并且用绕开全部虚轴零点的直线C1、C2连接之，其中P1、P2为虚轴零点，P3、P4、P5为左半平面零点。不妨记 $C_0=C+C_1+C_2$ 。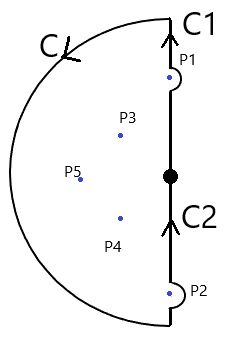
我们试图使用“筛”的方法，记原多项式为 $p_n(x)$ ，构造一族辅助多项式 $\{p_n(s)\}$ ，分别为n次、n-1次、…、1次、0次，由于「代数基本定理」，我们容易知道这一族辅助多项式 $\{p_n(s)\}$ 中每个多项式的总零点数分别为n个、n-1个、…、1个、0个。那么，我们期望能找到一个充要的手段，使得：这族辅助多项式每次减少的一个零点都在左半平面。这样的话，我们就可以“筛”出n个左半平面的零点。反之，如果不能筛出n个左半平面的零点，由于这个办法是充要的，就可以说明左半平面确实没有n个零点。

那么，如何“筛”呢？根据「辐角原理」，我们知道：区域 $C_0$ 内每减少一个零点，辐角改变量减少2π。从这里入手，如果能找到一种“筛”的法则，使得每次都能减少且仅减少2π个辐角改变量，那么这个法则就能充要的判别该多项式是否只有左半平面零点。

当然，值得补充的是，巡行路径 $C_0$ 对于多项式族 $\{p_n(s)\}$ 是不能变的。C倒没什么问题，因为 $R\to \infty$ 这一点足以让其绕过所有零点。但虚轴上的零点P1、P2则是无法绕过的。所以，我们还期望这种“筛”的法则能够让辅助多项式族 $\{p_n(s)\}$ 在虚轴上的零点总是不变的。

好了，以上就是证明的思路梗概，接下来就是利用这个思路进行具体的证明了。

如果不想看繁琐的证明的读者，只想知道思路梗概的话，请跳转到第六章

五、证明

再把之前的图贴过来，因为后面证明会大量用到这张图。

为了证明看着方便，将Rouch表进行一些改造：
$$\begin{array}{clllclllc}行数& & & & \text{Rouch}表& & & & 辅助多项式\\ 1& a_n& a_{n-2}& a_{n-4}& \cdots & a_4& a_2& a_0& h_n(s^2)\\ 2& a_{n-1}& a_{n-3}& a_{n-5}& \cdots & a_3& a_1& & g_{n-2}(s^2)\\ 3& b_{n-2}& b_{n-4}& b_{n-6}& \cdots & b_2& b_0& & h_{n-2}(s^2)\\ 4& b_{n-3}& b_{n-5}& b_{n-7}& \cdots & b_1& & & g_{n-4}(s^2)\\ ⋮& ⋮& & & & & & & ⋮\\ n-1& u_2& u_0& & & & & & h_2(s^2)\\ n& u_1& & & & & & & g_0(s^2)\\ n+1& v_0& & & & & & & h_0(s^2)\end{array}$$

并构造这一族辅助多项式：
$$\begin{array}{rlrl}{p}_n(s)& =h_n(s^2)& +& s{g}_{n-2}(s^2)\\ p_{n-1}(s)& =s{g}_{n-2}(s^2)& +& h_{n-2}(s^2)\\ p_{n-2}(s)& =h_{n-2}(s^2)& +& s{g}_{n-4}(s^2)\\ ⋮& & & \\ p_2(s)& =h_2(s^2)& +& s{g}_0(s^2)\\ p_1(s)& =s{g}_0(s^2)& +& h_0(s^2)\end{array}\}\text{\hspace{1em}(5.0.1)}$$

直观地看， g(s) 是原多项式的全体奇数次项除以s， h(s) 是原多项式的全体偶数项。

举个例子或许会更直观：
如果 $p_4(s)=s^4+2s^3+3s^2+4s+5$ ，
那么 $h_4(s^2)=s^4+3s^2+5，s{g}_2(s^2)=2s^3+4s$
也就是说 $g_2(s^2)=2s^2+4$

为了读者理解，此处的证明倾向于启发式，用直观的方法让读者感受准则为何成立

以下证明以n为偶数为例，n为奇数仿此证明不难。
先证明2个引理，之后的内容就水到渠成了。

引理1

引理1、辅助多项式族 $\{p_n(s)\}$ 在虚轴上的零点（包括重数）不变

原文献证明思路是用零点定义利用代数方法化简证明来做，笔者认为这不直观，笔者采取了一种直观的方法来分析这个问题。

分析：
假设虚轴上一点 $s=j\omega$ 是 $p_n(s)=a_n{s}^n+a_{n-1}{s}^n+\cdots +a_{1}s+a_0$ 的零点，那么自然有：
$$p_n(j\omega )=a_n(j\omega {)}^n+a_{n-1}(j\omega {)}^{n-1}+\cdots +a_1(j\omega )+a_0=0\text{\hspace{1em}(5.1.1)}$$
考虑到(5.0.1)，易见：
$$\{\begin{array}{llc}{p}_n(s)& =h_n(s^2)& +s{g}_{n-2}(s^2)\\ p_{n-1}(s)& =h_{n-2}(s^2)& +s{g}_{n-2}(s^2)\end{array}\text{\hspace{1em}(5.1.2)}$$
因为，我们这里只考虑虚轴上的零点，代入 $s=j\omega$ ：
$$\{\begin{array}{llc}{p}_n(j\omega )& =h_n(-{\omega }^2)& +j\omega g_{n-2}(-{\omega }^2)\\ p_{n-1}(j\omega )& =h_{n-2}(-{\omega }^2)& +j\omega g_{n-2}(-{\omega }^2)\end{array}\text{\hspace{1em}(5.1.3)}$$
由于h、g都是实系数多项式，那么 $h(-{\omega }^2)$ 自然是纯实数， $j\omega g(-{\omega }^2)$ 也自然是纯虚数。

也就是说：公式(5.1.3)相当于对 $p_n(x)$ 沿着实部和虚部进行拆分

回想一下，我们期望的是：多项式族 $\{p_n(s)\}$ 的虚轴共零点，依次左半平面零点数-1。

换言之，我们期望构造出一个 $u(s^2)$ ，使得$p_n(s)=p_{n-1}(s)+u(s^2)$ ，其中当s为 $p_n(s)$ 的零点或者 $p_{n-1}(s)$ 的零点时， $u(s^2)$ 总是为0。
这也就是我们如此构造系数 $b_{n-2}=\frac{-\left|\begin{array}{ll}{a}_n& a_{n-2}\\ a_{n-1}& a_{n-3}\end{array}\right|}{a_{n-1}}$ 的理由。

好了，让我们重回证明：

考虑到系数（其余同理不予列举，详见第二章） ：
$b_{n-2}=\frac{-\left|\begin{array}{ll}{a}_n& a_{n-2}\\ a_{n-1}& a_{n-3}\end{array}\right|}{a_{n-1}}=a_{n-2}-\frac{a_n{a}_{n-3}}{a_{n-1}}$

可以推出：
$$h_{n-2}(s^2)=b_{n-2}{s}^{n-2}+b_{n-4}{s}^{n-4}+\cdots +b_0=h_n(s^2)-\frac{a_n}{a_{n-1}}{s}^2{g}_{n-2}(s^2)\text{\hspace{1em}(5.1.4)}$$
将(5.1.3)两式相减：
$$p_n(s)=p_{n-1}(s)+\frac{a_n}{a_{n-1}}{s}^2{g}_{n-2}(s^2)\text{\hspace{1em}(5.1.5)}$$
我们注意到： $\frac{a_n}{a_{n-1}}{s}^2{g}_{n-2}(s^2)$ 就是我们要的 $u(s^2)$ 。

根据公式(5.1.2)，我们知道 $s{g}_{n-2}(s^2)$ 同时是 $p_n(s)$ 和 $p_{n-1}(s)$ 的虚部。无论是 $p_n(s)$ 为0，还是 $p_{n-1}(s)$ 为0，作为其虚部的 $s{g}_{n-2}(s^2)$ 必然为0，这也就证明了：$p_n(s)$ 与 $p_{n-1}(s)$ 在虚轴上共零点。故引理1得证。

事实上，我们还可以证明：不仅零点不变，而且零点重数也不变。此处留给读者作为习题（逃）。

引理2

引理2、如图，沿 $C_0=C+C_1+C_2$ 逆时针巡行一周， 则：$\Delta \mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-\Delta \mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=2\pi$ 的充要条件是 $a_n{a}_{n-1}>0$

分析：
将路径分解为C、C1、C2

①沿着C

设多项式为： $p_n(s)={\prod }_{i=1}^n(s-p_i)$

则：${\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)={\sum }_{i=1}^n{\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}(s-p_i)$

不失一般性地取一个 $\Delta \mathrm{A}\mathrm{r}\mathrm{g}(s-p_i)$ ，由于沿着C变动，如下图，我们试图说明：下图标示的角度总是180°。

看起来这一结论不可思议，因为从图上看起来它比180°大那么一点点。但事实上，如果我们稍加思索，便会发现其实显然成立的。因为 $R\to \infty$ ，无论你零点在哪里，在无穷大的半径面前，都一视同仁，蹦跶不起来。如果将这个圆想象得无穷大，那么我们可以显然得到 ${\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}(s-p_i)=\pi (\forall i)$ 。

即 ${\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)=n\pi$ ， ${\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=(n-1)\pi$

那么自然有(5.2.1)式成立：
$${\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_C\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\pi \text{\hspace{1em}(5.2.1)}$$

②沿着C1（C2同理，因为是对称的）

还是把图复制下来：

以及把公式(5.1.2)和(5.1.5)搬运下来：
$$\{\begin{array}{llc}{p}_n(s)& =h_n(s^2)& +s{g}_{n-2}(s^2)\\ p_{n-1}(s)& =h_{n-2}(s^2)& +s{g}_{n-2}(s^2)\end{array}\text{\hspace{1em}(5.1.2)}$$
$$p_n(s)=p_{n-1}(s)+\frac{a_n}{a_{n-1}}{s}^2{g}_{n-2}(s^2)\text{\hspace{1em}(5.1.5)}$$
前面提到：在虚轴上，h(s)是实部，sg(s²)是虚部。显然， $p_n(s)$ 与 $p_{n-1}(s)$ 的虚部相同。

将 $g_{n-2}(-{\omega }^2)$ 的全体零点如此排列： $0<{\omega }_1<{\omega }_2<\cdots <{\omega }_r<+\infty$ 。

在每个区间 $(0,{\omega }_1),({\omega }_1,{\omega }_2),\cdots ,({\omega }_{r-1},{\omega }_r)$ 上，由于 $g_{n-2}(-{\omega }^2)为p_n(j\omega ),p_{n-1}(j\omega )$ 的虚部，所以虚部符号不会改变。

并且由于 ${\omega }_i$ 是 $g(-{\omega }_i^2)$ 的零点，则 $p_n(j{\omega }_i)=p_{n-1}(j{\omega }_i)(i=1,2,\cdots ,r)$ 。

用通俗的话来总结上面这些分析，就是：以 $g_{n-2}(s^2)$ 的两个相邻虚轴零点作为起点和终点为路径， ${\Delta }_{C^{\prime }}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C^{\prime }}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=0$ ²

推而广之，沿着0到 $g_{n-2}(s)$ 的最大的一个零点 $j{\omega }_r$ 走，也有 ${\Delta }_{C^{\prime }}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C^{\prime }}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=0$ ，而且在 $s=j{\omega }_r$ 处有 $p_n(j{\omega }_r)=p_{n-1}(j{\omega }_r)$

再换句话说，就是：
$${\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(j\infty )-\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(j\infty )\text{\hspace{1em}(5.2.2)}$$
这么一看，就豁然开朗了！原来 $p_n$ 和 $p_{n-1}$ 在 $C_1$ 上的辐角变化只取决于 $j\infty$ 处的辐角差啊！

一涉及到无穷，我们一般就会很开心，因为这意味着低阶项我们都可以扔掉不管，只考虑最高阶的项，让我们来试试：
$${\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\mathrm{A}\mathrm{r}\mathrm{g}\frac{p_n(j\infty )}{p_{n-1}(j\infty )}=\mathrm{A}\mathrm{r}\mathrm{g}\frac{a_{n}j\omega }{a_{n-1}}$$
也就是说，辐角差取决于 $a_n$ 和 $a_{n-1}$ 是否同号，总结一下：
$${\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C_1}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\{\begin{array}{ll}\frac{\pi }{2},& \text{if}{a}_n{a}_{n-1}>0\\ -\frac{\pi }{2},& \text{if}{a}_n{a}_{n-1}<0\end{array}\text{\hspace{1em}(5.2.3)}$$
$${\Delta }_{C_2}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C_2}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\{\begin{array}{ll}\frac{\pi }{2},& \text{if}{a}_n{a}_{n-1}>0\\ -\frac{\pi }{2},& \text{if}{a}_n{a}_{n-1}<0\end{array}\text{\hspace{1em}(5.2.4)}$$
总结一下(5.2.1)、(5.2.3)、(5.2.4)：
$${\Delta }_{C_0}\mathrm{A}\mathrm{r}\mathrm{g}{p}_n(s)-{\Delta }_{C_0}\mathrm{A}\mathrm{r}\mathrm{g}{p}_{n-1}(s)=\{\begin{array}{ll}2\pi ,& \text{if}{a}_n{a}_{n-1}>0\\ 0,& \text{if}{a}_n{a}_{n-1}<0\end{array}\text{\hspace{1em}(5.2.5)}$$
考虑到(5.2.5)，根据辐角原理， p_{n-1} 比 p_n 减少一个左半平面零点，当且仅当 $a_n{a}_{n-1}>0$ ,故引理2得证。

结合引理1、2，原定理自然成立

六、证明思路梗概

我们注意到，证明的思路核心在于引理1、2，我们通过「辐角原理」将问题转化为 $C_0$ 围道的辐角问题，系数选择其实也是为了迎合「虚轴零点不变」、「公式(5.1.5)」。在确定好这些后，我们又注意到：C这个半无穷大圆围道会带来π的辐角变化，C1、C2则取决于 $j\infty$ 处的辐角，而 $j\infty$ 处，由于是无穷远的点，自然其辐角取决于 $a_n{a}_{n-1}$ 是否同号。这一系列转换，最终将问题转化为了Rouch表第一列是否同号的问题。

七、参考文献/书籍

1. 「何琴芳.证明Routh-Hurwitz稳定性判据的一个简明方法[J].电工教学,1992(03):12-18.」
2. 「俞菲,孟桥,樊祥宁.浅谈Routh-Hurwitz判据中的若干应用[J].电气电子教学学报,2013,35(01):12-14.」
3. 「曾禹村.信号与系统（第四版）[M].北京:北京理工大学出版社.2018,304-305」

---

1. 我们在习惯上认为：「虚轴上的一阶极点对应的临界稳定状态」也属于「不稳定状态」 ↩︎

2. 事实上，这样断言是不够严谨的，因为如果此时p(s)也是零点，实部虚部均为0，而复数0的辐角是没有意义的。但我们很容易舍去这种情况，因为根据1的讨论，$p_n$和$p_{n-1}$在虚轴上的零点是完全相同的，所以不会对辐角产生影响。 ↩︎