WB笔试复盘

选择题涉及数据结构、算法、逻辑分析、操作系统、数据库、java、linux、计算机网络，还蛮多的

一、选择题

1. n个人围成一圆圈，从第一个人开始一次报数，每轮到m的人被淘汰；如此循环，问最后剩下的一个人 是谁。这种问题最适合用那种数据类型描述（循环链表）
2. 假定58租房发布一个任务，其中发布操作可以分为5个子任务，每个子任务分别需要时间1s,2s,3s,4s,5s,若按照流水线方式执行，从头到尾完成25个发布任务所需时间为（125s）
3. 一颗完全二叉树有367个节点，则这颗二叉树的叶子节点有（184）个
   【二叉树性质】
   （1）n = n0+n1+n2;
   （2）n0 = n2+1;
   （3）由以上两式可得：n = 2n0+n1-1
   由于完全二叉树中度为1的节点（即叶子节点）数只有两种可能0或1，所以有n0 = n/2或n0 = （n+1）/2。
   满二叉树（满满当当的二叉树）： 定义一个二叉树，如果每一层的节点数都到达最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为k，且节点总数是（2^k）-1，则它就是满二叉树。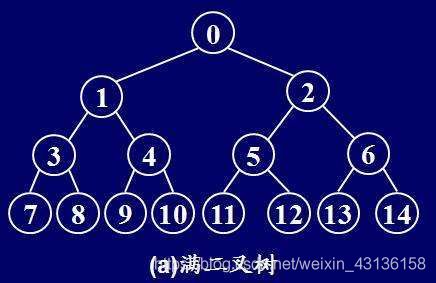
   完全二叉树： 二叉树深度为h，除了第h层外，其他各层（1~h-1）层的节点数都达到最大个数，第h层所有节点都连续集中在最左边，这就是完全二叉树。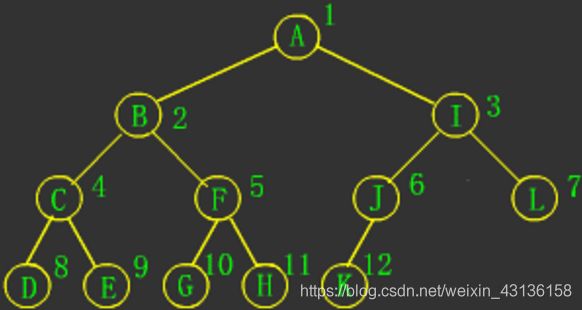
4. 下面是两颗完全二叉树的节点数，请问哪两棵树的深度相等（根的深度为1）：（65 120）
   A 65 120
   B 30 37
   C 62 77
   D 120 150
   【完全二叉树深度求法】h = log2(n)（向下取整）+1，完全二叉树第i层的节点个数为2^(i-1)，由图可得65和120在64~128之间，因此深度都为8.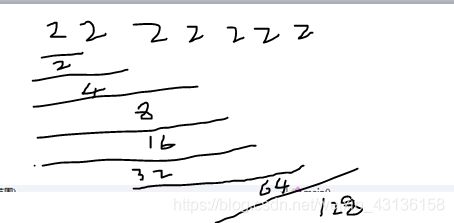
5. Dos攻击（DenialOfService，拒绝服务供给）中，攻击者与目标主机建立大量的TCP半链接，导致主机的资源耗尽的攻击方式是（SYN泛洪）
   【syn泛洪】SYN洪水攻击属于DoS攻击的一种，它利用TCP协议缺陷，通过发送大量的半连接请求，耗费CPU和内存资源。SYN攻击除了能影响主机外，还可以危害路由器、防火墙等网络系统，事实上SYN攻击并不管目标是什么系统，只要这些系统打开TCP服务就可以实施。【几种DOS攻击的介绍】
6. 如果一个栈的入栈顺序为ABCDEF，那么不可能的出栈顺序为：（A）
   A DBACFE
   B CDBEAF
   C ABFEDC
   D CBDEFA
   【栈的性质】先进后出，后进先出。像这种题就用性质去推理答案是否正确。
   A）项中，D在头，因此先是ABCD依次入栈，然后D出栈，接下来的出栈顺序只能是C或者D后边的E，因此A错；
   B）项中，C在头因此是ABC依次入栈，然后C出栈，接着D入栈，D再出栈，接着B出栈，接着E入栈E出栈，接着A出栈，最后F入栈F再出栈；
   C）项中，A入栈出栈，B入栈出栈，然后CDEF依次入栈再依次出栈；
   D）项中，ABC依次入栈，CB出栈，D入栈D出栈，E入栈E出栈，F入栈F出栈，最后A出栈
7. 以下选项均为性能测试子类型的是（负载测试、容量测试、压力测试、浸泡测试）
   【性能测试都有啥】性能测试：指通过自动化的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试。
   性能测试分为：基准测试、负载测试、压力测试、并发测试、容量测试、稳定性测试
   【浸泡测试是啥】浸泡测试(Soak Test)：Soak test是在一个稳定的并发用户上进行的long run测试，用来测试SOA应用程序的健壮性。通过soak test往往可以发现内存泄露，频繁 GC 等严重性能问题。进行soak test需要注意以下两点：

• Soak test需要在一定适中的用户负载量下进行，最好低于应用支持最大的负载量。
• 在执行long run测试时，采用几种不同用户组，并且每个用户组织性不同的业务流程。
  Soak test实际上比较简单的性能测试，测试最好能够运行几天，以真正得到一个健壮的应用。确保应用测试是贴近真实世界，尽量与实际使用情况接近。
  ——来自：基于SOA（面向服务的架构哦）的性能测试方法

8. 以下代码运行最终会导致结果为（死循环），while没有终止条件

public calaa sloution
{
public static void main(String[] args)
{
List list = new ArrayList();
while(true)
{
list.add(new Iteger (new Random().nextInt()));
}
}
}

9. 抽屉里500幅画按顺序编号为1、2、3…、499、500堆叠在一起。第一次把所有奇位号的画拿走，第二次再从剩下画中拿走奇数号的画，以此类推。请问最后剩下的一张画的编号是（256）
   500/250/128/256
   【分析】奇位号：数的位置为奇数
   奇数号：数的值为奇数
   然后以此类推这四个字说明，这两个步骤在不断的重复，直到最后剩下一张画结束。

10. 在操作系统中，关于文件索引结构描述正确的是（系统为每个文件都创建了一个专用的索引表）
    【操作系统：文件索引结构】索引结构指一个文件的信息存放在若干不连续的物理块中，系统为每个文件建立一个专用的数据结构——索引表，并将这些块的块号存放在索引表中。优点是保留了链表结构的优点，同时解决了其缺点，既能顺序存取，又能随机存取，满足了文件动态增长，插入删除的需求，也能充分利用外村空间。缺点是索引表本身带来一定的系统开销。

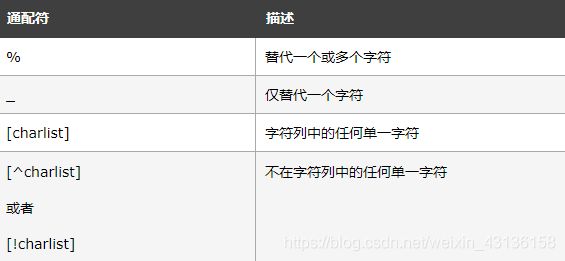
11. 经纪人信息表broker(id, name, company, city)其中有一个组合索引（name, company），下面哪个查询语句的索引是有效的？
    SELECT * FROM broker WHERE name like ‘%明’ ?
    【sql通配符】在搜索数据库中的数据时，sql通配符可以替代一个或多个字符。sql通配符必须与LIKE运算符一起使用。在sql中，可以使用以下通配符。
    

12. 在linux系统中，用户A有一个名为Test.sh的文件，如果想设置用户A的权限是读、写、执行；与用户A同属一个group的其他用户的权限是读、执行；其它group用户的权限是写、执行；那么下面哪个命令可以实现（chmod 753 Test.sh）
    【题意理解】Linux中设置用户权限读写执行，同组用户读执行，其他用户写执行的命令是啥
    【linux中设置目录权限】linux中使用chmod命令对目录设置权限；
    chmod可以用三个数字来表达用户，用户组，其他用户，比如：chmod 777 /test（三个7分别代表用户，用户组，其他用户，而数字7是特定用户的读，写，执行权限）
    读取——4
    写——2
    执行——1
    所以本题的命令就是chmod 753 Test.sh

13. 总监有3个下属，工龄和是13年，工龄的乘积等于总监的年龄，新招聘的助理知道总监的年龄，但是不能确认他3个直属下属工龄有多大。总监告诉他：“下属员工中只有1位工龄超过5年”，于是助理说“哦，我知道了”。所以总监的三个直属下属工龄都是多少（BorD？A工龄不能48年吧？C错）
    A 8 3 2
    B 8 4 1
    C 7 5 1
    D 9 2 2

14. 假设公司有两层（1层和2层），堆放电脑的数量比是3:1，若从1层将240台电脑运到2层上，则1层和2层的电脑数量比是3:5，求1层原来的电脑有多少台（480）
    【这tm就是个智力题】(3x-240)/(x+240) = 3:5，x=160，3x=480

15. 将二叉树通过单旋/双旋方式得到平衡二叉树进行中序遍历，得到的结果是：（5-10-15-17-20-25）
    
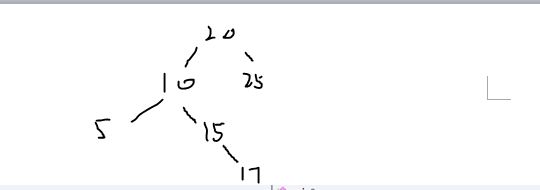
    【平衡二叉树的定义】平衡二叉树也叫平衡二叉搜索树，又被称为AVL树，可以保证查询效率较高。
    具有以下特点：它是一颗空树或它的左右两个子树的高度差的绝对值不超过1，并且 左右两个子树都是一颗平衡二叉树。
    首先要明确的是，平衡二叉树是一棵二叉排序树，它的出现是为了解决普通二叉排序树（普通二叉排序树）不平衡的问题。
    【平衡二叉树的单旋、双旋】
    【中序遍历】左根右

16. Linux系统，结构日志文件是/user/detail.log，日志打印了接口请求参数。小明在测试项目时，需要查看请求日志，以下哪条命令的查询结果能显示最近的10条请求（tail -n 10 /user/detail.log）

17. 现针对电商系统的订单提交功能进行性能测试，以下论述正确的是（响应时间和交易执行吞吐量都是用来衡量系统执行快慢的）

18. 如下网格，从A点出发只能向上向左走，走到B点，共有多少种走法（35）
    
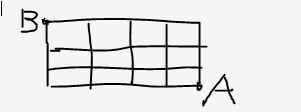
    【分析】我觉得是一个递归，每走一步就看该从A点到该点共有多少种走法（只能走左或上）
    例子，这是一个只能向右向下的例子，与本题意思其实相同，还给出了相应的代码，很清晰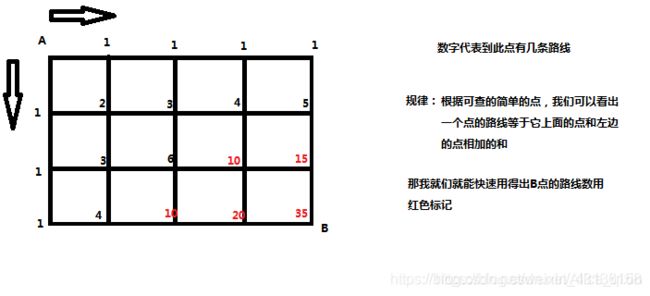

19. 下面哪个字段不会出现在http协议的请求头域里~~（Server）~~
    【http协议的请求头域里的字段有：】

• User-Agent：浏览器类型
• Connection：表示是否需要持久连接。
• Referer：包含一个URL，用户从该URL代表的页面出发访问当前请求的页面。

20. mysql如果想把时间字段sydate（timestamp）显示为“20200622 22:47”这样的格式，用什么语句（SELECT FROM_UNIXTIME(SYDATE, '%Y-%m-%d %H:%i') FROM dual）
    【分析：mysql将时间转换为时间戳】注意Y和H要大写，语法是FROM_UNIXTIME

21. 有如下IP地址172.16.13.5，其对应的子网掩码为255.255.255.128，那么该地址属于哪类地址？对应的网络地址及广播地址为（B类地址，网络地址172.16.13.0，广播地址172.16.13.255）
    【通过IP地址和子网掩码，如何计算出网络地址、广播地址和主机数？】

• 将IP地址和子网掩码换算为二进制，虚线前是网络地址，虚线后是主机地址
  
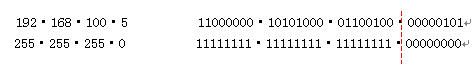
• 网络地址 = IP地址&子网掩码
• 广播地址：将上面的网络地址中的网络地址（前3段）部分不变，主机地址部分变为全1，结果就是广播地址。
  【本题解析】
  IP地址172.16.13.5换算为二进制为：10101100.00010000.00001101.00000101
  子网掩码255.255.255.128换算为二进制为：11111111.11111111.11111111.10000000
  则网络地址为这两个IP地址与子网掩码相与：10101100.00010000.00001101.00000000=172.16.13.0
  广播地址为10101100.00010000.00001101.11111111=172.16.13.255

22. 若某整数的补码为11110001，则该数的十进制数和二进制数分别为：（-15,10001111）
    【考点：原码、反码、补码】
    对于一个数，计算机要使用一定的编码方式进行存储，原码、反码、补码是机器存储一个具体数字的编码方式。

• 原码： 原码就是符号位加上真值的绝对值，**就是第一位表示符号（0正1负），其余值表示值。**比如8位二进制 [+1]原=0000 0001，因此8位二进制数的取值范围就是：[1111 1111 , 0111 1111]=[-127,127]
• 反码： 正数的反码是其本身，负数的反码是在其原码的基础上，符号位不变，其余各个位取反
  可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算。
  [+1] = [00000001]原 = [00000001]反
  [-1] = [10000001]原 = [11111110]反
• 补码： 正数的补码就是其本身，负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1（即反码+1）
• 总结
  符号位：0正1负
  正数：原码=反码=补码
  复数：反码=原码除符号位之外取反，补码=反码+1
• 为啥要设计原码、反码、补码？
  答：为了让计算机运算的设计更加简单；让符号位也参与运算，将减法变成了加法；简化计算机的设计

二、编程题

1 输出数组中所有满足的数字，以及它最小的“待加值”，每一行输出一个数组中的数字，空格，加上一个最小的“待加值”

• 题目描述： 给定一个没有重复元素的正整数数组m和一个正整数top。如：正整数数组m为[1,2,3,5,9,14]，top=9。
  对于数组来说最大的一个数字记为Max，则在给定的数组中，Max=14。
  我们希望在数组m中找到满足条件的一些数字，每个数字可以通过加上一个不大于top的正整数，得到大于Max的和。
  希望程序输出数组中所有满足的数字，以及它最小的“待加值”，每一行输出一个数组中的数字，空格，加上一个最小的“待加值”。
  输入示例
  9
  6
  1 2 3 5 9 14
  输出示例：
  9 6
  14 1
• 分析：读懂题意然后暴力解决即可
• 代码：

/*每一行输出一个数组中的数字，空格，加上一个最小的“待加值”*/
#include
#include
using namespace std;

int main()
{
     
	int top;
	int n;
	cin>>top>>n;
	vector<int> m(n);
	int max=0;
	for(int i=0;i<n;i++)
	{
     
		cin>>m[i];
		if(m[i]>max)
			max = m[i];	
	}
	for(int i=0;i<n;i++)
	{
     
		for(int j=1;j<=top;j++)
		{
     
			if(m[i]+j > max)
			{
     	cout<<m[i]<<" "<<j<<endl;
				break;
			}
		}
	}

	return 0;
}

2 找出1000-100000之间既是回文又是质数的数字

• 分析：
  写两个子函数：判断是否为回文，判断是否为质数
  然后遍历1000~100000，用if对每个数进行判断，若满足条件则输出。
  （1）判断质数（就是素数）：指的是在大于1的自然数中，除了1和它本身外，不能被其他自然数整除（除0外）的数。
  注意：判断一个数是x否为质数，并不需要将小于x的每个数都整除一次，只要将小于根号x的除一次就行了，因为若有大于根号x的i值，那x/i就必定是小于根号x的，在之前已经做过判定了。比如对于x=10=2*5，只需要让i等于2即可，判断效果是一样的。
  （2）判断回文数字：新定义一个sum去储存将原数字颠倒之后的数。
  比如对于123，在每次%10之后就得到最后一位的值，然后放入sum里，在/10将最后一位去除。

while(y)
{
     
	sum = sum*10 + y%10;
	y/=10;
}

• 代码：

#include
#include
using namespace std;

int isSushu(int x)
{
     
	int i;
	for(i=2;i*i<x;i++)//i*i
	{
     
		if(x%i==0)
			return 0;
	}
	return 1;
}

bool isHuiwen(int x)
{
     	
	int y=x, sum=0;
	while(y)
	{
     
		sum = sum*10 + y%10;
		y/=10;
	}
	if(sum == x)
		return true;
	else
		return false;
}

int main()
{
     
	for(int i=1000;i<=100000;i++)
	{
     
		if(isHuiwen(i) && isSushu(i))
		{
     
			cout<<i<<endl;
		}
	}

	return 0;
}

3 m支剑射中环数总和为n的方法

• 题目描述：
  给m支剑，每次射中的环数是0-10环（环数为正数，脱靶为0环），设置一个总环数为n，每支剑命中环数总和为n则获胜。为了获得比赛，共有多少种设计方法？
  输入描述：
  m为发放剑的数量，n为总环数
  输出描述：
  输出为射击方法的数量
  输入示例：
  8 40
  输出示例：
  9377467

• 分析：本题的题意就是从数组中选出m个数，使得这m个数的和为固定值n。本题的数组其实就是[0~10]这11个数。
  利用枚举法：对于本题的中数组其实就是[0,1,2,3,4,5,…,10]这么11个数，然后要从这11个数中找出m个数，使得和为固定值n。可以将这么11个数看成一个11位的二进制数即0 00000 00000~1 11111 11111，0代表该位置没选中，1就代表选中了，因此遍历二进制数进行枚举，找到二进制数中1的个数为m且加和的值为n的情况。

意思就是从数组（这11个数）里边选出m个数使得和为n，就是穷举所有这个12位中有6位的情况。按上述方法解得结果为13，并且每一例中数组的内容为图所示：

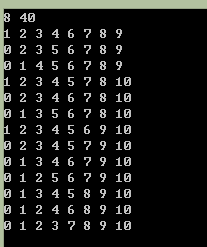
但本题没这么简单，本题要找出所有情况，包括一种情况下的不同排序，因此比上述解法复杂一些。
本题需要找出所有的情况并进行全排列，最终输出的是全排列的次数。

• 代码：只实现了部分功能

/*m个0-10的数相加总和为n的排列组合：小于等于10的m个数相加之和为n的排列组合*/
#include
#include
#include
#include
using namespace std;
int re = 0;

//leecode（剑指offer57）：数组中选出两个数相加使得和为固定数sum
vector<int> twoSum(vector<int>& nums, int target) 
{
     
    vector<int> result(2);
    map<int, int> maps;
    int len = nums.size();
    for(int i=0;i<len;i++)
    {
     
        maps[nums[i]] = i;//key为数组值，因之后要用到find函数来查询
    }
    map<int, int>::iterator iter;
    for(int i=0;i<len;i++)
    {
     
        iter = maps.find(target-nums[i]);//需要用迭代器来存储maps里的值
        if(nums[i]<=target && iter!=maps.end())
        {
     
            result[0] = nums[i];
            result[1] = target - nums[i];
            break;//找到一对就行了
        }
    }

    return result;
}

//本题：数组中选出m个数相加使得和为固定值n，求排列组合的方法数【现只实现了符合和为n的排列】
int NumOf1(int num)//统计值num的二进制中1的个数
{
     
	int count = 0;
	while(num)
	{
     
		num = num&(num-1);//num每与num-1与一次，就将二进制最右边的1变成0
		count++;
	}
	return count;
}

int CountSumIsN(vector<int> &nums, int target, int m)
{
     
	int len = nums.size();
	int bit = 1<<(len);//从1循环到i=2^(len)
	for(int i=1;i<bit;i++)
	{
     
		int sum = 0;
		vector<int> tmp;
		if(NumOf1(i) == m)//将二进制中1的个数进行统计，为m则累加求和看是不是目标值n
		{
     
			for(int j=0;j<len;j++)
			{
     
				if((i & (1<<j)) != 0)//1与2^j进行与运算，若结果不为0，则i位置处就有值
				{
     
					sum += nums[j];
					tmp.push_back(nums[j]); 
				}
			}
			if(sum == target)
			{
     
				re = re+1;
			}
		}
	}
	return re;

}   
int main()
{
     /*
	
	vector x(4);
	for(int i=0;i<4;i++)
	{
		cin>>x[i];
	}
	
	vector r = twoSum(x, 9);
	for(int i=0;i<2;i++)
	{
		cout<

	int m,n;
	cin>>m>>n;
	vector<int> x(11);
	for(int i=0;i<=10;i++)
	{
     
		x[i] = i;
	}
	int r = CountSumIsN(x, n, m); 
	cout<<r<<endl;

	return 0;
}