设计32信道的多相滤波结构数字接收机
设计32信道的多相滤波结构数字接收机
- 一 、实验题目
- 二、 实验原理
- 三、MATLB仿真过程与结果分析
-
- MATLAB代码
一 、实验题目
单通道实采样,采样率2.4GHz。设计32信道的多相滤波结构数字接收机,给出各信道的通带范围,采用MATLAB工具设计原型滤波器,给出原型滤波器特性。结合相位差分测频算法,输入不同频率的信号,测试数字接收机各信道输出,并完成信号频率测量。
二、 实验原理
32信道多相滤波器结构图如下:
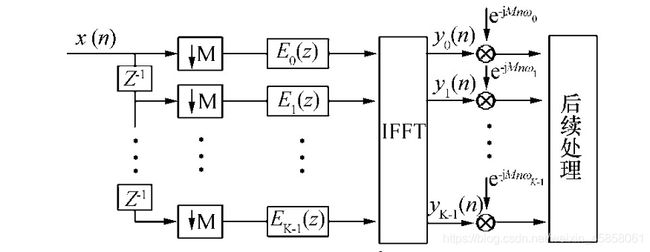
多相滤波器结构是实现信道化接收机的高效结构, 它是把带通滤波器变成多相一致离散傅里叶变换的滤波器组, 可以通过对原型滤波器系数进行抽取来实现。多相信道化接收机是在直接信道化接收机的基础上改进得来。直接信道化接收机通过利用不同频率响应的带通滤波器组将信号划分到不同的信道上得到信号回波信息。当有K个信道, 且滤波器组为理想的, 则每个滤波器的带宽为fs/K。但理想滤波器组不可能实现, 通常会存在过渡带, 若过渡带之间没有重叠, 滤波器组如图2所示。这样就产生了信道间的盲区, 当信号落入盲区时则无法检测。
信道化的无盲区实现决定了每个信道的通带带宽设定为fs/K, 当信道数目K值确定后, 滤波器的过渡带宽就决定了信道的带宽, 由于信道间会有交叠, 某个信号应该尽量在一个信道或者其附近某一个信道内出现, 某个信号应该尽量在一个信道或者其附近某一个信道内出现, 所以过渡带的范围为0
设定采样率fs为1.8 GHz, 信道化数目为32, 通带波动为0.1 dB, 阻带衰减损耗设为60 dB, 仿真过渡带宽对滤波器阶数的影响如图4所示, 从图4中, 可以得出过渡带宽越窄则原型滤波器所需要的阶数就越大。过渡带宽对瞬态响应时间的影响如图5所示, 得出过渡带越窄, 滤波器瞬态响应时间T越长。从两幅图中可以看出, 过渡带宽越窄, 相应的变化越明显, 同时, 滤波器的阶数与其瞬态响应时间成线性正比。在滤波器瞬态响应期间, 其输出信号的幅度和频率都会发生改变, 输入脉冲经过滤波器时, 若稳定时间太短, 其频率就不能被正确的估计。所以在设计滤波器时, 要考虑系统需要处理的最小脉冲宽度。定义最小脉冲宽度为Tp, 需要满足Tp>T。
为精确得到输入信号频率需要对滤波结果作相位差分,频域中的相位差分法与时域中的相位差分法类似,都是利用频率与相位和时间的关系。设采样频率为fs 的复单频输入信号为:
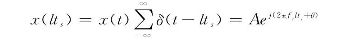
式中:l为整数,ts为采样时间,A为信号的幅度,fr为实际频率,θ为初始相角。对其做N点FFT变换有
![]()
通过上式可知,将x在频域上展开后,可以通过最大峰值M(0
式中:Δt表示时延,argXΔt(M)表示经过Δt时延后做N点FFT变换后M点的相角值,而argX0(M)则表示初始时刻的N点FFT变换后M点的相角值。从上式中可以看出,当经过的时延Δt越大,则得到的频率值fs越精确。但是随着Δt的增大,另一个问题也出现了,就是argXΔt(M)会随着Δt的增加而不断地成周期性的变化。
三、MATLB仿真过程与结果分析
通过上面分析,编写MATLAB程序设计32信道多相滤波器
其通带范围如下:
| 信道数 | 通带范围/MHZ | 信道数 | 通带范围/MHZ | 信道数 | 通带范围/MHZ | 信道数 | 通带范围/MHZ |
|---|---|---|---|---|---|---|---|
| 信道1 | (-1200,-1100) | 信道9 | (-600 , -525) | 信道17 | (75 , 150) | 信道25 | (675 , 750) |
| 信道2 | (-1100,-1025) | 信道10 | (-525 , -450) | 信道18 | (150 , 225) | 信道26 | (750 , 825) |
| 信道3 | (-1025, -975) | 信道11 | (-450 , -375) | 信道19 | (225 , 300) | 信道27 | (825 , 900) |
| 信道4 | (-975 , -900) | 信道12 | (-375 , -300) | 信道20 | (300 , 375) | 信道28 | (900 , 975) |
| 信道5 | (-900 , -825) | 信道13 | (-300 , -225) | 信道21 | (375 , 450) | 信道29 | (975 ,1025) |
| 信道6 | (-825 , -750) | 信道14 | (-225 , -150) | 信道22 | (450 , 525) | 信道30 | (1025,1100) |
| 信道7 | (-750 , -675) | 信道15 | (-150 , -75) | 信道23 | (525 , 600) | 信道31 | (1100,1175) |
| 信道8 | (-675 , -600) | 信道16 | (-75 , 75) | 信道24 | (600 , 675) | 信道32 | (1175,1200) |
信号为实采样,采样率2.4GHZ,产生一频率为100HZ的正弦信号如下图:

对其做傅里叶变换得到频谱如下图:

由图可知信号在±100HZ处有两频谱分量,将其通过32信道多相滤波器,第11到第23信道输出如下图:

由仿真结果可知此信号只在第16信道有输出,第16信道通带为-75MHZ–75MHZ,
信号频率为100HZ,符合预期情况。
编写程序对上面结果作相位差分得到结果为:

与真实值基本一致。
MATLAB代码
clear all;close all;clc;
figure;
FS=2.4e+9;
IF=35e+7;
MF=3.6e+9;
Signal_DDC=0:1:1000;
Signal_DDC=Signal_DDC/1000;
Signal_DDC=sin(2*pi*100*Signal_DDC);
N=length(Signal_DDC);
nfft=2^nextpow2(N);
t_axis=(0:N-1)./fs;
f_axis=(0:nfft-1)./nfft*fs-fs/2;
subplot(211)
plot(t_axis.*1e6,real(Signal_DDC));
xlabel('时间')
title('输入信号')
subplot(212)
Signal_DDC_fft=(fftshift(fft(Signal_DDC,nfft)));
plot(f_axis./1e6,(abs(Signal_DDC_fft)))
xlabel('频率')
title('输入信号的频谱')
fI=IF;
K=32;
Channel_Freq_Range=[((0:K-1)-(K-1)/2).*fs/K-fs/K/2;((0:K-1)-(K-1)/2).*fs/K+fs/K/2]./1e6;
h_LP=fir1(1023,1/K,'low');
M=length(h_LP);
Q=fix(M/K);
H=zeros(K,Q);
for d=1:K
H(d,:)=h_LP(d:K:(Q-1)*K+d);
end
tic;
temp=mod(length(Signal_DDC),K);
if temp~=0
Signal_DDC0=[Signal_DDC(1:end),zeros(1,K-temp)];
X=reshape(Signal_DDC0,K,length(Signal_DDC0)/K);
else
X=reshape(Signal_DDC(1:end),K,length(Signal_DDC)/K);
end
X=flipud(X);
[rx,L]=size(X);
if mod(K,2)==0
X=X.*repmat((-1).^(0:L-1),K,1);
end
Y=zeros(K,L);
for d=1:K
Y(d,:)=Filter_FFT(X(d,:),H(d,:));
end
for ll=1:L
temp=Y(:,ll).*(-1).^(0:K-1).';
temp=temp.*exp(j*(0:K-1).'*pi/K);
Y(:,ll)=ifft(temp,K).*K;
end
toc;
figure;
range=14:27;
for d=1:length(range)
if mod(length(range),2)==0
subplot(length(range)/2,2,d);
else
subplot((length(range)+1)/2,2,d);
end
t_axis=((0:L-1))./fs.*K+(range(d)-1)./fs;
plot(t_axis.*1e6,abs(Y(range(d),:)))
ylim([0 max(max(abs(Y)))+1])
End
for m=1:460
f = 150+m*5;
sig = floor(127*sin(2*pi*f*t));
sig_vec = reshape(sig,32,N/32)';
y = fft(sig_vec,[],2);
y = y(:,1:16);
[max_value,max_idx] = max(abs(y(1,:)));
phase_ori = angle(y(:,max_idx))';
sub_pse_ori = phase_ori(1,2:end) - phase_ori(1,1:end-1);
for n = 1:length(sub_pse_ori)
if(sub_pse_ori(1,n)>=pi)
sub_pse_hand(1,n) = sub_pse_ori(1,n)-2*pi;
elseif(sub_pse_ori(1,n)<=-pi)
sub_pse_hand(1,n) = sub_pse_ori(1,n)+2*pi;
else
sub_pse_hand(1,n) = sub_pse_ori(1,n);
end
end
pse_unwrap = unwrap(phase_ori);
sub_pse_unwrap = pse_unwrap(1,2:end) - pse_unwrap(1,1:end-1);
diff = sub_pse_hand-sub_pse_unwrap;
sub_pse_0 = sub_pse_hand;
ratio_0 = sum(sub_pse_0(1,1:8))/8/2/pi;
sub_pse_1 = sub_pse_unwrap;
ratio_1 = sum(sub_pse_1(1,1:8))/8/2/pi;
a_result(1,m) = max_idx-1+ratio_0;
b_result(1,m) = max_idx-1+ratio_1;
c_result(1,m) = f/FS*32;
end