Python描述数据结构之最小生成树篇

前言

  本篇章主要介绍图的最小生成树，包括Prim算法和Kruskal算法，并用Python代码实现。

1. 创建图

  在开始之前，我们先创建一个图，使用邻接矩阵表示图：

class Graph(object):
    """
    以邻接矩阵为存储结构创建无向网
    """
    def __init__(self, kind):
        # 图的类型: 无向图, 有向图, 无向网, 有向网
        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,
        self.kind = kind
        # 顶点表
        self.vertexs = []
        # 边表, 即邻接矩阵, 是个二维的
        self.arcs = []
        # 当前顶点数
        self.vexnum = 0
        # 当前边(弧)数
        self.arcnum = 0

    def CreateGraph(self, vertex_list, edge_list):
        """
        创建图
        :param vertex_list: 顶点列表
        :param edge_list: 边列表
        :return:
        """
        self.vexnum = len(vertex_list)
        self.arcnum = len(edge_list)
        for vertex in vertex_list:
            vertex = Vertex(vertex)
            # 顶点列表
            self.vertexs.append(vertex)
            # 邻接矩阵, 初始化为无穷
            self.arcs.append([float('inf')] * self.vexnum)
        for edge in edge_list:
            ivertex = self.LocateVertex(edge[0])
            jvertex = self.LocateVertex(edge[1])
            weight = edge[2]
            self.InsertArc(ivertex, jvertex, weight)

    def LocateVertex(self, vertex):
        """
        定位顶点在邻接表中的位置
        :param vertex:
        :return:
        """
        index = 0
        while index < self.vexnum:
            if self.vertexs[index].data == vertex:
                return index
            else:
                index += 1

    def InsertArc(self, ivertex, jvertex, weight):
        """
        创建邻接矩阵
        :param ivertex:
        :param jvertex:
        :param weight:
        :return:
        """
        if self.kind == 'Undinetwork':
            self.arcs[ivertex][jvertex] = weight
            self.arcs[jvertex][ivertex] = weight

  有关邻接矩阵中顶点结点Vertex()的定义可以参考这篇博客，这里就不在贴出相应的代码了。

2. 问题来源

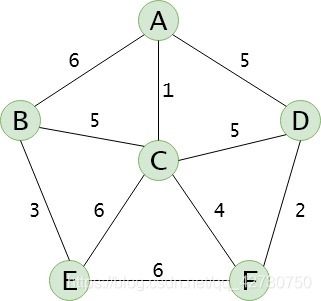
  假设要在$n$个城市之间建立通信联络网，则连通$n$个城市只需要$n-1$条线路。在每两个城市之间都可以建立一条线路，相应地都要付出一定的经济代价，$n$个城市之间最多可以建立$\frac{n(n-1)}{2}$条线路。这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个连通网，即如何在这些可能的线路中选择$n-1$条，以使花费的经费最少。
  我们可以用连通网来表示$n$个城市以及$n$个城市间可能建立的通信线路，其中顶点可以表示城市，边可以表示两个城市之间的通信线路，边的权值就是修建这条线路所需的经费。对于$n$个顶点的连通网可以建立许多不同的生成树，每一棵树都可以是一个连通网，现在要从中选择出一棵使用经费最少的生成树。这个问题就是构造连通网的最小代价生成树$(Minimum$ $Cost$ $Spanning$ $Tree)$的问题，简称最小生成树$(MST)$问题。
  MST的性质：假设$N=(V,\{E\})$是一个连通网，$U$是顶点集$V$的一个非空子集。若$(u,v)$是一条具有最小权值的边，其中$u\in U,v\in V-U$，则必存在一棵包含边$(u,v)$的最小生成树。
  $Prim$算法和$Kruskal$算法是两个利用MST性质构造最小生成树的经典算法。

3. Prim算法

  $Prim$算法，中文名叫普里姆算法。基本思想如下：
  (1) 指定连通网$N$中的某一顶点作为构造最小生成树的起点，并令$U=\{w\},TE=\{\}$；
  (2) 在所有$u\in U、v\in V-U$的边中，找到一条权值最小的边$(u,v)\in E$，将$u$并入到$U$中，并将边$(u,v)$并入到$TE$中；
  (3) 重复执行第二步，直到$U=V$，此时最小生成树包含$n-1$条边。
  这里使用一个辅助数组closedge，用来存储从$U$到$U-V$中权值最小的边及顶点$U$的下标，除此之外还需要一个列表arc来存储最小生成树的边。下面结合着$Prim$算法来分析一下上面的那个无向网：

  (1) $Prim$算法一直在更新两个集合，即已访问顶点集合$U$和未访问顶点集合$U-V$，然后从这两个集合组成的边中选择权值最小的边。这里以顶点$A$为起始点，先将它加入$U$中，即其对应的closedge置为$[(0,0)]$。此时$U$中只有顶点$A$，与$A$相连的边有$AB$、$AC$和$AD$，初始closedge为$[(0,0),(0,6),(0,1),(0,5),(0,\infty ),(0,\infty )]$，其中权值最小的边的另一个顶点索引为2，即顶点$C$，然后根据这个索引2确定了该边对应两个顶点的索引$(0,2)$，即边$AC$，图中的红色线表示，将该边加入到列表arc中，同时将$C$加入$U$中，即将其对应的closedge由$(0,1)$置为$(0,0)$，此时closedge为$[(0,0),(0,6),(0,0),(0,5),(0,\infty ),(0,\infty )]$；
  (2) 此时$U$中有顶点$A$和$C$，然后去找两顶点集合对应权值最小的边，与$C$相连的边有$CA$、$CB$、$CD$、$CE$和$CF$，更新closedge为$[(0,0),(2,5),(0,0),(0,5),(2,6),(2,4)]$，更新的原则是如果新边的权重比closedge中的小，更新，否则不更新，其中权值最小的边的另一个顶点索引为5，即顶点$F$，然后根据这个索引5确定了该边对应两个顶点的索引$(2,5)$，即边$CF$，图中的橙色线表示，将该边加入到列表arc中，同时将$F$加入$U$中，即将其对应的closedge由$(2,4)$置为$(2,0)$，此时closedge为$[(0,0),(2,5),(0,0),(0,5),(2,6),(2,0)]$；
  (3) 此时$U$中有顶点$A$、$C$和$F$，然后去找两顶点集合对应权值最小的边，与$F$相连的边有$FC$、$FD$和$FE$，更新closedge为$[(0,0),(2,5),(0,0),(5,2),(2,6),(2,0)]$，其中权值最小的边的另一个顶点索引为3，即顶点$D$，然后根据这个索引3确定了该边对应两个顶点的索引$(5,2)$，即边$FD$，图中的黄色线表示，将该边加入到列表arc中，同时将$D$加入$U$中，即将其对应的closedge由$(5,2)$置为$(5,0)$，此时closedge为$[(0,0),(2,5),(0,0),(5,0),(2,6),(2,0)]$；
  (4) 此时$U$中有顶点$A$、$C$、$F$和$D$，然后去找两顶点集合对应权值最小的边，与$D$相连的边有$DA$、$DC$和$DF$，更新closedge为$[(0,0),(2,5),(0,0),(5,0),(2,6),(2,0)]$，其中权值最小的边的另一个顶点索引为1，即顶点$B$，然后根据这个索引1确定了该边对应两个顶点的索引$(2,1)$，即边$CB$，图中的绿色线表示，将该边加入到列表arc中，同时将$B$加入$U$中，，即将其对应的closedge由$(2,5)$置为$(2,0)$，此时closedge为$[(0,0),(2,0),(0,0),(5,0),(2,6),(2,0)]$；
  (5) 此时$U$中有顶点$A$、$C$、$F$、$D$和$B$，然后去找两顶点集合对应权值最小的边，与$B$相连的边有$BA$、$BC$和$BE$，更新closedge为$[(0,0),(2,0),(0,0),(5,0),(1,3),(2,0)]$，其中权值最小的边的另一个顶点索引为4，即顶点$E$，然后根据这个索引4确定了该边对应两个顶点的索引$(1,4)$，即边$BE$，图中的蓝色线表示，将该边加入到列表arc中，同时将$E$加入$U$中，，即将其对应的closedge由$(2,6)$置为$(1,3)$，此时closedge为$[(0,0),(2,0),(0,0),(5,0),(1,0),(2,0)]$；
  至此，未访问顶点的集合已为空，顶点已全部被访问，最小生成树为：$\{(A,C),(C,F),(F,D),(C,B),(B,E)\}$。
  $Prim$算法实现如下：

    def GetMin(self, closedge):
        """
        找到当前closedge中权值最小的边
        :param closedge: 
        :return: 
        """
        index = 0
        vertex = 0
        minweight = float('inf')
        while index < self.vexnum:
            if closedge[index][1] != 0 and closedge[index][1] < minweight:
                minweight = closedge[index][1]
                vertex = index
            index += 1
        return vertex

    def Prim(self, start_vertex):
        k = self.LocateVertex(start_vertex)
        closedge = []
        arc = []
        for index in range(self.vexnum):
            # 下标权值, 初始化
            closedge.append([k, self.arcs[k][index]])
        # 将起始点加入到U中
        closedge[k][1] = 0
        index = 1
        while index < self.vexnum:
            # 找到了与下标为k相连的最小边
            minedge = self.GetMin(closedge)
            # 将当前最小权值的边加入到最小生成树arc
            arc.append([self.vertexs[closedge[minedge][0]].data, self.vertexs[minedge].data, closedge[minedge][1]])
            # 将最小边权值置为0, 即将顶点v加入U中, 表示该顶点已经在最小生成树内
            closedge[minedge][1] = 0
            i = 0
            # 重新选择权值最小边
            while i < self.vexnum:
                if self.arcs[minedge][i] < closedge[i][1]:
                    # 更新 最小边的权值及下标
                    closedge[i] = [minedge, self.arcs[minedge][i]]
                i += 1
            index += 1
        return arc

  可以看到$Prim$算法的时间复杂度与图中顶点的数目有个很大关系，所以它更适合稠密网求最小生成树。

4. Kruskal算法

  $Kruskal$算法，中文名叫克鲁斯卡尔算法。基本思想如下：
  (1) 将连通网$N$中的所有边存入集合Edges，并按权值从小到大进行排列，同时令$U=V,TE=\{\}$，$TE$是$N$上最小生成树中边的集合，此时为空，即最小生成树$T$中的每一个顶点都自带一个连通分量；
  (2) 依次访问Edges中的边，若当前被访问的边的两个顶点属于不同的连通分量，即不构成环，则将该边加入到$TE$中，并标记当前两个顶点所在的连通分量为同一个连通分量；否则将该边从Edges中删除；
  (3) 重复执行第二步，直到最小生成树$T$的所有顶点均属于同一连通分量，此时$Edges$中的边与组成最小生成树$T$的边相同，这些边组成了集合$TE$。

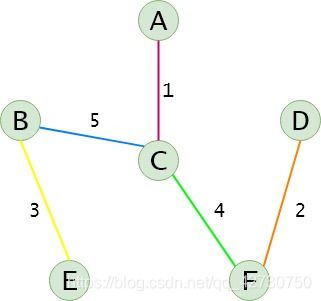
  这里使用一个辅助数组flags来记录每个顶点所属的连通分量的序号。下面结合着$Kruskal$算法来分析一下上面的那个无向网：
  (1) $Kruskal$算法在不断遍历列表edges中的每一条边并更新列表edges。首先遍历第一条边$(A,C)$，图中的红色线，发现这条边的两个顶点属于不同的连通分量，然后就更新辅助数组flags中对应顶点的序号，让它们俩的序号一致；
  (2) 然后遍历下一条边$(D,F)$，图中的橙色线，发现这条边的两个顶点属于不同的连通分量，然后就更新辅助数组flags中对应顶点的序号，让它们俩的序号一致；
  (3) 然后遍历下一条边$(B,E)$，图中的黄色线，发现这条边的两个顶点属于不同的连通分量，然后就更新辅助数组flags中对应顶点的序号，让它们俩的序号一致；
  (4) 然后遍历下一条边$(C,F)$，图中的绿色线，发现这条边的两个顶点属于不同的连通分量，然后就更新辅助数组flags中对应顶点的序号，让它们俩的序号一致；
  (5) 然后遍历下一条边$(A,D)$，发现这条边的两个顶点属于相同的连通分量，即加入这条边后，无向网就会产生回路，删除列表edges中的这条边；
  (6) 然后遍历下一条边$(B,C)$，图中的蓝色线，发现这条边的两个顶点属于不同的连通分量，然后就更新辅助数组flags中对应顶点的序号，让它们俩的序号一致；
  (7) 然后遍历下一条边$(C,D)$，发现这条边的两个顶点属于相同的连通分量，即加入这条边后，无向网就会产生回路，删除列表edges中的这条边；
  然后继续遍历，直至遍历完列表edges，列表edges中剩余的边就构成了最小生成树，最小生成树为：$\{(A,C),(D,F),(B,E),(C,F),(B,C)\}$。
  $Kruskal$算法实现如下：

    def AddEdges(self):
        """
        将连通网中的边加入到列表AddEdges中
        :return:
        """
        edges = []
        i = 0
        while i < self.vexnum:
            j = 0
            while j < self.vexnum:
                if self.arcs[i][j] != float('inf'):
                    edges.append([self.vertexs[i].data, self.vertexs[j].data, self.arcs[i][j]])
                j += 1
            i += 1
        # 按权重从小到大进行排序
        return sorted(edges, key=lambda item: item[2])

    def Kruskal(self):
        edges = self.AddEdges()
        flags = []
        for index in range(self.vexnum):
            flags.append(index)
        index = 0
        while index < len(edges):
            ivertex = self.LocateVertex(edges[index][0])
            jvertex = self.LocateVertex(edges[index][1])
            if flags[ivertex] != flags[jvertex]:
                # 两个顶点不属于同一连通分量
                # 找到它们各自的连通分量的序号
                iflag = flags[ivertex]
                jflag = flags[jvertex]
                # 它们两个如何合并, 找找flags有没有与之相同的
                limit = 0
                while limit < self.vexnum:
                    if flags[limit] == jflag:
                        # 将j和i的连通序号设置相同, 表示它俩是连通的
                        flags[limit] = iflag
                    limit += 1
                # index就要放这里, 因为删除边后edges长度就会减少1
                index += 1
            else:
                # 已经连通了, 即加入这条边就构成了环
                # 删除这条边
                edges.pop(index)
        return edges

  可以看到$Kruskal$算法的时间复杂度与图中边的数目有个很大关系，所以它更适合稀疏网求最小生成树。

5. 代码测试

  测试代码如下：

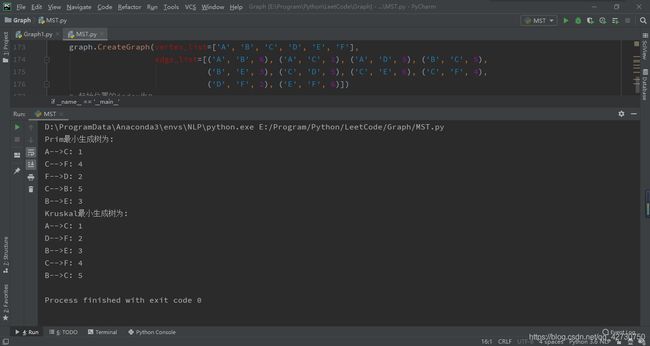
if __name__ == '__main__':
    graph = Graph(kind='Undinetwork')
    graph.CreateGraph(vertex_list=['A', 'B', 'C', 'D', 'E', 'F'],
                      edge_list=[('A', 'B', 6), ('A', 'C', 1), ('A', 'D', 5), ('B', 'C', 5),
                                 ('B', 'E', 3), ('C', 'D', 5), ('C', 'E', 6), ('C', 'F', 4),
                                 ('D', 'F', 2), ('E', 'F', 6)])
    # 起始位置的index为0
    mst1 = graph.Prim('A')
    print('Prim最小生成树为: ')
    for edge in mst1:
        print('{0}-->{1}: {2}'.format(edge[0], edge[1], edge[2]))
    mst2 = graph.Kruskal()
    print('Kruskal最小生成树为: ')
    for edge in mst2:
        print('{0}-->{1}: {2}'.format(edge[0], edge[1], edge[2]))

  测试结果如下：

  B站一位大佬制作的$Prim$算法和$Kruskal$算法动态演示。