第一次接触方向导数与梯度的概念,是在大学的高等数学课堂上,当时对于这部分内容是似懂非懂的。
巧合的是,后来在参加硕士复试的时候,有位老师提问我对方向导数与梯度的理解,当时我只记得一句话:梯度是方向导数变化最大的方向。虽然后来这位老师成了我的导师,但是现在想来依然觉得惭愧,因为我对这两个名词完全没有理解。
后来学习到BP神经网络,也手动推导过根据梯度下降法得到的权值更新公式,但方向导数的定义一直是我的心结。今天终于花了时间将这个简单的问题弄明白,特地记录下来,以警示自己在将来的科研道路上要脚踏实地,不可浮于表面!
1.方向导数
- 方向导数的本质是一个数值,简单来说其定义为:
一个函数沿指定方向的变化率。
因此,构建方向导数需要有两个元素:
1) 函数
2) 指定方向
当然,与普通函数的导数类似,方向导数也不是百分之百存在的,需要函数满足在某点处可微,才能计算出该函数在该点的方向导数。
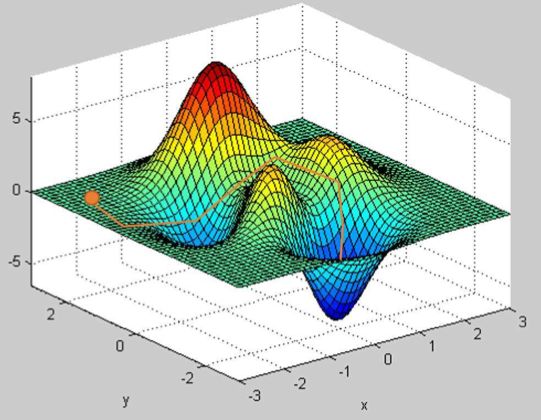
至于其物理含义,这里采用最常用的下山图来表示。
简单将上图看作是一座山的模型,我们处在山上的某一点处,需要走到山下。理论上来说,这座山的表面是可以通过一个函数的描述的(虽然想要找到这个函数可能很难),而这个函数可以在不同的方向上都确定出一个方向导数,这就好比于如果我们想下山,道路并不是唯一的,而是可以沿任何方向移动。区别在于有些方向可以让我们下山速度更快,有些方向让我们下山速度更慢,有些方向甚至引导我们往山顶走(也可以理解为下山速度时负的)。在这里,速度的值就是方向导数的直观理解。
2.梯度
- 梯度与方向导数是有本质区别的,梯度其实是一个向量,其定义为:
一个函数对于其自变量分别求偏导数,这些偏导数所组成的向量就是函数的梯度。
在很多资料中可以看到如下的梯度定义方法:
诚然,这种定义方法更加权威,但是却不够直观,这也是为什么我在高等数学课堂上学习梯度概念时感觉云里雾里。这种定义方法只针对二元函数,所以公式中的i,j可分别表示为函数在x和y方向上的单位向量,这样的描述可以让我们更好理解(因为人类大脑可以比较轻松的理解三维世界的模型图),但是一旦到了更高维度的世界,单纯靠这个公式就不容易理解了。
3.梯度与方向导数的关系
- 梯度与方向导数的关系应该如何描述呢?
函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
以上描述非常好理解,那如何证明呢?
说实话,我觉得以上证明过程很抽象,但这就是数学,而我们要做的就是从这些抽象中来理解问题的实质。
依然采用下山的例子来解释。我们想要走到山下,道路有千万条,但总有一条可以让我们以最快的速度下山。当然,这里的最快速度仅仅作用在当前的位置点上,也就是说在当前位置A我们选择一个方向往山下走,走了一步之后到达了另外一个位置B,然后我们在B位置计算梯度方向,并沿该方向到达位置处c,重复这个过程一直到终点。但是,如果我们把走的每一步连接起来构成下山的完整路线,这条路线可能并不是下山的最快最优路线。
原因是什么?可以用一句古诗来解释:“不识庐山真面目,只缘身在此山中。”因为我们在山上的时候是不知道山的具体形状的,因此无法找到一条全局最优路线。那我们只能关注脚下的路,将每一步走好,这就是梯度下降法的原理。