软件工程基础个人项目——数独终局生成和求解

GitHub项目地址

DropLee/Sudoku

项目任务描述

实现一个命令行程序，程序能：
1.生成不重复的数独终局至文件
2.读取文件内的数独问题，求解并将结果输出到文件

耗费时间估计

PSP2.1	Personal Software Process Stages	预估耗时（min）	实际耗时（min）
Planning	计划	120
Estimate	估计这个任务需要多少时间	2000
Development	开发	1800
Analysis	需求分析（包括学习新技术）	30
Design Spec	生成设计文档	30
Design Review	设计复审（和同事审核审计文档）	10
Coding Standard	代码规范（为目前的开发制定合适的规范）	20
Design	具体设计	180
Coding	具体编码	1200
Code Review	代码复审	120
Test	测试（自我测试，修改代码，提交修改）	120
Reporting	报告	240
Test Report	测试报告	30
Size Measurement	计算工作量	30
Postmortem & Process Improvement Plan	事后总结，并提出过程改进计划	120
	合计	2250

解题思路描述

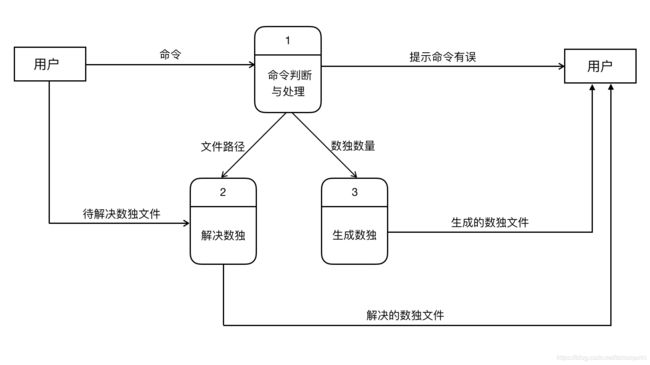
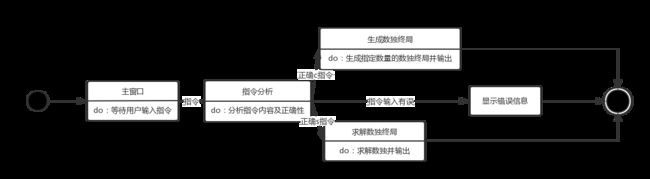
程序分为两个功能模块：生成数独终局、解决数独。两个功能模块互相独立，没有什么联系，通过不同的命令行参数调用，但需要有一定的错误判断和处理能力。

功能建模

顶层图：

1层图：

行为建模：

生成终局算法

题目要求要最多能生成 1000000 种不重复的终局，且第1行的第1个数字必须是个人学号最后两位之和对9的模再加1，则可以在1个现有的模板的基础上进行行内轮换和行间轮换。

行内轮换

第一个数字是固定的，故只能交换其他8个数字，第一行交换时，剩下的8行也会跟着进行位置的交换，这样使得数字间的位置关系不会破坏数独条件，此时生成 8！ 种终局

行间轮换

第一行第一个数字固定不变，故第一行将永远在第一行，而剩下的行之间可以进行轮换，如：2、3行之间交换，4、5、6行之间轮换，7、8、9行之间轮换，此时生成 2！*3！*3！ 种终局
如此，总共则生成

8！*2！*3！*3！=2903040（种）

满足要求

求解终局算法

参考 暴力算法之美：如何在1毫秒内解决数独问题？| 暴力枚举法+深度优先搜索 POJ 2982
基于暴力枚举和深度优先搜索，并将空白格按照可填数字数目从小到大进行排序，优先搜索可填数字少的空白格，减少大量递归调用自身的时间。

设计实现

主要函数

CreateSudoku() //生成数独终局的函数
关键代码

do
	{
     
		for (int i = 0; i < 9; ++i)        //make transform table
			trans[g_row[0][i] - 49] = arr[i];

		for (int i = 0; i < 9; ++i)        //transform 9 rows of sudoku and save in newRow
			for (int j = 0; j < 9; ++j)
				newRow[i][j] = trans[g_row[i][j] - 49];

		for (int i = 0; i < 2 && n; i++)    //Swap rows of transformed sudoku and save in temp array
		{
     
			for (int j = 0; j < 6 && n; j++)
			{
     
				for (int k = 0; k < 6 && n; k++)
				{
     
					for (int m = 0; m < 9; ++m)
					{
     
						for (int n = 0; n < 9; ++n)
						{
     
							g_output[tempPointer++] = newRow[order[m]][n] + '0';
							if (n == 8)
								g_output[tempPointer++] = '\n';
							else
								g_output[tempPointer++] = ' ';
						}
					}
					if (--n)
						g_output[tempPointer++] = '\n';
					else
						return;
					next_permutation(order + 6, order + 9);
				}
				next_permutation(order + 3, order + 6);
			}
			next_permutation(order + 1, order + 3);
		}
	} while (next_permutation(arr + 1, arr + 9));    //change the transform order
	return;
}

SolveSudoku() //解决数独问题的函数
关键代码

for (int r = 1; r < 10; r++)
		{
     
			for (int c = 1; c < 10; c++)
			{
     
				unsolvedSudoku[r][c] = g_input[iPointer++] - 48;

				if (unsolvedSudoku[r][c] == 0)   //count and save blanks
				{
     
					blank[blankCounter][0] = r;
					blank[blankCounter][1] = c;
					blankCounter++;
				}
				else                            //save the filled numbers' status
				{
     
					SetMark(r, c, unsolvedSudoku[r][c], 1);
					row[r]++;
					col[c]++;
					block[BlockNum(r, c)]++;
				}
			}
		}

DFS()
关键代码：

for (int i = 1; i < 10; i++)
	{
     
		if (!rowMark[r][i] && !colMark[c][i] && !blockMark[BlockNum(r, c)][i])
		{
     
			unsolvedSudoku[r][c] = i;
			SetMark(r, c, unsolvedSudoku[r][c], 1); //fill
			if (DFS(deep + 1))return true;
			SetMark(r, c, unsolvedSudoku[r][c], 0); //unfill
			unsolvedSudoku[r][c] = 0;
		}
	}

程序分析与改进

应用代码质量分析工具消除警告

利用VS2019自带的代码分析工具分析后

对应代码行：

198行：

if (num <= 0 || strlen(argv[2]) != int(log10(num)) + 1 || num > 1000000)

改后

if (num <= 0 || strlen(argv[2]) != double(log10(num)) + 1 || num > 1000000)

220行：

cout << "Used time = " << double(finish - start) / CLOCKS_PER_SEC << "s" << endl;

改后

cout << "Used time = " << (double(finish) - double(start)) / CLOCKS_PER_SEC << "s" << endl;

成功消除所有警告

应用代码性能分析工具提高程序性能

1.代码复用

在函数设计过程中，把需要多次调用的代码块写成了函数，并以函数的形式进行调用。同时将打印数独终局结果的函数和打印求解数独结果的函数合并为一个函数，通过参数标记的不同调用函数的不同部分，使得函数的功能更加清晰，代码的整体结构更为简洁。

2.输出改进

第一个版本的输出方式是在开始生成数独终局前，打开一个文件，每生成一行写入一次。
查询 cppreference.com ，结合代码分析出性能瓶颈主要为以下两点：

（1）每行结束都插入换行符，使用endl操纵符插入换行之后都会调用 flush() ，由于采用的是生成一行写入一行的 输出方式，所以频繁 调用flush() 耗费较多时间。
（2）生成一行写入一行的输出方式导致 basic_filebuf 为了维护文件位置会对指针进行频繁操作。文件在生成终局过程中始终保持打开，sync 函数耗费大量资源保持同步。

对 （1），不再在每行结束后插入endl，改为插入’\n’。
对 （2），更改 I/O 方式，不再生成一行写入一行，通过一个大的字符数组缓存所有要写入文件的字符，包括空格和换行符，在生成结束后一次性写入文件。

运行代码性能探查器进行CPU查询

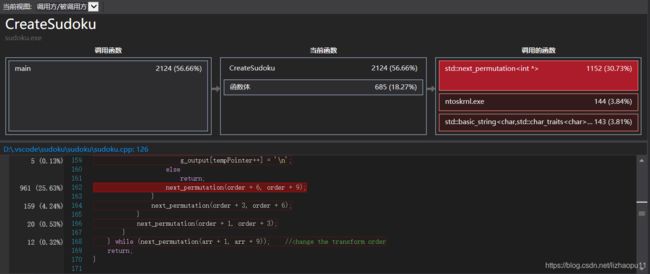
最耗时部分是 std::next_permutation 函数，这是用于生成下一个数字排列顺序的全排列函数，由于数独的生成主要依赖与数字顺序的变化和行列的交换，因此生成排列的函数调用次数较多，耗时符合预期。

实际耗费时间

PSP2.1	Personal Software Process Stages	预估耗时（min）	实际耗时（min）
Planning	计划	120	120
Estimate	估计这个任务需要多少时间	2250
Development	开发	1800
Analysis	需求分析（包括学习新技术）	30	30
Design Spec	生成设计文档	30	40
Design Review	设计复审（和同事审核审计文档）	10	20
Coding Standard	代码规范（为目前的开发制定合适的规范）	20	20
Design	具体设计	180	150
Coding	具体编码	1200	1000
Code Review	代码复审	120	120
Test	测试（自我测试，修改代码，提交修改）	120	60
Reporting	报告	240	240
Test Report	测试报告	30	40
Size Measurement	计算工作量	30	30
Postmortem & Process Improvement Plan	事后总结，并提出过程改进计划	120	150
	合计	2250	2020