CompareTo 基于的排序算法
CompareTo 基于的排序算法(高级排序)
这个是今天学习MapReduce时发现的,自定义类后实现了WritableComparable<>接口后实现了接口中的compareTo方法,返回>1或者<1则会自动进行排序的方法。
然后特别好奇,查了查,学习下做一个总结。
首先说明 实现CompareTo方法的是使用了Collections.sort()和Arrays.sort()底层得算法,是timsort算法,插入排序和归并排序的高级合并 .
详情:https://blog.csdn.net/yangzhongblog/article/details/8184707
而这2个方法在底层实现时,使用到了object1.compareTo(object2)这种方法进行判断谁大谁小,从而调整数组,最终给你返回有序的集合,两个方法的排序算法实现有归并排序和快速排序。
详细将一下:归并排序是属于递归中的一种,而快速排序是是属于高级排序的,与其同时的 还有希尔排序,划分,基数排序。但最常用的还是快速排序。这里详解一下技术排序,归并排序我则在记录递归是将其一并总结。所以我来详解一下这个高级排序
高级排序
希尔排序:
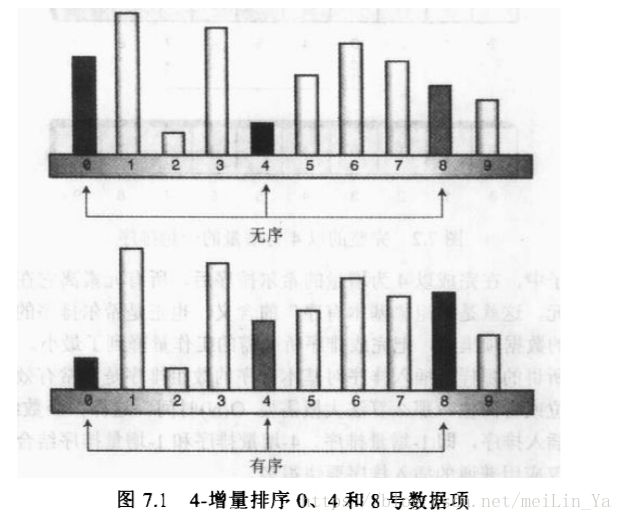
n-增量排序:通过加大插入排序中的元素之间的间隔。n:是指元素之间的间隔几个元素
我们来看一下主要的 4- 增量排序的放的排序过程。所有元素在离它最终的有序序列中的位置相差不到两个单元,做到了数据的基本有序,希尔则是做到了数据的基本有序,通过创建这种交错的内部有序的数据项集合,把完成排序所需的工作降调到最小
那么我们来研究一下这个间隔,这个间隔到底是使用多少为合适,可以将希尔的作用发挥到及至。以及间隔的选用。
间隔是通过数组得到大小进行变化的。比如1000个数据,间隔则为364-->121-->40-->13-->4-->1 这个间隔序列是通过递归计算出来的
谈希尔适合的排序环境:
这里是我的个人见解,如有更好的见解,欢迎一起讨论!!!
希尔排序适合中量数据的基本有序排序,少量数据使用插入排序进行更为稳定。
走开走开~~代码来了
package AdvancedRanking.ShellSort;
public class ArraySh {
//数组
private long[] theArray;
//数组长度
private int nElems;
public ArraySh(int max) {
theArray = new long[max];
nElems = 0;
}
public void insert(long value) {
theArray[nElems] = value;
nElems++;
}
public void display() {
System.out.print("A=");
for (int j = 0; j < nElems; j++) {
System.out.print(theArray[j] + " ");
}
System.out.println("");
}
public void shellSort() {
int inner, outer;
long temp;
//初始时元素之间的间隔
int h = 1;
while (h <= nElems / 3) {
h = h * 3 + 1;
}
while (h > 0) {
for (outer = h; outer < nElems; outer++) {
temp = theArray[outer];
inner = outer;
while (inner > h - 1 && theArray[inner - h] >= temp) {
theArray[inner] = theArray[inner - h];
System.out.println(theArray[inner]);
inner -= h;
}
theArray[inner] = temp;
}
//结束时元素之间的间隔
h = (h - 1) / 3;
}
}
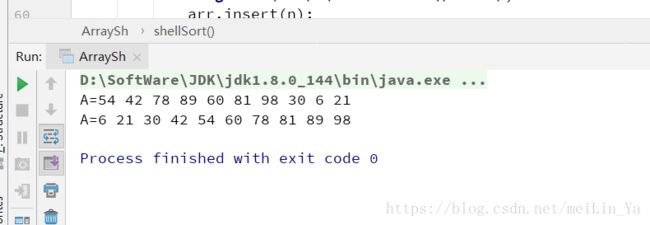
public static void main(String[] args) {
int maxSize = 10;
ArraySh arr = new ArraySh(maxSize);
for (int j = 0; j < maxSize; j++) {
long n = (int) (Math.random() * 99);
arr.insert(n);
}
arr.display();
arr.shellSort();
arr.display();
}
}
希尔排序的交换位置不是直接复制粘贴,它会一直于前面的那个数比较知道那个数小于枢纽(temp)时,如果没有小于枢纽时,他会将前面的那个数复制,占位,然后于下一个数比较。才会将枢纽的复制到它的位置。如果看不懂我说的话就DEBUG一下把,之后你就可以一目了然,知道我在说什么了。
二.划分
package AdvancedRanking.PartitionSort;
public class ArrayPar {
private long[] theArray;
private int nElems;
public ArrayPar(int max) {
theArray = new long[max];
nElems = 0;
}
public void insert(long value) {
theArray[nElems] = value;
nElems++;
}
public int size() {
return nElems;
}
public void display() {
System.out.print("A=");
for (int j = 0; j < nElems; j++) {
System.out.print(theArray[j] + " ");
}
System.out.println("");
}
public int partitionIt(int left, int right, long pivot) {
int leftPtr = left - 1;
int rightPtr = right + 1;
while (true) {
//最大得
while (leftPtr < right && theArray[++leftPtr] > pivot) ;
//最小的
while (rightPtr > left && theArray[--rightPtr] > pivot) ;
if (leftPtr > rightPtr) {
break;
} else {
swap(leftPtr, rightPtr);
}
}
return leftPtr;
}
public void swap(int dex1, int dex2) {
long temp;
temp = theArray[dex1];
theArray[dex1] = theArray[dex2];
theArray[dex2] = temp;
}
public static void main(String[] args) {
int maxSize = 10;
ArrayPar arr = new ArrayPar(maxSize);
for (int j = 0; j < maxSize; j++) {
long n = (int) (Math.random() * 199);
arr.insert(n);
}
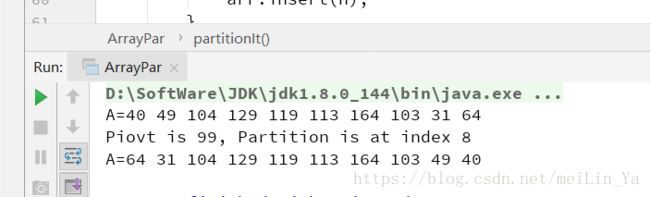
arr.display();
long piovt = 99;
System.out.print("Piovt is " + piovt);
int size = arr.size();
int partDex = arr.partitionIt(0, size - 1, piovt);
System.out.println(", Partition is at index " + partDex);
arr.display();
}
}
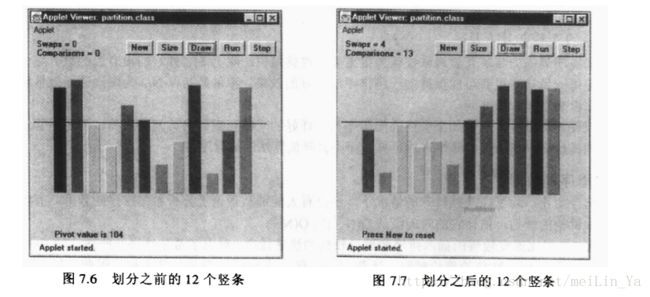
划分算法是由两个指针开始工作的,两个指针分别指向数据的两头leftPtr初始化是在第一个数据项的左边的一位,rightPtr是在最后一个数据项的右边一位。他们分别要-1 +1
//找小于于piovt
while (leftPtr < right && theArray[++leftPtr] > pivot) ;
//找小于pivot
while (rightPtr > left && theArray[--rightPtr] > pivot) ;当数据theArray[++leftPtr]和theArray[--rightPtr]>pivot时,它会一直++或者--下去,知道找到那个人>pivot数,然后进行交换实现基本排序。还是老话,看不懂我说什么就DEBUG一下。
划分算法运行时间为O(N),他其中的piovt枢纽,根据枢纽来移动指针和交换数据位置,虽然交换次数少,但是比较次数多。100个数大约交换25次,102次的比较。
三.快速排序
毫无疑问,快排时最流行的排序算法,但是多数情况下,快排都最快。执行时间为O(N*logN)(这只对内部排序和随机存储器内的排序而言,对于磁盘中文件中的数据进行排序可能更好)。
递归的快速排序算法:
package AdvancedRanking;
public class FastSorting {
private long[] theArray;
private int nElems;
public FastSorting(int max) {
theArray = new long[max];
nElems = 0;
}
public void insert(long value) {
theArray[nElems] = value;
nElems++;
}
public void display() {
System.out.print("A=");
for (int j = 0; j < nElems; j++) {
System.out.print(theArray[j] + " ");
}
System.out.println("");
}
public void quickSort() {
recQuickSort(0, nElems - 1);
}
public void recQuickSort(int left, int right) {
if (right - left <= 0) {
return;
} else {
long pivot = theArray[right];
int partition = partition(left, right, pivot);
recQuickSort(left, partition - 1);
recQuickSort(partition + 1, right);
}
}
public int partition(int left, int right, long pivot) {
int leftPtr = left - 1;
int rightPtr = right;
while (true) {
while (theArray[++leftPtr] < pivot) ;
while (rightPtr > 0 && theArray[--rightPtr] > pivot) ;
if (leftPtr >= rightPtr) {
break;
} else {
swap(leftPtr, rightPtr);
}
}
swap(leftPtr, right);
return leftPtr;
}
public void swap(int dex1, int dex2) {
long temp = theArray[dex1];
theArray[dex1] = theArray[dex2];
theArray[dex2] = temp;
}
public static void main(String[] args) {
int maxSize = 16;
FastSorting arr = new FastSorting(maxSize);
for (int j = 0; j < maxSize; j++) {
long n = (int) (Math.random() * 99);
arr.insert(n);
}
arr.display();
arr.quickSort();
arr.display();
}
}代码看不懂得时候调试下吧,想知道更多也调试一下吧,ideaDEBUG超级牛逼的,那功能是eclipse比不了的。但eclipse也是不错的。
感谢idea开发者。谢谢!!
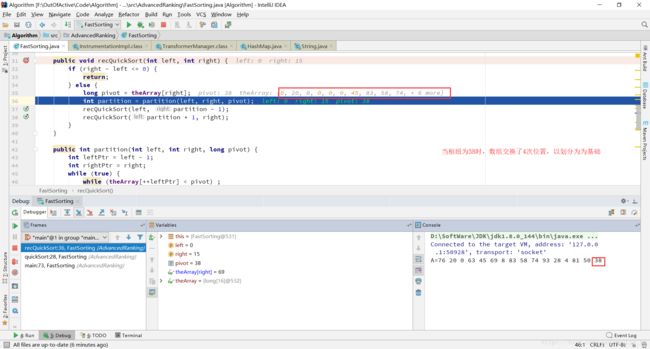
这里的pivot的选择是通过不是随意定的,一般选择最右面的枢纽,当第一波pivot比较完后,第一次的枢纽的位置也确定了。第一个枢纽的前一个数则为下一个枢纽。
那么这样我就将一个数组多次划分为2个部分进行比较,划分到不能划分为止。如下图
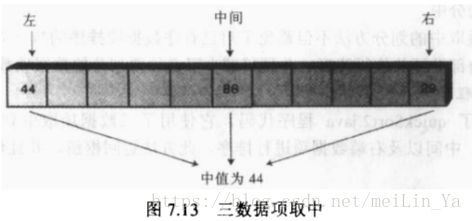
这里的枢纽位置是选择在最右端,入股数据是任意排序,那么这个选择不会太坏,如果,因为通常情况下枢纽不会太kao'j数组的两端,但是,当数据有序或者捏徐我们则选择枢纽时使用“三数据项中取”划分。
a
代码测试三数据项中取划分的好处。
package AdvancedRanking.FastSorting;
public class ArrayIns2 {
private long[] theArray;
private int nElems;
public ArrayIns2(int max) {
theArray = new long[max];
nElems = 0;
}
public void insert(long value) {
theArray[nElems] = value;
nElems++;
}
public void display() {
System.out.print("A=");
for (int j = 0; j < nElems; j++) {
System.out.print(theArray[j] + " ");
}
System.out.println("");
}
public void quickSort() {
recQuickSort(0, nElems - 1);
}
public void recQuickSort(int left, int right) {
int size = right - left + 1;
//大划分
if (size <= 3) {
manualSort(left, right);
} else {
//获取枢纽
long median = medianOf3(left, right);
//获取划分
int partition = partitionIt(left, right, median);
recQuickSort(left, partition - 1);
recQuickSort(partition + 1, right);
}
}
//获取枢纽并将三项排序
public long medianOf3(int left, int right) {
int center = (left + right) / 2;
if (theArray[left] > theArray[center]) {
swap(left, center);
}
if (theArray[left] > theArray[right]) {
swap(left, right);
}
if (theArray[center] > theArray[right]) {
swap(center, right);
}
swap(center, right - 1);
System.out.print(theArray[right - 1]+" ");
return theArray[right - 1];
}
//划分比较
public int partitionIt(int left, int right, long pivot) {
int leftPtr = left;
int rightPtr = right - 1;
while (true) {
while (theArray[++leftPtr] < pivot) ;
while (theArray[--rightPtr] > pivot) ;
if (leftPtr >= rightPtr) {
break;
} else {
swap(leftPtr, rightPtr);
}
}
swap(leftPtr, right - 1);
return leftPtr;
}
public void swap(int dex1, int dex2) {
long temp = theArray[dex1];
theArray[dex1] = theArray[dex2];
theArray[dex2] = temp;
}
//小划分,当数据小于3个或者更少的数据项的子数组进行排序
public void manualSort(int left, int right) {
int size = right - left + 1;
if (size <= 1)
return;
if (size == 2) {
if (theArray[left] > theArray[right])
swap(left, right);
return;
} else {
if (theArray[left] > theArray[right - 1])
swap(left, right - 1);
if (theArray[left] > theArray[right])
swap(left, right);
if (theArray[right - 1] > theArray[right])
swap(right - 1, right);
}
}
public static void main(String[] args) {
int maxSize = 16;
ArrayIns2 arr = new ArrayIns2(maxSize);
for (int j = 0; j < maxSize; j++) {
long n = (int) (Math.random() * 99);
arr.insert(n);
}
arr.display();
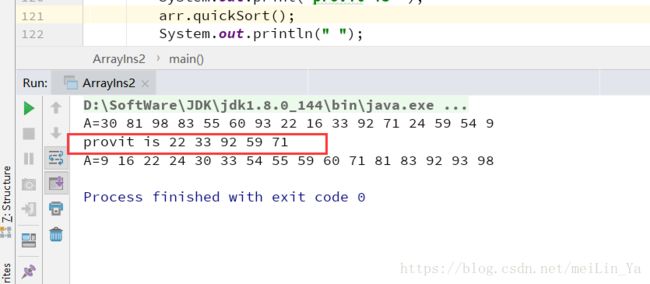
System.out.print("provit is ");
arr.quickSort();
System.out.println(" ");
arr.display();
}
}好处:
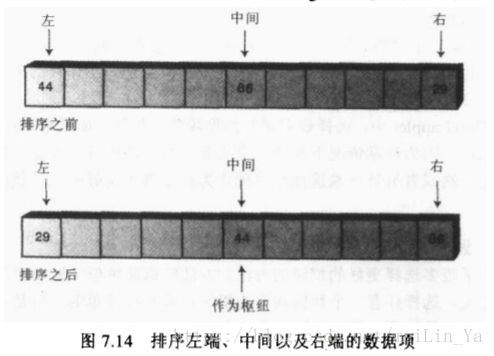
1.三数据项的中只数据项比查找出所有数据项快很多,同时可以有效的避免了在数据已经有序或者逆序的情况下,选择最大或者最小的数据作为枢纽。但是在三项中排列和选择枢纽的方法又是很低效的。
2.三个数据项已经排号序,while循环中不用判断rightPtr>left的测试。
3.左端,中间以及右端数据项排序之后,划分过程不需要再考虑着三个数据项了,从left+1和right-1开始·
快排3,处理小划分
//小划分,当数据小于3个或者更少的数据项的子数组进行排序
public void insertionSort(int left, int right) {
int in, out;
for (out = left + 1; out <= right; out++) {
long temp = theArray[out];
in = out;
while (in > left && theArray[in - 1] >= temp) {
theArray[in] = theArray[in - 1];
--in;
}
theArray[in]=temp;
}
}四.基数排序
基数排序和前面的排序算发不同,前面是对简单数值的型关键字的排序小狐狸,基数排序是吧关键字拆分成数字喂,并且对按数字位的值对数据项进行排序。最奇怪的是技术排序不需要比较。
技术排序所需的存储空间是快速排序的二倍。
总结:
1.希尔排序讲增量应用到插入排序种,然后逐渐缩小增量。
2.n-增量排序表示每隔n个元素进行排序。
3.被常用的间隔列或者间距序列决定了希尔排序的排序间隔
4.常用的间隔序列是由递归表达式h=3*h+1生成的,h的初始值为1.
5.一个容纳了1000个数据项的数组,对它进行希尔排序可以是间隔序列364,121,40,13,4,最后是增量
6.希尔排序比快速排序慢
7.划分算法内部的while循环需要额外的检测,防止数组下标越界。
8.划分中,在各自的while虚幻中的两个数据此阿布指针,分别从数组的两端开始,相向移动,查询需要交换数据选项。
9.快速排序的简单版中,总是由子数组的最右端的数据项作为枢纽。
10.快速排序划分一个数组,然后递归调用自身,对划分得到的两个子数组进行快速排序。