2019CCPC网络赛部分题解
这场锅最大的应该是我吧。。。一个半小时的时候我已经写完了08的正解,然而突发奇想也没造数据就把自己叉了,然后带着学弟想了俩小时这道傻逼题。。。
三道签到题我都没看题,学弟一个人写的;wtw不在学校,抽空回酒店写了03,原话“这道题我看了30s就会了”;我的本场唯一贡献08,加上一大段时间的负输出。
最后五题滚粗有点难受,有些题压根没时间搞。。。
1002 array
这道题似乎做法很多,我最初以为必须要主席树,就放弃思考了。。。
说下set+线段树的做法吧。
首先因为k<=n,可知答案必定在[k,n+1]中。
对于操作1,将某个位置的值加上1e7其实和删去原来的值没有差别,因为n<=1e5,加上1e7后就不可能成为答案。
对于操作2,查询未在序列[1,r]位置出现过的,大于等于k的最小值。
因为给的初始序列是一个排列,令n+1位置处的值为n+1,那么可能的答案其实就是:
1. [1,r]中删去的(如果有的话)恰好大于等于k的值;
2. [r+1,n+1]所有值中(不论是否删去)恰好大于等于k的值。
那么其实就等价于
1. [1,n+1]中删去的恰好大于等于k的值;
2. [r+1,n+1]所有值中恰好大于等于k的值。
这样就很容易维护了。
对于1,将所有删去的位置的数都放进set中,每次通过二分查找到一个恰好大于等于k的值。
对于2,建一棵权值线段树,存每个值所在的下标,维护区间最大值。可知需要在[k,n+1]区间找到一个下标大于r的最左端的位置,那么查询的时候就可以在线段树上进行二分。
将得到的两个值取较小值即可,时间复杂度O(nlogn)。
AC代码:
#include
using namespace std;
#define ls (rt<<1)
#define rs (rt<<1|1)
const int maxn=1e5+5;
struct node{
int l,r,maxx;
}Q[maxn<<2];
set st;
set::iterator it;
int T,n,m;
int op,p,r,k,ans,a[maxn],b[maxn];
void build(int rt,int l,int r){
Q[rt].l=l,Q[rt].r=r;
if(Q[rt].l==Q[rt].r){
Q[rt].maxx=b[l];return;
}
int mid=(Q[rt].l+Q[rt].r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
Q[rt].maxx=max(Q[ls].maxx,Q[rs].maxx);
}
int query(int rt,int l,int p){//[l,n+1]中最小且位置大于等于p的
if(Q[rt].l==Q[rt].r){
if(Q[rt].maxx>=p) return Q[rt].l;
else return 0;
}
int mid=(Q[rt].l+Q[rt].r)>>1;
if(mid=p) res=query(ls,l,p);
if(res==0&&Q[rs].maxx>=p) res=query(rs,l,p);
return res;
}
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
ans=0;
st.clear();
for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[a[i]]=i;
b[n+1]=n+1;
build(1,1,n+1);
for(int i=1;i<=m;i++){
scanf("%d",&op);
if(op==1){
scanf("%d",&p);
p^=ans;
st.insert(a[p]);
}
else{
scanf("%d %d",&r,&k);
r^=ans,k^=ans;
it=st.lower_bound(k);
if(it!=st.end()) ans=*it;
else ans=n+1;
ans=min(ans,query(1,k,r+1));
cout< 1004 Path
不会算这个复杂度,我觉得自己的做法是个暴力。。。
结束前二十多分钟想了下这道题,只能想到用multiset维护maxk条路径长度暴力。想莽一发但是没写完。
后来写完就T了,因为maxk(k的最大值)直接设的5e4,改成每组真正的maxk之后就过了。
先将每个点的邻接边按边长排序,可能算是一个小优化。
将路径按长度排序,先把所有单独的路径放入multiset,然后取当前的最短的路径进行更新,若路径总数小于maxk,无脑放入当前的multiset;若路径总数已经达到maxk且更新后的路径已经比最长的路径还长,则不用继续更新,将当前路径放入另一个multiset中;若路径总数已经达到maxk且更新后的路径比最长的路径短,将最长的路径踢出去,把更新的路径放入当前multiset;若当前路径的所有后继已更新完,也放入另一个multiset中。
最后需要的maxk条路径都会在另一个multiset中。时间复杂度未知。
AC代码:
#include
using namespace std;
#define ll long long
const int maxn=5e4+5;
struct node{
int u;
ll w;
node(int _u=0,ll _w=0):u(_u),w(_w){}
bool operator <(const node &p)const{
return w mst,mst1;
multiset::iterator it,it1;
int n,m,q,maxk,k[maxn],u,v,w,T;
vector G[maxn];
ll ans[maxn];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d %d",&n,&m,&q);
for(int i=1;i<=n;i++) G[i].clear();
maxk=0;
mst.clear();
mst1.clear();
for(int i=1;i<=m;i++){
scanf("%d %d %d",&u,&v,&w);
G[u].push_back(node(v,w));
mst.insert(node(v,w));
}
for(int i=1;i<=n;i++) sort(G[i].begin(),G[i].end());
for(int i=1;i<=q;i++){
scanf("%d",&k[i]);
maxk=max(maxk,k[i]);
}
while(mst.size()){
it=mst.begin();
for(node tt:G[(*it).u]){
tmp.u=tt.u;
tmp.w=tt.w+(*it).w;
if(mst.size()+mst1.size()=(*it1).w) break;
else{
mst.erase(it1);
mst.insert(tmp);
}
}
}
mst1.insert(*it);
mst.erase(it);
}
u=0;
for(it=mst1.begin();it!=mst1.end();it++) ans[++u]=(*it).w;
for(int i=1;i<=q;i++) cout< 1005 huntian oy
似乎是去年多校的时候见到了这个式子,就记在了模板里,晚上补题一看到题目就翻到了。
因为a、b互质,所以所求为:
接下来进行莫比乌斯反演,易知所求为f(1)
所以有
则
后面那部分显然可以数论分块,因此需要想办法求
开头我把这玩意当成![]() (二者的狄雷克利卷积)了,显然不是。。。前缀和不好求,那么考虑对
(二者的狄雷克利卷积)了,显然不是。。。前缀和不好求,那么考虑对![]() 进行狄雷克利卷积,凑出前缀和好求的积性函数。
进行狄雷克利卷积,凑出前缀和好求的积性函数。
这里可以卷个id(i),则有
因此有
即
后面那部分可以数论分块,所以可以用杜教筛来求S(n)。
至此,本题就解决了。线性筛预处理前![]() 的S(n),则杜教筛时间复杂度为
的S(n),则杜教筛时间复杂度为![]() 。
。
AC代码:
#include
using namespace std;
#define ll long long
const int mod=1e9+7;
const int maxn=1e6+5;
int T,n,a,b;
int prime[maxn],cnt,mu[maxn];
bool notprime[maxn];
inline void init(){
notprime[1]=1;
mu[1]=1;
for(int i=2;i ump;
int S(int x){
if(x>=1;
a=a*1ll*a%mod;
}
return res;
}
int inv=qpow(6,mod-2);
int main(){
init();
scanf("%d",&T);
while(T--){
scanf("%d %d %d",&n,&a,&b);
ll ans=0;
for(int l=1,r,tt;l<=n;l=r+1){
tt=n/l;
r=n/tt;
ans=(ans+(S(r)-S(l-1))*((tt-1)*1ll*tt%mod*(tt+1)%mod*inv%mod))%mod;
}
if(ans<0) ans+=mod;
cout< 1008 Fishing Master
令sumk=n*k,sumt=sum(ti)+k,分别为初始的钓鱼的结束时间和炖鱼的结束时间。
考虑到炖一条鱼的时候渔夫有两种选择,一种是多等待ti%k,使得钓鱼的最后结束时间推后;另一种是浪费k-ti%k,使炖鱼的最后结束时间推后。我们需要的是使得两者的最大值最小。
因为ti%k从小往大的时候k-ti%k必然从大往小,如果设定一个最终结束时间的话,就会存在贪心策略,多等待的时间一定是按ti%k从小往大选,浪费的时间也一定是按k-ti%k从小往大选。
对每个ti处理出这两个数,然后按其中一个排序。比如按ti%k从小到大排序。
二分最终结束时间,贪心的从小到大选择ti%k,直到sumk再增加就会超过最终结束时间,剩下的就都认为是将k-ti%k加给sumt。若二者都满足小于等于最终结束时间,则缩小二分上界;否则增大下界。
初始的二分下界可以为max(sumk,sumt),上界可以为sumk+sumt-k。
时间复杂度O(nlogn)。
AC代码:
#include
using namespace std;
#define ll long long
const int maxn=1e5+5;
int T,t[maxn],k,n,cnt;
struct node{
int a,b;
bool operator<(const node &p)const{return a 写题解的时候常常可以产生新的想法。。。对于本题,既然贪心策略存在,那么其实可以不用二分。
最后二分部分改为:正着对ti%k做一遍前缀和,再反着将k-ti%k相加,考虑以当前位置为分界时的最终结束时间,维护最小值即可。
当然,因为要排序,时间复杂度其实不变,还是O(nlogn),只是常数小。
AC代码:
#include
using namespace std;
#define ll long long
const int maxn=1e5+5;
int T,t[maxn],k,n,cnt;
struct node{
int a,b;
bool operator<(const node &p)const{return a=1;i--){
s+=c[i].b;
ans=min(ans,max(sumk+sum[i-1],s+sumt));
}
cout<
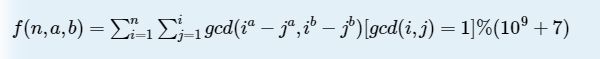
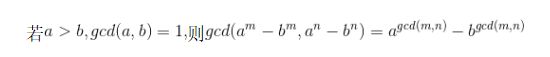
![\sum_{i=1}^{n}\sum_{j=1}^{i}(i^{gcd(a,b)}-j^{gcd(a,b)})[gcd(i,j)=1]=\sum_{i=1}^{n}\sum_{j=1}^{i}(i-j)[gcd(i,j)=1]](http://img.e-com-net.com/image/info8/99a7dda06a254577bb11c1834f67e4d0.gif)
![f(d)=\sum_{i=1}^{n}\sum_{j=1}^{i}(i-j)[gcd(i,j)=d]=d\sum_{i=1}^{\left \lfloor \frac{n}{d}\right \rfloor}\sum_{j=1}^{i}(i-j)[gcd(i,j)=1]](http://img.e-com-net.com/image/info8/11cd2875663747b58cead2da06aa7d8e.gif)
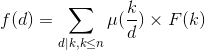
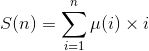
![(\mu(i)\times i) *id(i)=\sum_{d|i}\mu(d)\times d\times \frac{i}{d}=i\sum_{d|i}\mu(i)=i[i=1]](http://img.e-com-net.com/image/info8/7d854496ba9e4b23ae7cd1747ff6ba8a.gif)