【cs224n-2019学习笔记-2】notes01-wordvecs1: Introduction, SVD and Word2Vec

本文首先介绍了自然语言处理(NLP)的概念和NLP目前面临的问题，然后继续讨论了将单词表示为数字向量的概念，最后讨论了常用的词向量设计方法。

关键词：自然语言处理，词向量，奇异值分解，Skip-gram，CBOW，negative Sampling，Hierarchical Softmax，Word2Vec。

1.自然语言处理概论

首先对什么是自然语言处理进行一般性讨论。

1.1 NLP有什么特别之处？

人类（自然）语言有什么特别之处？人类语言是一个专门用来表达意义(meaning)的系统，并且它不是由任何形式的物理表现所产生的。这样，它与视觉或任何其他机器学习任务都有很大的不同。

大多数单词只是一个非语言实体的符号：单词是一个能指(signifier)，映射到一个所指(signified)(想法或事物)。

例如，“火箭”一词指的是火箭的概念，并通过引申可以指定火箭的实例。当我们使用单词和字母来表达信号时，有一些例外，比如“Whooompaa”。除此之外，语言的符号可以用多种方式编码：声音、手势、文字等，这些编码通过连续的信号传送到大脑，大脑本身似乎以连续的方式对事物进行编码。(在语言哲学和语言学方面已经做了大量的工作，使人类语言概念化，并将词语和它们的指称、意义等区分开来。其中，可以参阅Wittgenstein, Frege, Russell and Mill等人的著作。)

• （对于Whooompaa这地方没有看懂）
• 注释：自然语言是一个离散/符号/范畴系统。

1.2 任务示例

NLP中有不同层次的任务，从语音处理到语义解释和语篇处理。为了完成某些任务，NLP的目标是能够设计算法使得计算机为了能够“理解”自然语言。任务示例的难度不同：

• Easy
  • 拼写检查
  • 关键词搜索
  • 寻找同义词
• Medium
  • 解析网站、文档等信息
• Hard
  • 机器翻译(如，中英翻译)
  • 语义分析(如，查询语句(n)的含义是什么？)
  • 共指(如，在给定的文件中，“他”、“它”分别指的是什么)
  • 问答(QA)

1.3 如何表示单词

在所有的NLP任务中，首要的共同点是我们如何将单词表示为任何模型的输入。许多早期的NLP工作都将单词视为原子符号，在这里我们不讨论。要在大多数NLP任务中表现出色，我们首先需要对单词之间的相似性和差异性有一些概念。使用词向量，我们可以很容易地将这种能力(相似性和差异性概念)编码到向量本身（使用诸如Jaccard、Cosine、Euclidean等距离度量）

2.词向量

在英语中大概有1300万个token，但是它们之间是完全不相关的吗？Feline to cat,hotel to motel?我认为不是。因此，我们希望将每个word token编码成向量，这个向量表示某种“单词”空间中的某个点。这是最重要的一个原因，但是最直观的原因是，也许实际上存在一些N维空间(如N<<1300万)，这个N维空间足以编码我们语言的所有语义。每个维度都会编码一些我们用语音传递的意思。例如，语义维度可能表示时态(过去 vs. 现在 vs. 未来)，计数(单数 vs. 复数)，和性别(男性 vs. 女性)。

因此，我们来深入研究一下我们的第一个词向量，可以说是最简单的，独热向量(ont-hot vector)：用一个${\mathbb{R}}^{|V|\ast 1}$的向量表示一个单词，向量中与该词在词表中的索引位置对应的位置为1，其他位置为0。其中，|V|是词表的大小。此类编码的词向量如下所示：
在独热向量中，我们把每个单词都表示为了一个完全独立的实体。正如我们之前讨论过的，这种单词表示并没有直接给我们任何关于相似性的概念。比如：
$$(w^{hotel}{)}^T{w}^{motel}=(w^{hotel}{)}^T{w}^{cat}=0$$

因此或许我们可以尝试将这个空间的大小从${\mathbb{R}}^{|V|}$减小到更小一些，从而找到一个可以编码单词之间关系的子空间。

• 指称语义(Denotational semantics)：将一个idea表示为一个符号(一个词或一个独热向量)。它是稀疏(sparse)的，无法捕捉到相似度。并且这是一种“localist” representation。

3.基于SVD的方法

对于这类寻找word embeddings(也称为word vectors)的方法，我们首先大量数据集上循环遍历，并以某种形式的矩阵X累积单词的共现计数，然后对X进行奇异值分解得到$US{V}^T$分解。然后我们使用U的行作为字典中所有单词的词嵌入。下面讨论几种X的选择。

3.1 Word-Document 矩阵

作为我们的第一次尝试，我们大胆地推测：相关的词回经常出现在同一个文档中。例如，银行、债券、股票、货币等可能会一起出现，但是银行、章鱼、香蕉和曲棍球等可能不会一直一起出现。我们使用这个事实去构建一个word-document矩阵X，X的构造方式如下：循环处理数十亿个document，每次word i出现在document j中，$X_{ij}$加1。很显然，这是一个非常大的矩阵(${\mathbb{R}}^{|V|\ast M}$)，并且它随document数量(M)而变化。所以也许我们可以尝试更好的方法。

• 分布式语义(Distributional semantics):根据一个词通常出现的上下文来表示其meaning的概念。它很密集(dense)，并且能更好地捕捉相似性。

3.2 基于窗口(window)的共现(Co-occurrence)矩阵

3.1中同样的逻辑也适用于这里，矩阵X存储单词的共现，从而成为关联矩阵(affinity matrix)。在这种方法中，在一个特定大小的窗口中，我们计算每个单词出现在我们感兴趣单词周围的次数。我们计算语料库(corpus)中所有单词的这种次数。下面是一个例子，语料库中只包含三个句子，window size = 1：

1. I enjoy flying.
2. I like NLP.
3. I like deep learning.

则最终的计数矩阵为：

3.3 将SVD应用到共现矩阵中

现在我们在X上应用SVD，观察奇异值(S矩阵中的对角线项)，并根据所捕获的期望百分比方差在某个索引k处将其截断：
$$\frac{{\sum }_{i=1}^k{\sigma }_i}{{\sum }_{i=1}^{|V|}{\sigma }_i}$$
然后我们将子矩阵$U_{1:|V|,1:k}$作为我们word embedding的矩阵。这就给了我们词表中每个词的k维表示。


使用word-word共现矩阵：

• 生成一个|V|*|V|的共现矩阵X
• 将SVD应用到X得到$X=US{V}^T$
• 选择U的前k列以获得k维词向量
• $\frac{{\sum }_{i=1}^k{\sigma }_i}{{\sum }_{i=1}^{|V|}{\sigma }_i}$表示前k维捕获的方差

以上两种方法都为我们提供了足以编码语义和句法(词性)信息的词向量，但是还存在许多其他问题：

• 矩阵的维度变化非常频繁(新词的添加非常频繁，语料库的大小也随之变化)
• 矩阵非常稀疏，因为词表中的大多数单词不会同时出现
• 矩阵通常是高维的($\approx 10^6\ast 10^6$)
• 二次训练成本(比如，使用SVD)
• Requires the incorporation of some hacks on X to account for the drastic imbalance in word frequency解决词频严重不平衡的问题

上述问题的一些解决方案：

• 忽略虚词，如the、he、has等
• 使用一个渐变(ram)窗口，比如，根据文档中单词之间的距离加权共现计数
• 使用皮尔逊相关稀疏并将负计数设置为0，而不是使用原始计数

注释：

• 基于SVD的方法不能很好地适应大矩阵，并且很难合并新词或新文档。m*n的矩阵的计算量为$O(m{n}^2)$
• 然而，基于计数的方法有效地利用了统计信息

正如下面我们会看到的，基于迭代的方法以一种更优雅的方式解决了许多上述问题。

4.基于迭代的方法-Word2vec

让我们退后一步，尝试一种新方法。我们可以尝试创建一个模型，该模型一次学习一个迭代，并最终能够根据给定的上下文对单词的概率进行编码，而不是计算和存储一些大型数据集(可能是数十亿句子)的全局信息。

其思想是设计一个参数为词向量的模型，然后基于一定的目标训练模型。在每次迭代中，我们运行模型、评估错误，并遵循更新规则进行参数更新，该规则会惩罚导致错误的模型参数。因此，我们就学习到了词向量。这是一个可以追溯到1986年的古老想法。我们称这种方法为反向传播(backpropagating)错误( [Rumelhart et al., 1988])。模型和任务越简单，训练速度就越快。

已有一些方法被尝试。[Collobert et al., 2011] 为NLP设计了一些模型，其第一步是将每个词转换成一个向量。对每一个特殊任务(命名实体识别、词性标注等)，他们不仅训练模型的参数，也训练了词向量，取得了很好的性能，同时计算出了很棒的词向量。其他一些有趣的读物如 [Bengio et al., 2003]。

在本课程中，我们将介绍一种更简单、更新的概率方法，作者是[Mikolov et al., 2013]：word2vec。Word2vec是一个软件包，包括：

• 两种算法：continuous bag-of-words(CBOW)和skip-gram。
  • CBOW的目标是根据上下文预测中心词向量
  • Skip-gram则相反，根据中心词预测上下文词的分布(概率)
• 两种训练方法：negative sampling和hierarchical sofrmax。
  • 负采样：通过对负例进行采样来定义目标
  • 层次softmax：使用有效的树结构计算所有词汇的概率来定义目标

注释：

• 有关Word2vec的注释： https://myndbook.com/view/4900
• Word2vec的详细总结可见：[Rong, 2014]
• 基于迭代的方法一次捕获一个单词的共现，而不是像SVD那样直接捕获所有的共现计数
• Word2vec模型依赖于语言学中一个非常重要的假设，即分布相似，也就是相似的词有相似的上下文。

4.1 语言模型(Unigrams、Bigrams等)

首先，我们需要创建一个模型，该模型将概率分配给一系列tokens。让我们从一个例子开始：

• “The cat jumped over the puddle.”

一个好的语言模型会给这个句子一个很高的概率，因为这是一个在句法和语义上完全有效的句子。同样的，"stock boil fish is toy"这句话的概率应该很低，因此它毫无意义。从数学上讲，我们可以把这个概率称为含有n个单词的任意给定序列：
$$P(w_1,w_2,...,w_n)$$

我们可以采用一元语言模型(unary language model)方法，通过假设单词的出现完全独立来分解这个概率：
$$P(w_1,w_2,...,w_n)=\prod _{i=1}^{n}P(w_i)$$

然而我们知道这有点可笑，因为我们知道下一个词是什么在很大程度上取决于前一个单词序列。这个愚蠢的例句可能会得到很高的分数。因此，也许我们可以让句子序列的概率取决于序列中一个单词和它旁边单词的两两概率。我们称之为二元模型(bigram model):
$$P(w_1,w_2,...,w_n)=\prod _{i=2}^{n}P(w_i|w_{i-1})$$

同样，这当然也有些naive，因为我们只关心自己与相邻的词对，而不是评价一个完整的句子，但正如我们将看到的，这种表示让我们走得很远。注意，在上下文大小为1的word-word矩阵中，我们基本上可以学到这些成对概率。但同样，这需要计算和存储关于一个庞大数据集的全局信息。

现在我们已经了解了如何考虑一系列有概率的token，让我们来看一些可以学习这些概率的示例模型。

tips:CBOW及Skip-gram模型关键符号：

• 每个词w有两个向量：
  • 当w为输入词时,用$v_w$向量表示
  • 当w为输出词时，用$u_w$向量表示
• CBOW,利用上下文词预测中心词，输入矩阵为$\nu \in {\mathbb{R}}^{n\ast |V|}$，输出矩阵为$\mu \in {\mathbb{R}}^{|V|\ast n}$
• Skip-gram模型，利用中心词预测上下文词，输入矩阵为$\nu \in {\mathbb{R}}^{n\ast |V|}$，输出矩阵为$\mu \in {\mathbb{R}}^{|V|\ast n}$

4.2 连续词袋模型(CBOW)

一种方法是将 {“The”, “cat”, ’over", “the’, “puddle”} 作为上下文，并从这些词能够预测或者生成中心词"jumped”。这种模型我们称之为连续词袋模型(CBOW)。

让我们更详细地讨论上面的CBOW模型。首先，设置已知参数，让模型中的已知参数为由一个个独热向量表示的句子。我们将用$x^{(c)}$表示输入独热向量或者上下文，输出为$y^{(c)}$。在CBOW模型中，因为我们只有一个输出，所以我们称之为y，它是已知中心词的独热向量表示。现在让我们定义模型中的未知参数。

我们创建了两个矩阵，$\nu \in {\mathbb{R}}^{n\ast |V|}$和$\mu \in {\mathbb{R}}^{|V|\ast n}。其中，n是一个任意值，用来定义嵌入空间的大小。$\nu$是\ast \ast 输入\ast \ast 词矩阵，因此当$\nu$的第i列是该模型的输入时，它是单词$w_i$的n维嵌入向量。同样，$\mu$是\ast \ast 输出\ast \ast 词矩阵，当$\mu$的第j行是模型的输出时，它是单词$w_j$的n维嵌入向量，我们将$\mu$的这一行标记为$\mu_j$。注意，实际上我们为每一个词$w_i$学习两个向量(即，输入词向量$v_i$，输出词向量$u_i$)。

CBOW模型：

• 从上下文预测中心词
• 对每个词，我们要学习两个向量
  • v:(输入向量)当这个词为上下文词
  • u:(输出向量)当这个词为中心词

CBOW模型的符号：

• $w_i$:词表V中的词i
• $\nu \in {\mathbb{R}}^{n\ast |V|}$:输入词矩阵。
• $v_i$:$\nu$的第i列，词$w_i$的输入向量表示。
• $\mu \in {\mathbb{R}}^{|V|\ast n}$:输出词矩阵。
• $u_i$:$\mu$的第i行，词$w_i$的输出向量表示。

我们将此模型的工作方式分解为以下步骤：
1.我们为窗口大小为m的上下文生成独热词向量：
$$(x^{(c-m)},...,x^{(c-1)},x^{(c+1)},...,x^{(c+m)}\in {\mathbb{R}}^{|V|})$$
2.我们得到上下文的嵌入词向量：
$$(v_{c-m}=\nu \ast x^{(c-m)},v_{c-m+1}=\nu \ast x^{(c-m+1)},...,v_{c+m}=\nu \ast x^{(c+m)}\in {\mathbb{R}}^n)$$
3.将第2步中得到的词向量取平均，得到
$$\hat{v}=\frac{v_{c-m}+v_{c-m+1}+...+v_{c+m}}{2m}\in {\mathbb{R}}^n$$
4.生成分数向量$z=\mu \ast \hat{v}\in {\mathbb{R}}^{|V|}$。由于相似向量的点积更高，为了达到较高的分数，它会把相似的词推的更近。
5.把分数向量变成概率分布$\hat{y}=softmax(z)\in {\mathbb{R}}^{|V|}$。
6.我们希望我们产生的概率分布$\hat{y}\in {\mathbb{R}}^{|V|}$与真实的概率分布$y\in {\mathbb{R}}^{|V|}$相匹配，这(y)恰好也是实际单词的独热向量。

• CBOW的工作原理及如何学习两个矩阵如下图所示：
  
• 勘误：上图中的矩阵形状描述有问题，前面矩阵也就是$\nu$的形状应该是$N\ast V$，后面矩阵也就是$\mu$的形状应该是$V\ast N$。

现在我们已经了解了，如果我们有一个$\nu$和$\mu$，我们的模型是如何工作的，那么我们如何学习这两个矩阵呢？我们需要建立一个目标函数。很多时候，当我们试图从真实的概率分布中学习概率分布时，我们会借助信息论来度量两个分布之间的距离。在这里，我们使用一个流行的距离/损失度量，交叉熵$H(\hat{y},y)$。

在离散情况下使用交叉熵的直观性可以从损失函数的公式推导出来：
$$H(\hat{y},y)=-\sum _{j=1}^{|V|}{y}_j\ast log({\hat{y}}_j)$$

让我们关注一下我们的实际情况，也就是y是一个独热向量。因此，我们知道上述损失函数可以简化为：
$$H(\hat{y},y)=-y_c\ast log({\hat{y}}_c)$$

在这个公式中，c是正确单词的独热向量中值为1的位置索引。

• 我们现在可以考虑这样的情况，我们的预测是完美的，${\hat{y}}_c=1$，然后我们可以计算$H(\hat{y},y)=-1\ast log(1)=0$。因此，对于一个完美的预测，我们没有面临惩罚(penalty)或者损失(loss)。
• 现在让我们考虑相反的情况，我们的预测非常糟糕，${\hat{y}}_c=0.01$，如前所述，我们可以计算我们的损失为$H(\hat{y},y)=-1\ast log(0.01)\approx 4.605$。因此我们可以看到，对于概率分布(probability distributions)，交叉熵为我们提供了一个很好的距离度量。

因此我们的优化目标就是：
$$\begin{array}{rl}minimizeJ& =-logP(w_c|w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m})\\ & =-logP(u_c|\hat{v})\\ & =-log\frac{exp(u_c^T\hat{v})}{{\sum }_{j=1}^{|V|}exp(u_j^T\hat{v})}\end{array}$$

然后使用随机梯度下降来更新所有相关的词向量$u_c$和$v_j$。

• 当$\hat{y}=y$时，$\hat{y}\to H(\hat{y},y)$最小；因此如果我们找到一个$\hat{y}$使得$H(\hat{y},y)$很接近最小值，也就是$\hat{y}\approx y$，这意味着我们的模型能够很好的预测中心词。
• 为了学习词向量($\nu$和$\mu$矩阵)，CBOW定义了一个度量模型预测中心词的能力的代价函数，然后，基于随机梯度下降，我们通过更新两个矩阵来优化损失函数。

4.3 Skip-gram模型

另一种方法是创建一个模型，该模型能够基于给定的中心词"jumped"，预测或生成周围词"The"、“cat”、“over”、 “the”、“puddle”，也就是"jumped"的上下文词。

现在来讨论一下上面的Skip-gram模型，设置大体上和CBOW相同，但是我们基本上交换了x和y，即CBOW的x现在是Skip-gram的y，反之亦然。输入的独热向量(中心词)，我们将用x表示(因为只有一个);输出向量表示为$y^{(i)}。对$\nu$和$\mu$的定义与CBOW中的相同。

Skip-gram模型：

• 根据中心词预测上下文词

Skip-gram模型的符号：

• $w_i$:词表V中的词i
• $\nu \in {\mathbb{R}}^{n\ast |V|}$:输入词矩阵
• $v_i$:$\nu$的第i列，词$w_i$的输入向量表示
• $\mu \in {\mathbb{R}}^{|V|\ast n}$:输出词矩阵
• $u_i$:$\mu$的第i行，词$w_i$的输出向量表示

我们将此模型的工作步骤分为以下6个步骤：
1.我们为中心词生成独热词向量：$x\in {\mathbb{R}}^{|V|}$
2.我们得到中心词的嵌入词向量：$v_c=\nu \ast x\in {\mathbb{R}}^n$
3.生成分数向量$z=\mu \ast v_c\in {\mathbb{R}}^{|V|}$。
5.把分数向量变成概率分$\hat{y}=softmax(z)\in {\mathbb{R}}^{|V|}$。注意，${\hat{y}}_{c-m},...,{\hat{y}}_{c-1},{\hat{y}}_{c-+1},...,{\hat{y}}_{c+m}$是每个上下文词向量的概率分布。
6.我们希望我们产生的概率分布与真实的概率分布，也就是$y_{c-m},...,y_{c-1},y_{c+1},...,y_{c+m}$，相匹配，这些恰好也是实际单词的独热向量。

• Skip-gram的工作原理及如何学习两个矩阵如下图所示：
  

• 勘误：上图中的矩阵形状描述有问题，前面矩阵也就是$\nu$的形状应该是$N\ast V$，后面矩阵也就是$\mu$的形状应该是$V\ast N$。

如在CBOW中一样，我们需要生成一个目标函数(损失函数)来评估模型。这里与CBOW的管家你区别是，我们调用一个朴素贝叶斯假设来分解概率。简单地说，它是一个很强的(naive)的条件独立假设。换句话说，我们假设，给定中心词，所有输出词之间都是完全独立的。于是：
$$\begin{array}{rl}minimizeJ& =-logP(w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m}|w_c)\\ & =-log\prod _{j=0,j\ne m}^{2m}P(w_{c-m+j}|w_c)\\ & =-log\prod _{j=0,j\ne m}^{2m}P(u_{c-m+j}|v_c)\\ & =-log\prod _{j=0,j\ne m}^{2m}\frac{exp(u_{c-m+j}^T\ast v_c)}{{\sum }_{k=1}^{|V|}exp(u_k^T{v}_c)}\\ & =-\sum _{j=0,j\ne m}^{2m}{u}_{c-m+j}^T+2mlog\sum _{k=1}^{|V|}exp(u_k^T{v}_c)\end{array}$$

有了这个目标函数，我们就可以计算未知参数的梯度，并且在每次迭代中通过随机梯度下降来更新这些未知参数。

注意，
$$\begin{array}{rl}J& =-\sum _{j=0,j\ne m}^{2m}logP(u_{c-m+j}|v_c)\\ & =\sum _{j=0,j\ne m}^{2m}H(\hat{y},y_{c-m+j})\end{array}$$
其中，$H(\hat{y},y_{c-m+j})$是概率分布向量$\hat{y}$和独热向量$y_{c-m+j}$的交叉熵。

• 注释：在Skip-gram中只计算出了一个概率概率分布向量$\hat{y}$。Skip-gram对每个上下文词都一视同仁：该模型计算每个单词出现在上下文中的概率，且与它们(上下文词)和中心词的距离无关。

4.4 负采样(Negative Sampling)

让我们花点时间来看看目标函数。注意，在|V|上求和的代价是巨大的！我们所做的任何更新或对目标函数的评估都需要O(|V|)的时间复杂度，如果我们recall的话，需要数百万的时间。一个简单的想法是我们可以近似这个目标函数，也就是找其近似替代。

• CBOW和Skip-gram的损失函数J计算代价都很大，因为softmax，我们要将所有的|V|分数相加(也就是分母)。

对每一个训练步骤，我们不必在整个词汇表上循环，只需采样几个负例。我们从噪声分布$(P_n(w))$中“采样”，这个噪声分布的概率与词汇表的频率顺序相匹配。为了将我们对问题的表述扩大到包含负采样，我们需要做的就是更新：

• 目标函数
• 梯度
• 更新规则

Mikolov等人提出Negative Sampling in Distributed Representations of Words and Phrases and their Compositionality(在词和短语的分布表示及其构词性中呈现负抽样)。虽然负采样是基于Skip-gram模型的，但实际上它是在优化一个不同的目标。考虑一对中心词和上下文词对(c,w)。这词对来自训练数据集吗？让我们用P(D=1|w,c)来表示(c,w)来自语料库数据的概率。相应地，P(D=0|w,c)表示(c,w)不是来自语料库数据的概率。首先，我们用sigmoid函数来模拟(建模)P(D=1|w,c):
$$P(D=1|w,c,\theta )=\sigma (v_c^T\ast v_w)=\frac{1}{1+e^{(-v_c^T\ast v_w)}}$$

• sigmoid函数是softmax的1D版本，可用于模拟概率

现在，我们建立一个新的目标函数，在一个(上下文词,中心词)对确实在语料库数据中的情况下,这个函数会试图去最大化这个词对在语料库数据中的概率，如果这个词对实际不在语料库数据中的话，这个函数则会试图最大化这个词对不在语料库数据中的概率。

$$\begin{array}{rl}\theta & =\underset{\theta }{\mathrm{argmax}}\prod _{(w,c)\in D}P(D=1|w,c,\theta )\ast \prod _{(w,c)\in \tilde{D}}P(D=0|w,c,\theta )\\ & =\underset{\theta }{\mathrm{argmax}}\prod _{(w,c)\in D}P(D=1|w,c,\theta )\ast \prod _{(w,c)\in \tilde{D}}(1-P(D=1|w,c,\theta ))\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{(w,c)\in D}logP(D=1|w,c,\theta )+\sum _{(w,c)\in \tilde{D}}log(1-P(D=1|w,c,\theta ))\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{(w,c)\in D}log\frac{1}{1+exp(-u_w^T\ast v_c)}+\sum _{(w,c)\in \tilde{D}}log(1-\frac{1}{1+exp(-u_w^T\ast v_c)})\\ & =\underset{\theta }{\mathrm{argmax}}\sum _{(w,c)\in D}log\frac{1}{1+exp(-u_w^T\ast v_c)}+\sum _{(w,c)\in \tilde{D}}log(\frac{1}{1+exp(u_w^T\ast v_c)})\end{array}$$

注意，最大化似然与最小化负对数似然是相同的。

$$J=-\sum _{(w,c)\in D}log\frac{1}{1+exp(-u_w^T\ast v_c)}-\sum _{(w,c)\in \tilde{D}}log(\frac{1}{1+exp(u_w^T\ast v_c)})$$

注意$\tilde{D}$是一个“假”或者“负”("false"or “negative”)的语料库。在这个负语料库中我们会有如"stock boil fish is toy"这样的句子。不自然的句子(unnatural sentences)应该得到一个较低的发生概率。We can genarate $\tilde{D}$on the fly by randomly sampling this nagetive from the word bank(字库)。

对Skip-gram来说，我们给定中心词的观测上下文词$u_{c-m+j}$的新目标函数为：
$$-log\sigma (u_{c-m+j}^T\ast v_c)-\sum _{k=1}^{K}log\sigma (-\widetilde{u_k^T}\ast v_c)$$

对于CBOW来说，我们给定上下文词的观测中心词$u_c$的新目标函数为：
$$-log\sigma (u_c^T\ast \hat{v})-\sum _{k=1}^{K}log\sigma (-{\tilde{u}}_k^T\ast \hat{v})$$

在上述公式中，${\tilde{u}}_k|k=1...K$是从$P_n(w)$采样出的。让我们讨论一下$P_n(w)$应该是什么。虽然有很多关于什么是最佳近似(approximation)的讨论，但似乎一元模型(Unigram Model)的指数为$\frac{3}{4}$时的表现最好。为什么是$\frac{3}{4}$？下面是一个例子，这个例子可能有助于获得一些直觉：
$$\begin{gathered} is:0.9^{\frac{3}{4}}=0.92 \\ Constitution:0.09^{\frac{3}{4}}=0.16 \\ bombastic:0.01^{\frac{3}{4}}=0.032 \end{gathered}$$

"bombastic"的抽样率现在是原来的3倍，而"is"的抽样率只是略有上升。

• Skip-gram模型的常规softmax计算：
  $$-u_{c-m+j}^T\ast v_c+log\sum _{k=1}^{|V|}exp(u_k^T\ast v_c)$$
• CBOW模型的常规softmax计算：
  $$-u_c^T\ast \hat{v}+log\sum _{j=1}^{|V|}exp(u_j^T\ast \hat{y})$$

4.5 分层softmax(Hierarchical Softmax)

Mikolov等人同时也提出了分层softmax作为常规softmax的更有效替代。在实践中，分层softmax往往更适用于不频繁的词，而负采样则更适用于频繁词和低维向量。

分层softmax使用二叉树表示词汇表中的所有单词。树上的每一个叶子都是一个词，从根节点到叶都有一条唯一(unique)的路径。在这个模型中，没有单词的输出表示。相反，图的每个节点(出了根和叶)都与该模型要学习的向量相关联。

在这个模型中，给定向量$w_i$的单词w的概率，$P(w|w_i)$，等于从根节点到与单词w相对应的叶节点的随机游走的概率。这种方法计算概率的主要优点是计算成本仅为$O(log(|V|))$，对应于路径的长度。

• 分层softmax使用二叉树，其中叶子节点是词汇表中所有单词。一个单词作为输出单词(output word)的概率被定义为从根节点到该单词叶子的随机游走的概率。计算成本变成$O(log(|V|))$，而不是O(|V|)。
• 分层softmax的二叉树如下图所示：
  
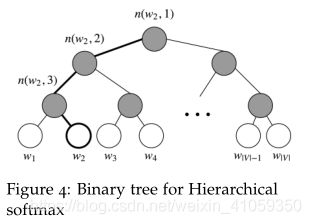
  我们来介绍一些符号(notation)。设$L(w)$为从根节点到叶节点w的路径中的节点数。例如，上图中的$L(w_2)$为3。设n(w,i)为此路径上的第i个节点与相关的向量$v_n(w,i)$。所以n(w,1)是根节点，而n(w,L(w))是w的父节点。现在对于每个内部节点n，我们任选它的一个子节点，并称为ch(n)(比如，始终是左节点)。然后我们可以将概率计算为：
  $$P(w|w_i)=\prod _{j=1}^{L(w)-1}\sigma ([n(w,j+1)=ch(n(w,j))]\ast v_{(w,j)}^T\ast v_{w_i})$$

$$其中，[x]=\{\begin{array}{l}1,ifxistrue\\ -1,otherwise\end{array},\sigma (.)为sigmoid函数$$

This formula is fairly dense,so let’s examine it more closely.

首先，我们根据从根节点(n(w,1))到叶节点(w)的路径的形状计算项的乘积。我们假设ch(n)总是n的左节点，那么当路径向左时，项$[n(w,j+1)=ch(n(w,j))]$返回1，如果路径向右，则返回-1。

此外，项$[n(w,j+1)=ch(n(w,j))]$提供规范化。在一个节点n，如果我们将到达左节点和右节点的概率相加，可以检查$v_n^T\ast v_{w_i}$的任何值都满足：
$$\sigma (v_n^T\ast v_{w_i})+\sigma (-v_n^T\ast v_{w_i})=1$$

这个规范化还可以确保${\sum }_{w=1}^{|V|}P(w|w_i)=1$，就像在原始的softmax中一样。

最后，我们使用输入向量$v_{w_i}$和内部节点向量$v_{n(w,j)}^T$的点积来比较这两个向量的相似性。让我们来看一个例子。取上图中的$w_2$，我们必须取两个左边，然后取一个右边，才能从根节点到达叶子节点$w_2$。所以：
$$\begin{array}{rl}P(w_2|w_i)& =p(n(w_2,1),left)\ast p(n(w_2,2),left)\ast p(n(w_2,3),right)\\ & =\sigma (v_{n(w_2,1)}\ast v_{w_i})\ast \sigma (v_{n(w_2,2)}\ast v_{w_i})\ast \sigma (-v_{n(w_2,1)}\ast v_{w_i})\end{array}$$

为了训练模型，我们的目标仍然是最小化负对数似然$-logP(w|w_i)$。但是，我们不更新每个词的输出向量，而是更新从根节点到叶节点(不包括根和叶)路径中的二叉树结点的向量。

这种方法的速度取决于二叉树的构造方式和单词分配给叶节点的方式。Mikolov等人使用二叉哈夫曼树(binary Huffman tree)，它在树种给频繁词分配较短的路径。

后记：终于在2019年的最后一天翻译完成了这个notes，回想去年跨年时立的flag，也是勉强完成了一些。今年继续努力，踏实走好每一步，同时也不要忘记拓宽视野，多参与好的活动。仰望星空，脚踏实地。加油~

---

Notes中的参考文献：

[Bengio et al., 2003] Bengio, Y ., Ducharme, R., Vincent, P ., and Janvin, C. (2003). A
neural probabilistic language model. J. Mach. Learn. Res., 3:1137–1155.

[Collobert et al., 2011] Collobert, R., Weston, J., Bottou, L., Karlen, M., Kavukcuoglu,
K., and Kuksa, P . P . (2011). Natural language processing (almost) from scratch.
CoRR, abs/1103.0398.

[Mikolov et al., 2013] Mikolov , T., Chen, K., Corrado, G., and Dean, J. (2013). Efficient
estimation of word representations in vector space. CoRR, abs/1301.3781.

[Rong, 2014] Rong, X. (2014). word2vec parameter learning explained. CoRR,
abs/1411.2738.

[Rumelhart et al., 1988] Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988).
Neurocomputing: Foundations of research. chapter Learning Representations by
Back-propagating Errors, pages 696–699. MIT Press, Cambridge, MA, USA.