【数据结构与算法】-＞算法-＞字符串匹配基础（中）-＞BM算法-＞KMP 三倍性能的强大算法

Ⅰ 前言

文本编辑器的查找替换功能相信大家都不陌生，很多 IDE 像 Eclipse，IntelliJ，包括 Word，都有这个功能，把一个词统一替换成另一个。那这个功能是如何实现的呢？

如果用前一篇文章里的 BF 算法和 RK 算法，当然可以实现这个功能，但是在某些极端情况下，BF 算法性能会退化得比较严重，而 RK 算法需要用到哈希算法，但是设计出一个可以应对各种类型字符的哈希算法并不简单。

对于工业级的软件开发来说，我们希望算法尽可能的高效，并且在极端情况下，性能也不要退化得太严重。那么，对于查找功能是重要功能的软件来说，比如一些文本编辑器，它们的查找功能都是用哪种算法来实现的呢？有没有比 BF 算法和 RK 算法更加高效的字符串匹配算法呢？

这就引出了我们这篇文章要讲的一个算法，BM（Boyer-Moore） 算法。它是一种非常高效的字符串匹配算法，有实验统计，它的性能是著名的 KMP 算法的 3 到 4 倍。BM 算法的原理很复杂，比较难懂，我会在王争老师的课程的基础，再加上我的理解，希望能把这个算法讲得更清楚一点。

如果对 BF 算法和 RK 算法还不熟悉的同学，如果有兴趣，可以跳转到下面的链接去看看。

【数据结构与算法】-＞算法-＞字符串匹配基础（上）-＞BF 算法 & RK 算法

Ⅱ BM 算法核心思想

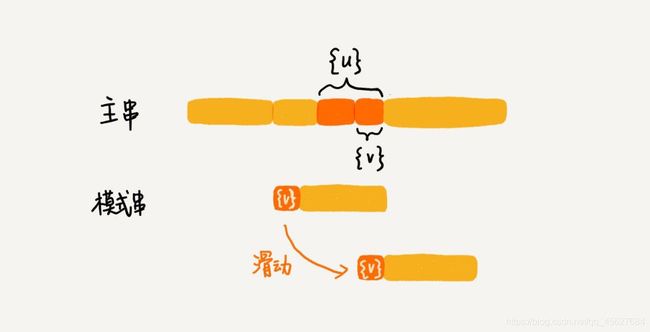
我们把模式串和主串的匹配过程，看作模式串在主串中不停地往后滑动。当遇到不匹配的字符时，BF 算法和 RK 算法的做法是，模式串往后滑动一位，然后从模式串的第一个字符开始重新匹配。如下面的这张图

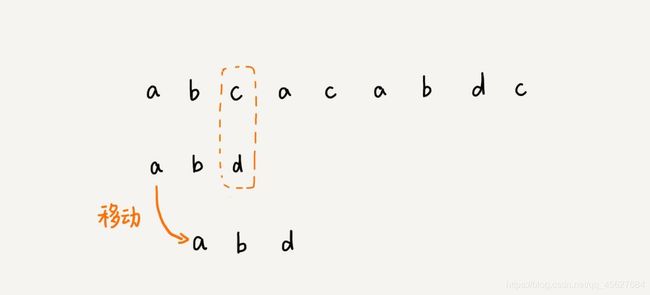
在这个例子里，主串中的 c ，在模式串中是不存在的，所以，模式串向后滑动的时候，只要 c 与模式串有重合，肯定无法匹配。所以，我们可以一次性把模式串往后多滑动几位，把模式串移动到 c 的后面。

所以，当遇到不匹配的字符时，有什么固定的规律，可以将模式串往后多滑动几位呢？这样移动地越快，匹配的效率就更高了。

BM 算法本质上其实就是在寻找这种规律。借助这种规律，在模式串与主串匹配的过程中，当模式串和主串某个字符不匹配的时候，能够跳过一些肯定不会匹配的情况，将模式串往后多滑动几位。

Ⅲ BM 算法原理分析

BM 算法包括两部分，分别是 坏字符规则（bad character rule） 和 好后缀规则（good suffix shift）。我们分别来看一看。

1. 坏字符规则

前面讲的 BF 算法和 RK 算法，在匹配的过程中，都是按照模式串的下标从小到大的顺序，依次与主串中的字符进行匹配的。这种匹配顺序比较符合我们的思维习惯，但是 BM 算法的匹配顺序很特别，它是按照模式串下标从大到小，倒着匹配的。

BF 算法

BM 算法

我们从模式串的末尾倒着匹配，当我们发现某个字符没法匹配的时候，我们把这个字符叫作 坏字符（主串中的字符）。

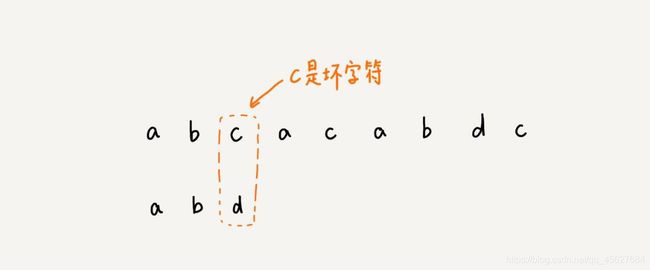
我们拿坏字符 c 在模式串中查找，发现模式串中并不存在这个字符，也就是说，字符 c 与模式串中的任何字符都不可能匹配。这个时候，我们可以将模式串直接往后滑动三位，将模式串滑动到 c 后面的位置，再从模式串的末尾字符开始比较。

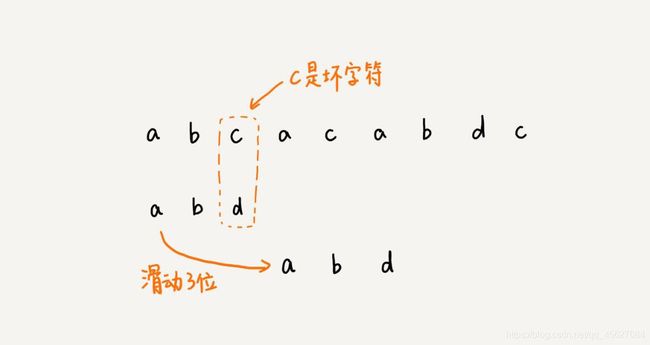
这个时候，我们发现，模式串中最后一个字符 d，还是无法和主串中的 a 匹配，这个时候，还能将模式串往后滑动三位吗？答案是不行的。因为这个时候，坏字符 a 在模式串中是存在的，模式串中下标是 0 的位置也是字符 a。这种情况下，我们可以将模式串往后滑动两位，让两个 a 上下对齐，然后再从模式串的末尾字符开始，重新匹配。

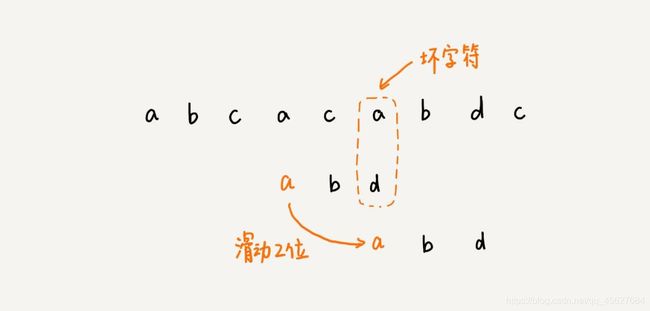
第一次匹配的时候，我们滑动了三位。第二次匹配的时候，我们滑动了两位。那具体滑动多少位，是不是可以总结出一个规律来？

当发生不匹配的时候，我们把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在，我们把这个坏字符在模式串中的下标记作 xi。如果不存在，我们把 xi 记作 -1。那么，模式串往后移动的位数就等于 si-xi。

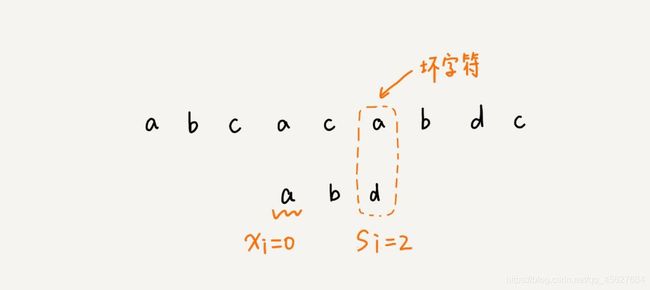
这里还有一点需要注意，就是如果坏字符在模式串里多次出现，那我们在计算 xi 的时候，选择最靠后的那个，因为这样就不会让模式串滑动过多，导致本来可能匹配的情况被滑动略过。

利用坏字符规则，BM 算法在最好情况下的时间复杂度非常低，是 O(n/m) 。比如，主串是 aaabaaabaaabaaab，模式串是 aaaa。每次比对，模式串都可以直接后移四位，所以，匹配具有类似特点的模式串和主串的时候，BM 算法非常高效。

不过，单纯使用坏字符规则还不够，因为 si - xi 计算出来的移动位数，有可能是负数，比如主串是 aaaaaaaaaaaaaa，模式串是 baaa。第一次比对， si 也就是坏字符对应的模式串中的字符下标，所以就是 0（b 是坏字符）；xi 就是坏字符在模式串中的下标，也就是 3（字符多次出现，取靠后的）。因而 si - xi = -3 。

利用坏字符规则，BM 算法在最好情况下时间复杂度非常低，是 O(n/m)。比如，主串是 aaabaaabaaabaaab，模式串是 aaaa。每次比对，模式串都可以直接后移四位，所以，匹配具有类似特点的的模式串和主串的时候，BM 算法非常高效。

不过，单纯使用坏字符规则还是不够的。因为根据 si - xi 计算出来的移动次数，有可能是负数，不但不会向后滑动模式串，还有可能倒退，所以，BM 算法还需要用到 “好后缀规则”。

2. 好后缀规则

好后缀规则实际上跟坏字符规则的思路很类似，比如下面这张图。当模式串滑动到图中的位置的时候，模式串和主串有 2 个字符是匹配的，倒数第 3 个字符发生了不匹配的情况。

这个时候该如何滑动字符串呢？当然，我们还可以利用坏字符规则来计算模式串的滑动位数，但是坏字符规则正如我们上面所说不是时时刻刻都有效的，所以我们还需要使用好后缀规则，两个配合使用。

我们把已经匹配好的 b c 叫作好后缀，记作 {u}。我们拿它在模式串中查找，如果找到了另一个跟 {u} 相匹配的子串 {u*}，那我们就将模式串滑动到子串 {u*} 与主串中 {u} 对齐的位置。

如果在模式串中找不到另一个等于 {u} 的子串，我们就直接将模式串滑动到主串中 {u} 的后面，因为之前的任何一次往后滑动，都没有匹配主串中 {u} 的情况。

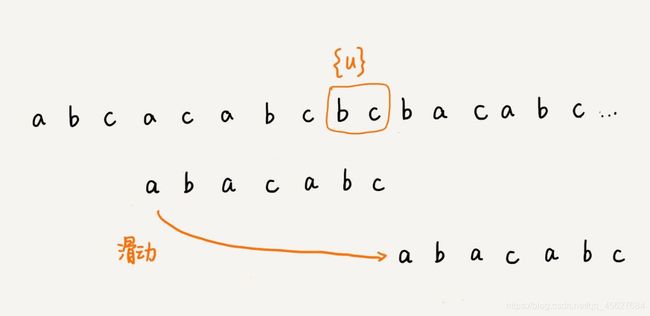
不过，当模式串中不存在等于 {u} 的子串的时候，我们直接将模式串滑动到主串 {u} 的后面，这样做会不会跳过头呢？我们看下面这种情况。这里面 b c 是好后缀，尽管在模式串中没有另外一个相匹配的子串 {u*}，但是如果我们将模式串移动到好后缀的后面，那就会错过模式串和主串可以匹配的情况。

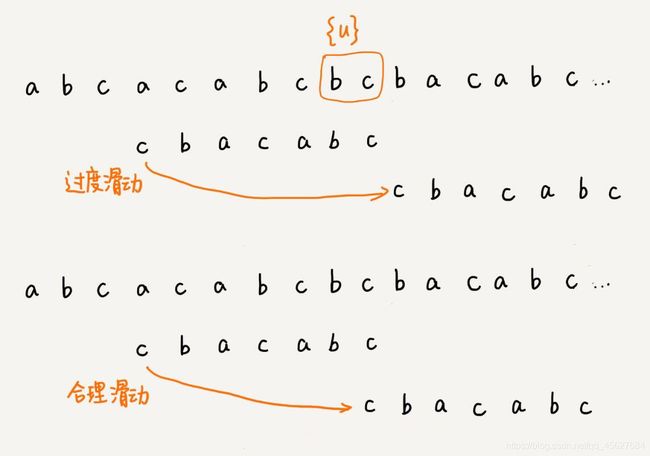
如果好后缀在模式串中不存在可匹配的子串，那在我们一步一步往后滑动模式串的过程中，只要主串中 {u} 与模式串有重合，那就肯定无法完全匹配。但是当模式串滑动到前缀与主串中的 {u} 的后缀有部分重合的时候，并且重合的部分相等的时候，就有可能会存在完全匹配的情况。

这个说起来比较复杂，大家看图可能就明白了。

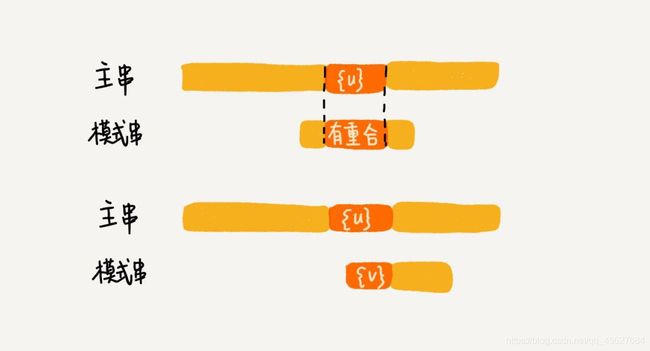
再进一步解释就是，在上一次配比的时候，已经发现了模式串中没有和主串好后缀可以匹配的子串，那模式串就要向后移动。这时候有个情况就是，模式串的中间的一部分和主串的好后缀重合了，那肯定是无法匹配的。因为模式串的头尾肯定和主串的子串不匹配，所以这种情况的重合就意义不大。

但什么情况下模式串的一部分和主串的后缀有重合才有意义呢？就是模式串的前缀子串和好后缀的后缀字串重合，这样如果后面也匹配的话，就是真的匹配了，就像我们上图举的合理滑动的例子。这个逻辑大家看看图仔细想想就可以想通了。

所以，针对这种情况，我们不仅要看好后缀在模式串中，是否有另一个匹配的子串，我们还要考察好后缀的后缀子串，是否存在跟模式串的前缀子串匹配的。

为了避免歧义，这里我再解释一下什么是前缀后缀子串。比如说有个字符串 s ，它的后缀子串就是最后一个字符和 s 对齐的子串。比如 abc 的后缀子串就是 c，bc。所谓前缀子串，就是起始字符和 s 对齐的子串，比如 abc 的前缀子串就是 a，ab。

我们要从好后缀的后缀子串中，找一个最长的并且能够跟模式串的前缀子串匹配的，假设是 {v}，然后将模式串滑动到如图所示的位置

这就是好后缀规则的基本原理。

那么模式串和主串中的某个字符不匹配的时候，如何选择用好后缀规则还是坏字符规则，来计算模式串往后滑动的位数呢？

我们前面说过，坏字符的移动位数可能会出现负数，除了这个情况意外，其他的移动都是安全的。这个安全就是指移动了以后，不会错过正确的字符串匹配。好后缀同样，也是安全的。所以在选择的时候，我们有一个处理原则，就是坏字符规则和好后缀规则的移动位数都进行一个计算，然后取两个数中最大的那个。因为按照我们最基本的思路，要使得每次出现不匹配字符时模式串移动的位数更大，这样查找起来就会更快。

因为好后缀规则不会出现移动位数是负数的情况，所以即使用坏字符规则算出来移动位数是负数，最后取得的移动位数也是正的，模式串会继续向后移动。

Ⅳ BM 算法代码实现

基础的思想和原理相信你看到这里已经明白了，现在我们就来实现 BM 算法。

我们一部分一部分来，先来实现坏字符规则。

1. 坏字符规则

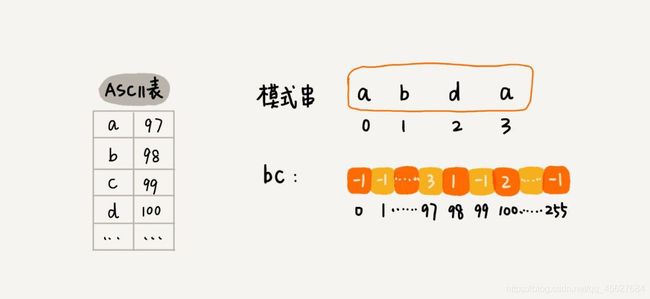
坏字符规则本身并不难理解，当遇到坏字符时，要计算往后移动的位数 si - xi，其中 xi 的计算是重点。那我们如何求得 xi ，也就是坏字符在模式串中出现的位置呢？

如果我们拿坏字符，在模式串中顺序遍历查找，这样就会比较低效，势必影响这个算法的性能。为了追求更高的效率，我们可以用散列表。

对散列表有疑惑的同学可以跳转去看我的这篇文章

【数据结构与算法】-＞数据结构-＞散列表（上）-＞散列表的思想&散列冲突的解决

我们可以将模式串中的每个字符及其下标都存到散列表中，这样就可以快速找到坏字符在模式串的位置下标了。

关于这个散列表，我们只实现一种最简单的情况，假设字符串的字符集不是很大，每个字符长度是 1 字节，我们用大小为 256 的数组，来记录每个字符在模式串中出现的位置。数组的下标对应字符的 ASCII 码值，数组中存储这个字符在模式串中出现的位置。

如果将上面的过程写成代码，就是下面这个样子

	private static final int SIZE = 256; //ASCII码数
	
	/**
	 * 借助散列表，存储字符以及其在模式串中的位置
	 * 如果是同样的字符出现多次，就记录它在模式串中最后出现的位置
	 * @param patternString 模式串
	 * @param badChar 坏字符集
	 */
	private void generateBadChar(char[] patternString, int[] badChar) {
     
		for (int i = 0; i < SIZE; i++) {
     
			badChar[i] = -1;	//初始化badChar数组
		}
		for (int i = 0; i < patternString.length; i++) {
     
			int ascii = (int) patternString[i];
			badChar[ascii] = i;  //记录模式串中同一个字符最后出现的位置
		}
	}

badChar就是上面说的散列表，我们要借助它快速找到坏字符在模式串中的位置。

这里我再解释一下第二个 for 循环，我们遍历模式串，然后在badChar中记录字符出现在模式串中的下标，大家可以看到，如果是同样一个字符第二次出现，就会把上一次记录的位置覆盖掉，这样最后就记录的是这个字符在模式串中最后出现的位置。这也是为了安全性考虑，如果记录的是前面出现的位置，那移动的位数就会很大，就会有错过正确字符串匹配的风险。大家仔细想想应该可以想明白。

掌握了坏规则之后，我们先把 BM 算法的框架写好，只完成坏字符规则的部分，先不考虑好后缀规则和坏字符规则 si - xi 计算得到的移动位数可能为负数的情况。代码如下

	/**
	 * BM算法实现字符串匹配
	 * @param mainString 主串
	 * @param patternString 模式串
	 * @return 模式串在主串中的位置
	 */
	public static int boyerMoore(char[] mainString, char[] patternString) {
     
		int[] badChar = new int[SIZE];
		generateBadChar(patternString, badChar); //构建坏字符哈希表
		
		int mainLength = mainString.length;
		int patternLength = patternString.length;
		
		int i = 0;
		while (i <= mainLength - patternLength) {
     
			int j;
			for (j = mainLength-1; j >= 0; j--) {
      //模式串从后向前匹配
				if (mainString[i+j] != patternString[j]) {
      //坏字符对应模式串中的下标位置为 j
					break;
				}
			}
			if (j < 0) {
     
				return i; //匹配成功，返回下标i
			}
			//等同于将模式串往后滑动 si-xi 也就是 (j - badChar[(int) mainString[i+j]])位
			i = i + (j - badChar[(int) mainString[i+j]]);
		}
		return -1;
	}

坏字符规则理解起来是容易点的，大家可以对着注释看看代码，应该就可以明白了。我再给出一张图，方便大家理解。

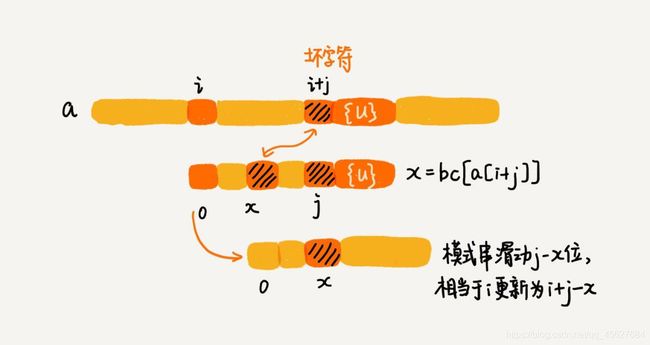
至此，我们已经实现了包含坏字符规则的 BM 算法，现在只需要再将好后缀规则填充进这个框架里。

2. 好后缀规则

根据上面的讲述，我们知道好后缀的处理规则中有两个最核心的内容：

1. 在模式串中，查找跟好后缀匹配的另一个子串；
2. 在好后缀的后缀子串中，查找最长的、能跟模式串前缀子串匹配的后缀子串。

我再来对这两条做一个解释。

我们前面讲好后缀规则的时候，说的第一种情况，就是模式串中有和好后缀可以配对的子串，这个其实很容易绕进去。我们先明确一个事情，就是好后缀意味了什么。能有好后缀，一定代表了配对的时候模式串的后缀子串和主串的一个子串重合了。就是下图中模式串最后两位的 b c 。

所以我们要再在模式串中找的可以和后缀子串配对的子串，是除了现在模式串中已经和主串的一个字串配对的后缀子串以外，要再找一个相同的子串。我们要找的是模式串中圈起来的这个 b c。

这就是第一条核心的意思，配合之前的图，大家再做一个理解。

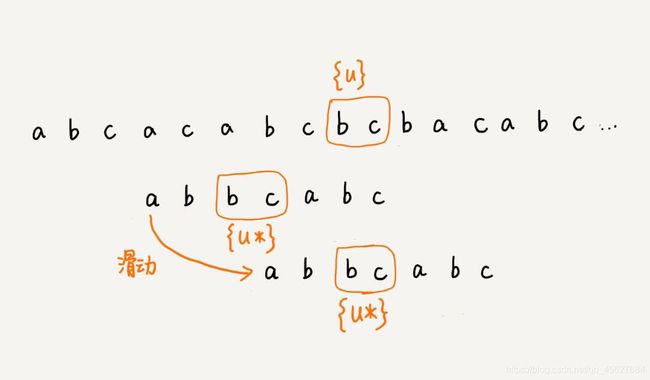
然后再来看第二条核心对应的另一种情况，就是我们要找前面的 b c ，但是模式串中已经没有了，那怎么办？这时候我们就找好后缀的后缀子串和模式串的前缀子串，有没有匹配的。找到的越长，能跳跃的就越多。

在不考虑效率的情况下，这两个操作可以用很“暴力”的匹配查找方式解决。但是，如果想要 BM 算法的效率很高，这部分就不能太低效。那我们要如何做呢？

因为好后缀也是模式串本身的后缀子串，所以，我们可以在模式串和主串正式匹配之前，通过预处理模式串，预先计算好模式串的每个后缀子串，对应的另一个可匹配子串的位置。这个预处理过程比较有技巧，很容易绕进去，是这篇文章中最难的一部分了。

我们先来看看，如何表示模式串中不同的后缀子串呢？因为后缀子串的最后一个字符的位置的固定的，下标为 m - 1，（m 为模式串的长度），所以我们只需要记录长度就可以了。通过长度，我们可以确定出唯一的后缀子串。

现在我们要引入最关键的变量 suffix 数组 。这个数组是用来存放后缀子串的。suffix 数组的下标 k 表示后缀子串的长度为 k，下标对应的数组值存储的是，在模式串中跟好后缀 {u} 相匹配的子串 {u*} 的起始下标值。

这就对应着我们前面说的第一个核心。我用一个例子来做个说明。

再强调一下，我们在模式串中找的是和后缀子串相配的子串，不是找模式串的后缀子串的位置。前面我们已经说过了，既然有后缀子串，就说明后几位已经配对上了，所以找的是其他位置的子串，因为我们是要通过这个位置来往后移动，使得模式串中的这个子串走到和好后缀相对应的地方。所以上图中的 suffix[4] 和 suffix[5] 都是 -1，因为除了已经和好后缀配对的后缀子串外，模式串里已经没有另一个可以配对的子串了。

那么，如果模式串中有多个（大于 1 个）子串跟后缀子串 {u} 匹配，那 suffix 数组中该存储哪个子串的起始位置呢？为了避免模式串往后滑动得过头了，我们肯定要存储模式串中最靠后的那个子串的起始位置，也就是下标最大的那个子串的起始位置。这和我们的坏字符的处理是一样的，还记得吗？都是为了防止滑动过大，所以出现了同样的字符或字符串，都取靠后的那个。

		for (int i = 0; i < patternString.length; i++) {
     
			int ascii = (int) patternString[i];
			badChar[ascii] = i;  //记录模式串中同一个字符最后出现的位置
		}

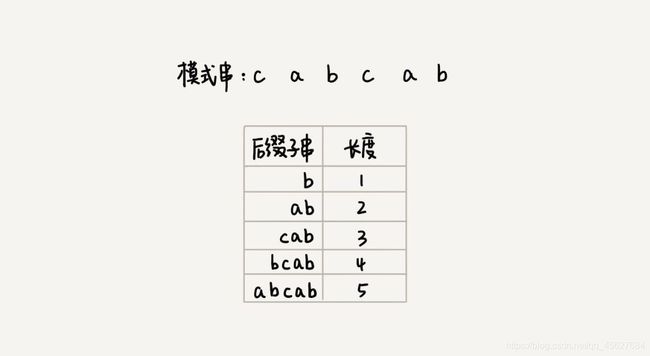
如果这么说还不够清晰的话，我再举个例子。比如我们有一个模式串如下

这个就比上面多了个 a b ，我还是和上面一样做个简单的分析

后缀子串	长度	Suffix
b	1	suffix[1] = 4
ab	2	suffix[2] = 3
cab	3	suffix[3] = 0

那我们这样处理就足够了吗？如果有多个子串和后缀子串 {u} 匹配的话。

实际上，仅仅是选最靠后的字串片段来存储是不够的。我们再次回忆一下好后缀规则。

我们不仅要在模式串中，查找跟好后缀匹配的另一个子串，还要在好后缀的后缀子串中，查找最长的能跟模式串前缀子串匹配的后缀子串。

其实对应的还是这张图。我们在前面说过，如果是模式串的一个子串和好后缀重合，那一定不是匹配的，只有当模式串的前缀子串和好后缀的后缀子串重合，才有可能匹配。

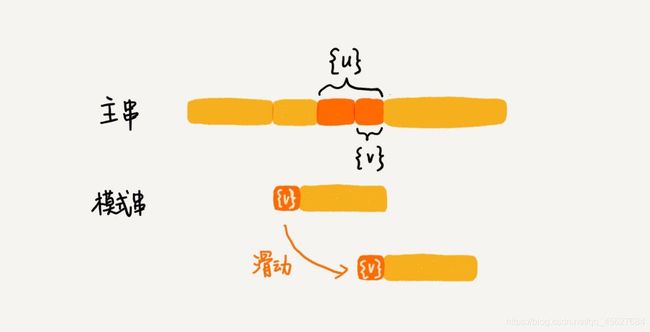
我们如果只记录刚刚定义的 suffix，实际上，只能处理规则的前半部分，也就是在模式串中，查找跟好后缀匹配的另一个子串。所以，除了 suffix 数组之外，我们还需要一个 boolean 类型的 prefix 数组，来记录模式串的后缀子串是否能匹配模式串的前缀子串。

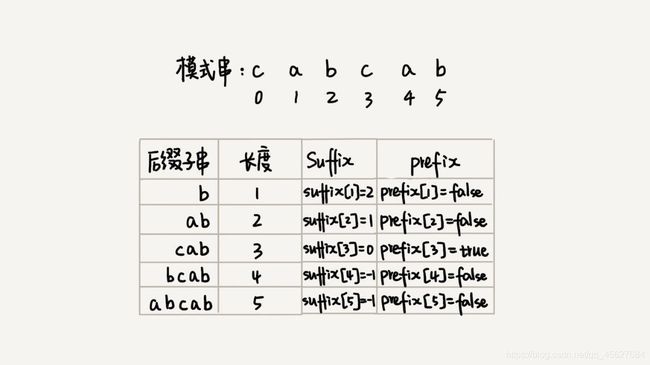
看了前面的讲解，我相信你已经理解了为什么只有 prefix[3] = true，像后缀字符串是 ab，这时候 ab 虽然有可以配对的子串，就是下标为 1 开始的那个 ab，但是模式串的前缀子串是 ca，和 ab 不匹配，就为 false。因而只有 prefix[3] = true 。

现在，我们就来看看如何计算并填充这两个数组的值，这个计算过程也非常巧妙。

我们拿下标从 0 到 i 的子串（i 可以是 0 到 m-2）与整个模式串，求公共后缀子串。如果公共后缀子串的长度是 k，那我们就记录 suffix[k] = j（j 表示公共后缀子串的起始下标）。如果 j == 0，也就是说，公共后缀子串也是模式串的前缀子串，我们就记录 prefix[k] = true。

这个逻辑是什么意思呢？我再进一步地讲解一下。

我们现在的目的是要求能跟模式串后缀子串匹配的前缀子串，如果整个模式串的长度为 m，那么模式串的下标就是 [0, m-1]，这个我相信大家都理解。那么，模式串的最大前缀子串就是 [0, m-2]，所以 i 的取值范围就是 0 到 m-2 。

比如我们把 i = 2 时的子串拿出来，和整个模式串求公共后缀子串，这样求出来的就和上面我们的例子中一样，为了便于说明，我再用上面的例子画个图。

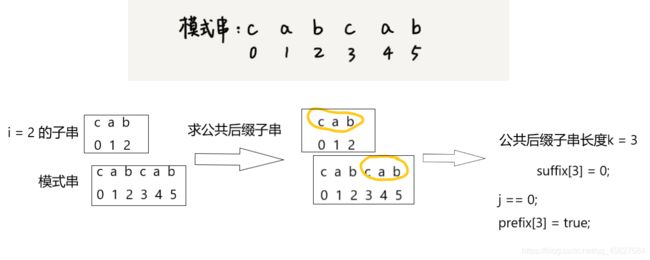
现在我们把 suffix 数组和 prefix 数组的计算过程，用代码实现，大家可以做一个对照。

	/**
	 * 初始化 suffix、prefix数组
	 * @param patternString 模式串
	 * @param suffix
	 * @param prefix
	 */
	private static void generateGoodSuffix(char[] patternString, 
											int[] suffix, boolean[] prefix) {
     
		int patternLength = patternString.length;
		
		for (int i = 0; i < patternLength; i++) {
      
			suffix[i] = -1;
			prefix[i] = false;
		}
		for (int i = 0; i < patternLength-1; i++) {
      //取出一个[0, i]的子串和模式串找公共后缀子串
			int j = i;
			int k = 0;
			while (j >= 0 && patternString[j] == patternString[patternLength-1-k]) {
     
				j--;
				k++;
				suffix[k] = j + 1;
			}
			if (j == -1) {
      //表示公共后缀子串也是模式串的前缀子串
				prefix[k] = true;
			}
		}
	}

同样的，如果大家对这段代码觉得有些混乱的话，可以对着代码做一遍变量跟踪，再结合着我的解析，相信应该还是可以理解的。

有了这两个数组之后，我们现在来看，模式串跟主串匹配的过程中，遇到不能匹配的字符时，如何根据好后缀规则，计算模式串往后滑动的位数。

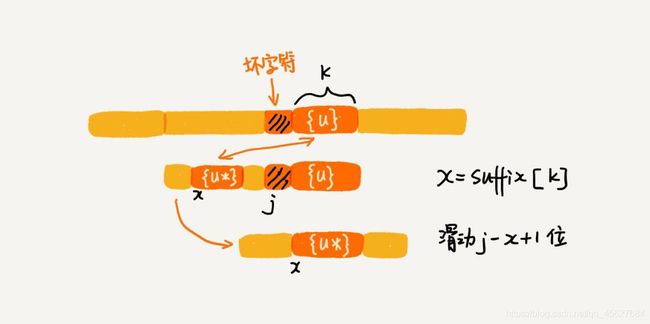
假设好后缀的长度是 k 。我们先拿好后缀，在 suffix 数组中查找其匹配的子串。如果 suffix[k] 不等于 -1 （-1 表示不存在匹配的子串），那我们就将模式串往后移动 j - suffix[k] + 1 位 （j 表示坏字符对应的模式串中的字符下标）。

如果 suffix[k] 等于 -1，表示模式串中不存在另一个跟好后缀匹配的子串片段。我们可以用下面这条规则来处理。

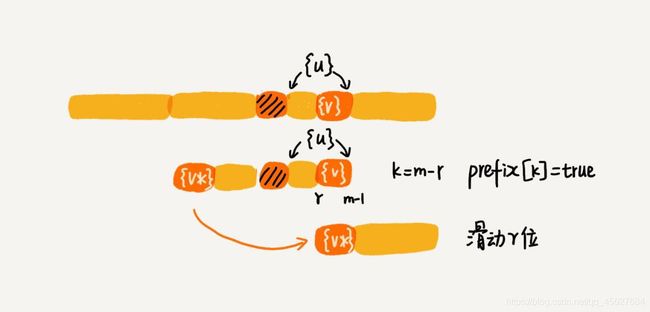
好后缀的后缀子串 b[r, m-1]（其中，r 取值从 j+2 到 m-1）的长度 k = m-r，如果 prefix[k] 等于 true，表示长度为 k 的后缀子串，有可匹配的前缀子串，这样我们可以把模式串后移 r 位。

关于 r 的取值，我这里要再多说一句。当时我学的时候觉得就很迷惑，这个取值是怎么来的，好半会都没反应过来。在前面我们说，j 是坏字符对应的模式串中的字符下标，也就是说，在 j 的下一个字符，就是好后缀了。那我们要求好后缀的后缀子串，就要再往后走一格，因为后缀子串是包含第一个字符的，不然就不是后缀了，所以 r 的取值是从 j+2 开始的。

这个情况就对应了我们前面讲的，需要找和好后缀的后缀子串配对的模式串中的最大前缀子串。我们需要将这个前缀子串后移到和好后缀的后缀子串对应的位置上。如下图所示

如果这两条规则都没有找到可以匹配好后缀或者其后缀子串的子串，就说明这是我们讲的好后缀的第一种情况，可以直接向后移动整个模式串的位数。

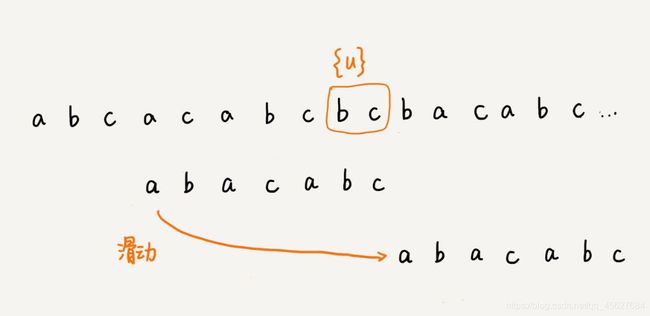
至此，好后缀规则的代码思路我们也理清了，可以直接把好后缀规则的代码加到前面我们写的 BM 算法的框架中去，这样就得到了 BM 算法的完整实现。

3. 代码完整实现

package com.tyz.string_matching.core;

/**
 * 用BM算法实现字符串匹配
 * @author Tong
 */
public class BoyerMoore {
     
	private static final int SIZE = 256; //ASCII码数

	public BoyerMoore() {
     }
	
	/**
	 * 借助散列表，存储字符以及其在模式串中的位置
	 * 如果是同样的字符出现多次，就记录它在模式串中最后出现的位置
	 * @param patternString 模式串
	 * @param badChar 坏字符集
	 */
	private static void generateBadChar(char[] patternString, int[] badChar) {
     
		for (int i = 0; i < SIZE; i++) {
     
			badChar[i] = -1;	//初始化badChar数组
		}
		for (int i = 0; i < patternString.length; i++) {
     
			int ascii = (int) patternString[i];
			badChar[ascii] = i;  //记录模式串中同一个字符最后出现的位置
		}
	}
	
	/**
	 * 初始化 suffix、prefix数组
	 * @param patternString 模式串
	 * @param suffix
	 * @param prefix
	 */
	private static void generateGoodSuffix(char[] patternString, 
											int[] suffix, boolean[] prefix) {
     
		int patternLength = patternString.length;
		
		for (int i = 0; i < patternLength; i++) {
      
			suffix[i] = -1;
			prefix[i] = false;
		}
		for (int i = 0; i < patternLength-1; i++) {
      //取出一个[0, i]的子串和模式串找公共后缀子串
			int j = i;
			int k = 0;
			while (j >= 0 && patternString[j] == patternString[patternLength-1-k]) {
     
				j--;
				k++;
				suffix[k] = j + 1;
			}
			if (j == -1) {
      //表示公共后缀子串也是模式串的前缀子串
				prefix[k] = true;
			}
		}
	}
	
	/**
	 * 用好后缀规则计算模式串移动位数
	 * @param j 坏字符对应的模式串中的字符下标
	 * @param patternLength 模式串长度
	 * @param suffix
	 * @param prefix
	 * @return 好后缀规则计算出的移动位数
	 */
	private static int moveByGoodString(int j, int patternLength, 
									int[] suffix, boolean[] prefix) {
     
		int k = patternLength - 1 - j; //好后缀长度
		if (suffix[k] != -1) {
     
			return j - suffix[k] + 1; //模式串里有和好后缀相配的子串
		}
		for (int r = j+2; r <= patternLength-1; r++) {
     
			if (prefix[patternLength-r] == true) {
     
				return r; //模式串有可以和好后缀的后缀子串相配的前缀子串
			}
		}
		return patternLength; //模式串里只有后缀子串和好后缀相配
	}
	
	/**
	 * BM算法实现字符串匹配
	 * @param mainString 主串
	 * @param patternString 模式串
	 * @return 模式串在主串中的位置
	 */
	public static int boyerMoore(char[] mainString, char[] patternString) {
     
		int[] badChar = new int[SIZE];
		generateBadChar(patternString, badChar); //构建坏字符哈希表
		
		int mainLength = mainString.length;
		int patternLength = patternString.length;
		
		int[] suffix = new int[patternLength];
		boolean[] prefix = new boolean[patternLength];
		generateGoodSuffix(patternString, suffix, prefix);
		
		int i = 0;
		while (i <= mainLength - patternLength) {
     
			int j;
			for (j = patternLength-1; j >= 0; j--) {
      //模式串从后向前匹配
				if (mainString[i+j] != patternString[j]) {
      //坏字符对应模式串中的下标位置为 j
					break;
				}
			}
			if (j < 0) {
     
				return i; //匹配成功，返回下标i
			}
			int x = j - badChar[(int) mainString[i+j]];
			int y = 0;
			if (j < patternLength-1) {
      //坏字符不在最后一位，说明存在好后缀
				y = moveByGoodString(j, patternLength, suffix, prefix);
			}
			//将模式串向后移动好后缀规则和坏字符规则计算出的移动位数最大的那个
			i = i + Math.max(x, y);
		}
		return -1;
	}

}

我觉得我的注释已经写得很详细了，大家可以结合我的注释以及前面的讲解，来理解这里的代码。

Ⅴ BM 算法的性能分析及优化

我们先来分析 BM 算法的内存消耗。整个算法用到了额外的三个数组，其中 badChar数组的大小跟字符集大小有关，suffix数组和 prefix数组的大小跟模式串长度 m 有关。

如果我们处理字符集很大的字符串匹配问题，badChar数组对内存的消耗会比较多。因为好后缀和坏字符规则是独立的，如果我们对运行的环境对内存要求严苛，可以只是用好后缀规则，不使用坏字符规则，这样就可以避免 badChar数组过多的内存消耗。不过，单纯地使用好后缀规则，BM 算法的效率就会下降一些了。

实际上，我们讲的这个 BM 算法是个初级版本，基于这个初级的版本，在极端情况下，预处理计算 suffix 数组、prefix 数组的性能会比较差。

比如模式串是 aaaaaaa 这种包含很多重复的字符的模式串，预处理的时间复杂度就是 O(m²)。当然，大部分情况下，时间复杂度不会这么差。

BM 算法的时间复杂度分析起来非常复杂，这篇论文 “A new proof of the linearity of the Boyer-Moore string searching algorithm” 证明了在最坏情况下，BM 算法的比较次数上限是 5n。这篇论文“Tight bounds on the complexity of the Boyer-Moore string matching algorithm” 证明了在最坏情况下，BM 算法的比较次数上限是 3n。

若对 KMP 算法有兴趣的同学，可以继续看我的下一篇文章
【数据结构与算法】-＞算法-＞字符串匹配基础（下）-＞KMP 算法

另，这篇文章的主要内容来源于极客时间王争的《数据结构与算法之美》