字符串匹配基础（下）：如何借助BM算法轻松理解KMP算法？

------ 本文是学习算法的笔记，《数据结构与算法之美》，极客时间的课程 ------

上一节我们讲了BM算法，尽管它很复杂，也不好理解，但却是工程中非常常用的的一种高效字符串匹配算法。有统计说，它是最高效，最常用的字符串匹配算法。不过，在所有字符串匹配算法里，要说最知名的一种的话，那就非KMP算法莫属。很多时候，提到字符串匹配，我们首先想到的就是KMP算法。

尽管在实际开发中，我们几乎不大可能自己新手实现一个KMP算法。但是，学习这个算法的思想，作为你开拓眼界，锻炼下逻辑思维，也是极好的。

KMP算法的基本原理

KMP算法是根据三位作者（D.E.Knuth，J.H.Morris和V.R.Pratt）的名字全名的，算法的全称是Knuth Morris Pratt算法。

KMP算法的核心思想，跟上一节讲的BM算法非常相近。我们假设主串是 a，模式串是 b。要模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，我们希望找到一些规律，可以将模式串往后多滑动几位，跳过那些肯定不会匹配的情况。

还记得我们上一节讲到的好后缀和坏字符吗？这里我们可以类比一下，在模式串和主串匹配的过程中，把不能匹配的那个字符仍然叫作坏字符，把已经匹配的那段字符串叫作好前缀。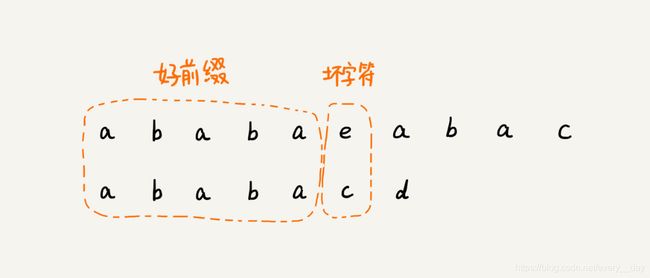

当遇到坏字符的时候，我们就要把模式串往后滑动，在滑动的过程中，只要模式串和好前缀有上下重合，前面几个字符的比较，就相当于拿好前缀的后缀子串，跟模式串的前缀子串在比较。这个比较的过程能否更高效了呢？可以不用一个字符一个字符地比较了吗？

KMP算法就 是在试图寻找一种规律：在模式串和主串匹配的过程中，当遇到坏字符后，对于已经比对过的好前缀，能否找到一种规律，将模式串一次性滑动很多位？

我们只需要要拿好前缀本身，在它的后缀子串中，查找最长的那个可以跟好前缀子串匹配的。假设最长的可匹配的那部分前缀子串是{v}，长度是k。我们把模式串一次性往后滑动 j-k 位，相当于每次遇到坏字符的时候，我们就把 j 更新为 k，i 不变，然后继续比较。

为了表述方便，我把好前缀的所有后缀子串中，最长的可匹配前缀子串的那个后缀子串，叫做最长可匹配后缀子串；对应的前缀子串，叫作最长可匹配前缀子串。

如何来求好前缀的最长可匹配前缀和后缀子串呢？这个只涉及模式串本身，可提前构建一个数组，用来存储模式串中每个前缀（这些前缀有可能是好前缀）的最长可匹配前缀子串的尾字符的下标。我们把它定义为next数组。也叫作失效函数（failure function）数组的下标是每个前缀尾字符的下标，数组的值是这个前缀的最长可匹配前缀子串的结尾字符下标。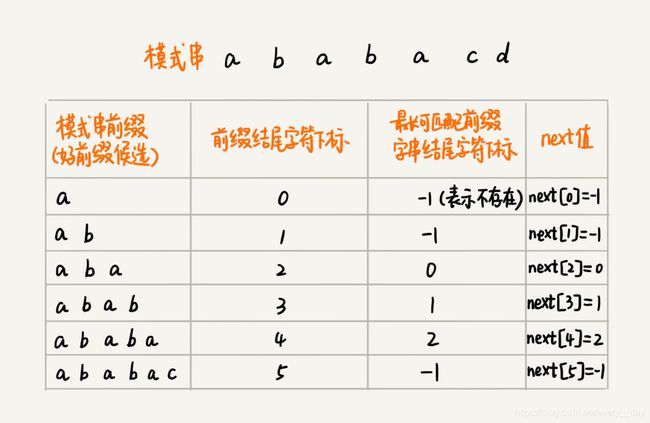

有了next数组，我们很容易就可以实现KMP算法了。我先假设 next数组已经计算好了，先给出 KMP 算法的框架代码。

失效函数计算方法

KMP算法的基本原理就讲完了，我们现在来看最复杂的部分，也就是next数组如何计算出来？

当然，我们可以用非常笨的方法，比如要计算这个模式串 b 的next[4]，我们就把 b[0,4]所有后缀子串，从长到短找出来，依次看看，是否能跟模式串的前缀子串匹配。很显然，这个方法也可以计算得到next数组，但是效率非常低。有没有更加高效的方法呢？

这里的处理技巧，类似于动态规划。不过动态规则我们在后面才会讲，这里换种方法来解释。

我们按照下标从小到大，依次计算next数组的值。当我们要计算 next[i] 时候，前面的 next[0]， next[1]， next[2]，…， next[n]应该已经计算出来了。利用已经计算出来的next值，我们是否可以快速推导出next[i]的值呢？

如果 next[i-1] = k-1,也就是说，子串 b[0,k-1]是b[0,i-1]的最长可匹配前缀子串。如果子串b[0,k-1] 下一个字符 b[k]，与 b[0,i-1]的下一个字符 b[i] 匹配，那子串 b[0,k] 就是 b[0,i] 的最长可匹配子串。所以 next[i] = k。但是，如果 b[0,k-1] 的下一个字符 b[k] 跟 b[0,i-1] 的下一个字符 b[i] 不相等呢？

我们假设 b[0,i] 的最长可匹配后缀子串是 b[r,i]。如果我们把最后一个字符去掉，那 b[r,i-1]肯定是 b[0,i-1] 的可匹配后缀子串，但不一定是最长的可匹配后缀子串。所以，既然 b[0,i-1] 最长可匹配后缀子串对应的模式串的前缀子串的下一个字符并不等于 b[i]，那我们就可以考察 b[0,i-1] 的次长可匹配后缀子串（也就是next[k]） b[x,i-1] 对应的可匹配前缀子串 b[0, i-1-x] 的下一个字符 b[i-x] 是否等于 b[i]。如果等于，那 b[x,i] 就是 b[0,1] 的最长可匹配后缀子串.。如果不相等，重复上面的过程。结合这张图，还有代码，来说说怎么求next的值

		// b表示模式串，m指模式串的长度
		private int[] getNexts(char[] b, int m) {
			int[] next = new int[m];
			next[0] = -1;
			int k = -1;
			for(int i = 1; i < m; ++i) {
				while( k != -1 && b[k+1] != b[i]) {
					k = next[k];
				}
				if(b[k+1] == b[i]) {
					++k;
				}
				next[i] = k;
			}
			return next;
		}

next[0] = -1, next[1] = -1 这两个很好理解。

求next[2] ，需要比较两个下标值是否相等（next[1]+1=0，即比较下标0和2，是否相等。相等则next[2]=next[1]+1）得next[2] = 0;

求next[3] ，需要比较两个下标值是否相等（next[2]+1=1，即比较下标1和3，是否相等。相等则next[3]=next[2]+1）得next[3] = 1;

求next[4] ，需要比较两个下标值是否相等（next[3]+1=2，即比较下标2和4，是否相等。相等则next[4]=next[3]+1）得next[4] = 2;

求next[5] ，需要比较两个下标值是否相等
（next[4]+1=3，即比较下标3和5，是否相等。不相等，进入循环，
先求出next[next[4]] +1 = next[2] + 1 = 1， next[4]这个说明ababa 的最长可匹配前缀子串 是 aba，次长子串是a,相当于当模式串为aba时，它的最长可匹配前缀子串，即next[2],即比较下标1和5，是否相等。不相等继续循环。
先求出next[next[next[4]]] +1 =0，即比较下标0和5，不相等。
循环结束，因为已经比到首个元素了，已经到头了。所以 next[5] = -1）

这里说明一下，循环结束的条件就是 特定的两个下标对应的值相等，或者没有可比的了。

KMP算法复杂度分析

空间复杂度很容易分析，KMP算法只需要额外的 next数组，数组的大小跟模式串相同。所以空间复杂度是O(m)，m表示模式串的长度。

KMP算法包含两部分，第一部分是构建next数组，第二部分才是借助 next 数组匹配。所以，关于时间复杂度，我们要分别从这两部分来分析。

先说第一部分，计算 next 数组的代码中，外层 for循环，执行m-1次，内层while循环，它的平均执行次数不怎么好统计，假设为k，那时间复杂度是O(k*m)。这个不好分析，我们换种方法

我可以找一些参照变量，i 和 k。i 从1开始一直增加到m，而 k 并不是每次for 循环都会增加，所以，k 累积增加的值肯定小于m。而while 循环里的 k=next[k]，实际上是在减小 k 的值，k 累积都没有增加超过m，所以 while 循环里面 k=next[k] 总的执行次数可不可能超过 m。因此， next 数组计算的时间复杂度是O(m)。

第二部分，i 从0 循环增长到 n-1，j的增长量不可能超过 i，所以肯定小于 n。而while循环中的那长语句 j=next[j-1]+1，不会让 j 增长的，那有没有可能让 j 不变呢？可没有可能。因为next[j-1] 的值肯定小于 j-1，所以 while 循环中的这条语句实际上也是让 j 的值减少。而 j 总共增长的量都不会超过 n，那减少的量也不可能超过 n，所以 while 循环中的这条语句总的执行次数也不会超过 n，所以这部分的时间复杂度是O(n)。

所以，综合两部分的时间复杂度，KMP算法的时间复杂度是O(m+n)。