巨大数的简单运算

一：背景

        当前计算机对于数据的处理是存在一定限度的，用与计算处理各种数据，c语言提供了许多整数类型，一般情况系使用int类型即可，但是要满足特定任务和机器要求的时候，数据超出处理范围时就需要使用另外的方法对这些数据进行处理，虽然float类型（可表示的数据范围是 ）和double类型（可表示的数据范围- ）也可以使用，但是float的有效位数只有7位，double类型的有效位数也只有15位，处理数据不够精确，数据的位数越多，丢失的信息量也越大。因此我们提供一种对位数超出表示范围的数据的处理工具——也就是这个巨大数的处理工具。

---

二：核心技术

1：万进制

万进制的原理同二进制十进制是一样的，二进制是逢二进一，同理万进制就是逢万进一。

优点：1、将巨大数当作字符串处理时，会使用字符型数组来存储它，也就是说将巨大数中的每一位数字视作一个字符存储进数组，每个字节存储一个数字字符；若是使用一万进制的话，每次将存储四个字节，数组中的每个元素取值为0~9999，和使用字符串的效率相同。

2、之所以使用万进制，而不用更高的进制位，是因为在涉及乘法的计算中依然要是数据保持在int类型可以表示的范围之内（例：若使用十万进制，当出现99999×99999 = 9999800001，但是很明显9999800001已经超出了int类型的表示范围，因此一万进制是最合适的进位）。在进行加法运算时，对应位置进行加和之后都会有进位的可能，为保证所有数据都不遗失，设置进位的问题：在本位出存储的数据是该数字本身对10000取余的结果，再进位处存储该数字本身对10000取整的结果。

       例如：15789—>存储在本位的是 5789，存储在进位的是 0001；

2：自定义补码

在巨大数处理过程中，为了避免对负数操作过程中引起的复杂运算，引用到自定义补码，与反码的原理相似（反码表示法规定：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外）而对于自定义补码，则是将负数的每一位与9取反，同样符号位是除外的。

自定义补码用于巨大数的加法和减法运算。

---

三：巨大数存储的结构体

typedef struct HUGE_NUMBER {
	char symbol;	//存储从文件中读取到的巨大数的符号
	int *data;		//存储巨大数的数字部分
	int dataCount;	//存储巨大数数字部分数组元素的个数
	int power;		//存储小数权重
} HUGE_NUMBER;

特别注意，dataCount = （数字的个数 + 3 ） /  4。例如154 2673 8265，dataCount  = （11 + 3）/ 4 = 3。

---

四：四则运算

1、加法

加法分为有进位和无进位两种情况，有进位又有一种特殊情况：进位饱和。

我们一步一步分析：

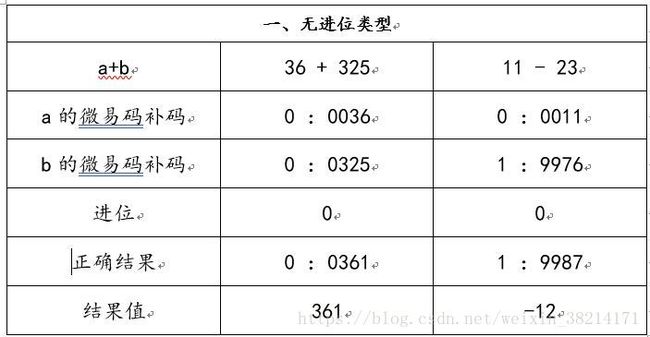
先看无进位情况：

无进位类型是最普通的情况，在此也就不赘述了。但是，有一个问题，结果的符号怎么确定呢？1表示负数，0表示正数。那么结果的符号就是用两个数的符号和进位异或运算。例如：36+25=361。结果的符号 = 0 ^ 0 ^ 0 = 0。

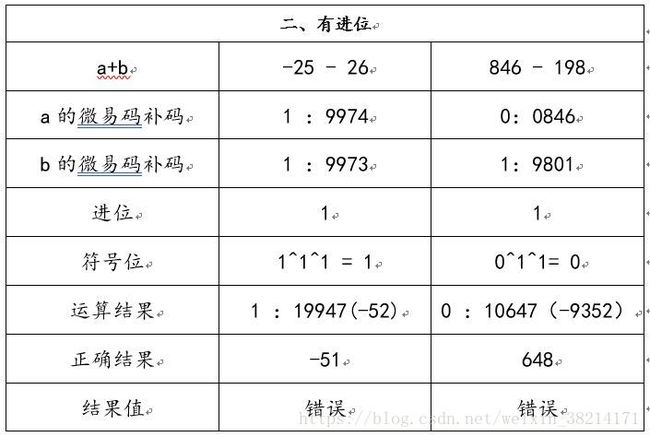
再看有进位情况：

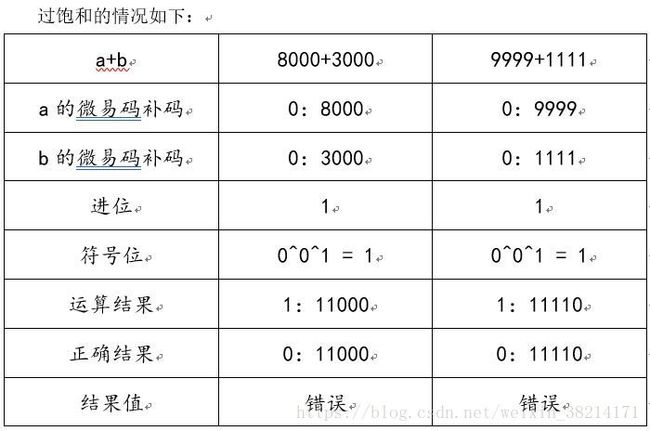
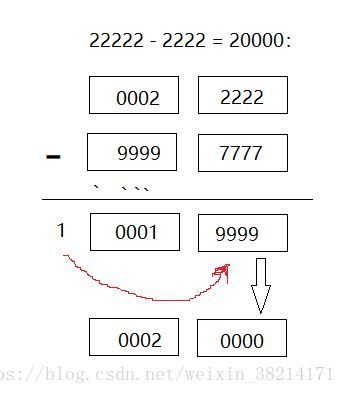
请注意，在有进位情况下，运算的结果和正确结果相差1。所以，在有进位的情况下，将进位数加到最后的运算结果上，即对9947再加上进位就是9948，转换过后就是-51。 这种手法运用到无进位的情况下，即最后的结果加上进位0，也是正确的。但是，这种情况有一个大问题，比如8000+3000=11000，把进位加到最后的运算结果上，则结果反而变成了1001，而且最后结果的符号经过和进位异或运算也是错误的。所以，为解决这种情况，我们需要给原本的数据前多加一个辅助位，即正数前面补上0000，负数前面补上9999。如果在有辅助位的情况下，还存在进位，则需要把最后的进位加到前面的数据上，如10000-9999和22222-2222。

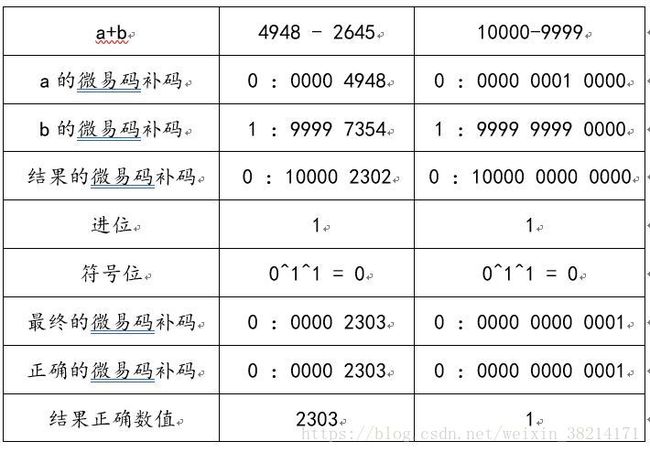
正确的如下：

在这种进位饱和的情况下，我们需要将最后的进位加到前面的数据上。

如果最后结果的符号是0，即正数，直接取得。如果符号是1，即负数，需要再对这个负数取一次微译码补码，才能得到正确的结果。 

//巨大数的加法：分为有进位和无进位两种情况，有进位存在进位饱和的状况。
//为解决进位饱和，就要将它视作无进位，实现这种方式的方法就是在原本数据的前面加上辅助位(故result长度多1个)：正数前面补上0000，负数前面补上9999。 
//假设（num1长度为2，num2长度为1）,例10000和9999。 
//申请一个存储加法结果result的空间，result的长度是num1和num2最大长度加1（考虑到进位），即3；
//第一个循环（实现相加和连续进位）：当巨大数长度和result的长度不相等时， 给巨大数前面补0。 
//result的长度比num1和num2的最大长度还大1。 
//result的符号是num1，num2，进位三者异或运算得来
//第二个循环：若第一个循环出现进位饱和的情况下，第二个循环才起作用。 
void addHugeNumber(HUGE_NUMBER *num1, HUGE_NUMBER *num2, HUGE_NUMBER *result) {
	int carry = 0;
	int i;
	int eachResult;
	
	result->dataCount = (num1->dataCount > num2->dataCount ? num1->dataCount : num2->dataCount) + 1;
	result->data = (int *) calloc(sizeof(int), result->dataCount);
	
	for(i = 0; i < result->dataCount; i++) {
		if(i >= num1->dataCount) {
			num1->data[i] = 0;
		} 
		if(i >= num2->dataCount) {
			num2->data[i] = 0;
		} 
		eachResult = getMecCode(num1->data[i], num1->symbol) + getMecCode(num2->data[i], num2->symbol) + carry;
		result->data[i] = eachResult % 10000;
		carry = eachResult / 10000;
	}
	result->symbol = num1->symbol ^ num2->symbol ^ carry;
	for(i = 0; i < result->dataCount; i++) {
		eachResult = result->data[i] + carry;
		result->data[i] = getMecCode(eachResult % 10000, result->symbol);
		carry = eachResult / 10000;
	}
}

//微译码补码：（与反码原理相似） 
//若为正数，补码与源码相等。
//若为负数，将负数的每一位与9取反（符号位除外）。 
int getMecCode(int data, char symbol) {
	return ((symbol == MINUS) ? (9999 - data) : data);
}

---

2、减法

减法运算是在加法的基础上进行的，在进行减法时，把其中一个数变为它的相反数，再调用加法函数即可。

void subHugeNumber(HUGE_NUMBER *num1, HUGE_NUMBER *num2, HUGE_NUMBER *result) {
	opposite(num2);
	addHugeNumber(num1, num2, result);
}

//实现减法借位很麻烦，干脆求第二个数相反数，调用加法函数即可。 
void opposite(HUGE_NUMBER *num) {
	if(num->symbol == POSITIVE) {
		num->symbol = MINUS;
	} else {
		num->symbol = POSITIVE;
	}
}

---

3、乘法

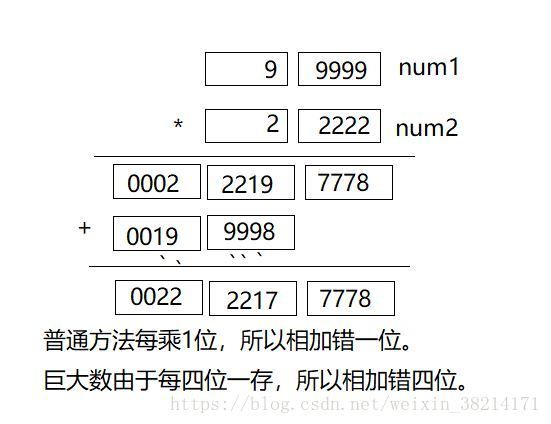
一般的乘法过程：

巨大数的乘法过程：

for(i = 0; i < num2->dataCount; i++) {
		carry = 0;
		resIndex = i;
		for(j = 0; j < num1->dataCount; j++) {
			eachResult = num1->data[j] * num2->data[i] + carry;
			carry = (eachResult + result->data[resIndex]) / 10000;
			result->data[resIndex] = (eachResult + result->data[resIndex]) % 10000;
			resIndex++;
		}
		result->data[resIndex] = carry;
	}

代码过程分析：

五：总结

通过巨大数这个项目的练习，加深了我对C语言函数调用，指针方面的理解。老师说C语言是考验程序员基本功语言，也是考验程序员素质的语言。如果大量的malloc，calloc申请空间，却不进行free释放，会产生严重的内存泄漏。 但是在Java语言中，free的过程就由jvm自己执行了，我们就不需要考虑，释放的过程。所以，在C编程中，一定一定记得申请空间，完了就要释放空间。

用自定义补码的方式来实现加法，确实是让人眼前一亮的处理方法。让我想到了计算机中补码存在的意义，我想，计算机中补码存在的原因，可能其中之一就是为了利用加法实现减法吧。

学习一定要找到自己的方法，千万不能看别人。一定要做最高效的学习，如果实在学不进去，就干脆彻底放松一下，恢复好了再投入学习。一定不能迷迷糊糊的学，这样既没有效率，也浪费时间。当人们处在最困难，最艰难，最崩溃的边缘，大多数人选择的是放弃，只有少部分人能真正的坚持下来，笑到最后。要想真正的坚持下来，不仅要有好的心态，更要对自己的学习进行总结，找到最有效率的学习方法。一旦熬过了这个最艰难的时刻，一定会柳暗花明。