数据结构与算法-----9.散列表：

1.概念：散列表，又称为哈希表。

2.散列思想：散列表使用的是数组支持利用下标随机访问数据的特性，散列表是数组的一种扩展，由数组演化而来，可以说：没有   数组就没有散列表。

3.为什么需要使用散列表这种数据结构：

因为当我们存储结构简单的数据时，可以存入数组中，然后通过下标索引来快速查找。但是如果存储的是例如：zhansan----10,lisi----20,这种一一映射的对应关系时，就不能直接存储在数组中，但是可以对数组稍加修改，通过某种方法，将对应关系中的一类数据转化成数组的下标，然后将另一类数据当成元素来存储。所以就变成这种key---value的结构。下标就是key，元素就是value。所以这种将key转化为数组下标的方法就叫做Hash函数（或散列函数）。

哈希表的查找效率之所以高效，就是因为它利用了数据根据下标随机访问元素的时间复杂度为O(1)这种特性。

4.散列函数：

散列函数在散列表中起着非常重要的作用，散列函数设计的好，那么可以降低哈希冲突的概率，也就提高了hash表的性能。

散列函数设计的基本要求：

（1）因为数据下标是从0开始的，所以通过散列函数计算出的值，一定是一个非负数。

（2）如果key1 == key2，那么hash(key1) == hash(key2)。

（3）如果key1 != key2，那么hash(1) != hash(key2)。（理想状态下）

但是第三点是不可能实现的，如果实现了，那么就不可能出现Hash冲突了。之所以出现了hash冲突，就是因为key值不同，但是计算出来的hash值相同了。

5.散列冲突问题及解决：

散列冲突问题无法避免，通常解决该问题的方法有两种：(1)开放寻址法，(2)链表法。

开放寻址法核心思想：如果发生了散列冲突，就重新探测一个空闲位置，将元素插入。

1）线性探测法：（插入元素操作）跟据hash函数计算出当前元素在散列表中的对应位置后，如果当前位置为空，那么存储元素。如果不为空，那么认为发生hash冲突，需要从当前位置顺序遍历散列表，直到找到空闲位置为止。

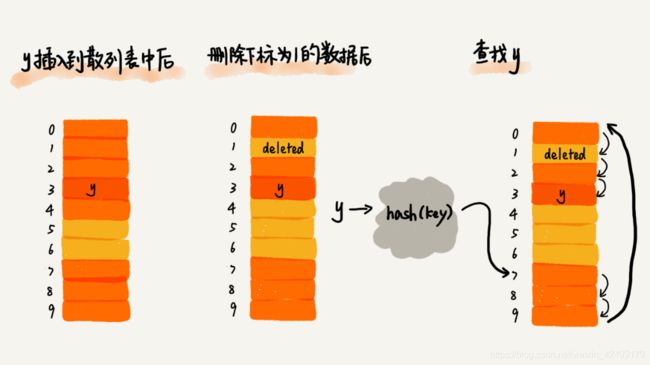
（查找元素操作）跟插入操作类似，根据hash函数定位数据下标，判断下标对应的key是否与要查找的key相等，相等返回，如果不相等，那么从当前位置顺序向后查找，如果遇到空闲位置还没有找到，那么就认为当前哈希表中没有当前元素。

所以会有一个问题发生，当我们从哈希表中删除一个元素之后，这时候再次查询，有可能出现需要查找的元素刚好在被删除元素的后面，那么就会出现找不到的情况。所以解决该问题的方法是：在哈希表中删除一个元素之后，需要做一个标记，比如标记为delete，那么当碰到这个标记时，可以继续查找。

如果采用线性探测法解决哈希冲突问题，当哈希表中的数据越来越多时，空闲的位置越来越少，那么发生冲突的概率就会越来越大，最坏的情况下从O(1)退变成为O(n)。

除了线性探测法之外，还有另外两种探测方法：二次探测法，双重散列法。

二次探测法：线性探测为每次移动一位，0，1，2，3.......，二次探测是每次移动的步数为原来的二次方，0，1^2,2^2,3^2......

双重散列法：如果第一次计算出的散列值发生冲突，那么就用第二个散列函数计算，直到找到空闲位置。

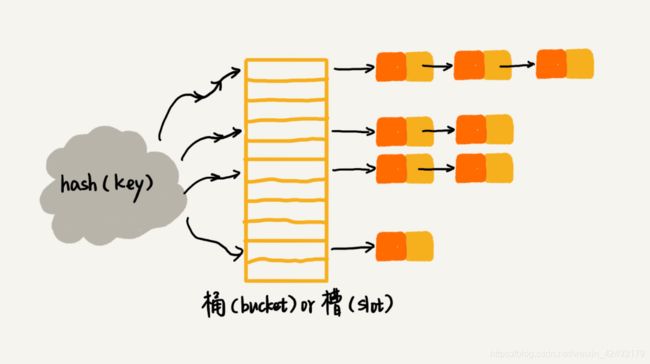
6.链表法解决hash冲突：

链表法是更加常用的解决hash冲突的方法，在散列表中的每个槽后面，都有一个链表，对于散列值相同的元素，都会以链表的形式存放。使用链表法解决hash冲突，插入操作，时间复杂度为O(1)，查找和删除操作的时间复杂度与链表的长度有关。

如何选择解决哈希冲突的方法：

开放寻址法：（优点）它是将散列表中所有的数据都存放在数组中，可以充分利用CPU的缓存来提高查询效率。（缺点）因为数据全部放在数组中，所以冲突的代价更高。所以当数据量小,扩容因子小的时候，适合使用该方法。Java中的ThreadLocalMap中就是使用该方法。

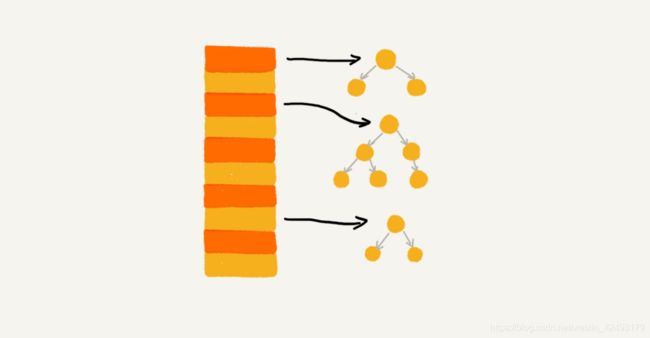
链表法：（缺点）由于链表需要额外存储指针，所以需要占用额外的空间。链表在内存中的地址是不连续的，所以不能充分利用CPU缓存的特性来加速查询。（优点）如果存储的是大对象，那么指针对应的内存占用可以忽略不记，链表法对于内存的使用率比较高，而且当生成的链表比较长的时候，可以将链表变体称为红黑树等数据结构，加快查询的效率。

所以基于链表解决冲突的散列表适合解决承装大对象，数据量大的情景。

7.尽量防止发生哈希冲突的方法：

（1）无论采取什么方法，当哈希表中的空闲位置太少时，都会增加哈希冲突的概率，所以为了尽量防止哈希冲突，那么需要对哈希表进行扩容，增加空闲位置的数量，什么时候扩容需要一个界限，这个界限就是扩容因子。

扩容因子 = 添入散列表中元素的数量 / 散列表的长度

扩容因子越大，空闲位置越少，冲突越多，性能越低。

（2）将散列函数尽可能设计的合理，因为如果散列函数设计的不合理，那么会增加哈希冲突的概率，从而降低了散列表的查询效率。

极端情况下，如果对数据进行精心的设计，每个数据经过散列函数得到的散列值都一样，那么它们就会每次落入同一个槽中，如果我们采用链表的形式解决哈希冲突，那么散列表就会退化称为链表，查询效率从O(1)变成O(n)。如果散列表中有10万条数据，退化后的查询效率就降低了10万倍。如果之前查询一条数据耗时0.1s，那么现在就是10000s，可能导致系统无法响应，从而达到DOS(拒绝服务攻击)的目的。

8.如何合理的设计散列函数和对散列表进行动态的扩容：

设计散列函数的基本要求：（1）不能太复杂，因为太复杂需要计算的时间更长。（2）通过散列函数计算出来的散列值要尽可能的随机，并且均匀分布，这样即使发生了哈希冲突，也能够均匀的落在每一个槽中，避免单一链表过长。

动态扩容：当扩容因子达到一定的界限时，就会触发动态扩容机制，默认扩大为原来的两倍。

动态扩容的原理是：重新申请两倍大小的新空间，然后将散列表中的数据搬移到新的散列表中。所以在散列表中插入一个数据，最好情况下，直接插入即可，为O(1)，最坏情况下，需要启动扩容操作，时间复杂度为O(n)，通过均摊法，平均时间复杂度还是O(1)。

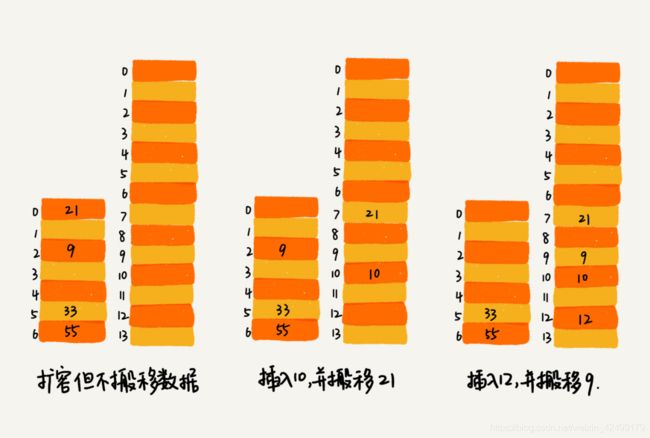
如何避免扩容的低效性：如果散列表中的数据大小有1GB，当发生扩容操作时，将旧的散列表中的数据搬移到新的散列表中，需要耗费相当长的时间。避免低效扩容的做法是：扩容的时候先不全部搬移数据，每次插入一个新数据的时候，从旧的散列表中搬移一个数据到新的散列表中，当有查询操作的时候，先从旧的散列函数中查询，如果查询不到，再从新的散列表中查询。这样就避免了一次搬移全部数据消耗大量的时间。

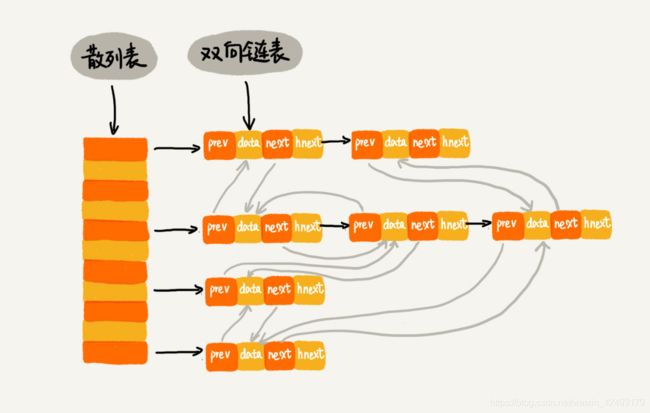
9.为什么好多数据结构都是将散列表和链表组合在一起使用：

例如LRU缓存功能：如果简单的使用单向链表来实现，那么它的查找的时间复杂度为O(n)，如果通过散列表+双向链表的方式来实现LRU，那么在查找的时候，通过散列表O(1)，然后再通过双向链表来进行插入和删除操作，所以无论查询，插入，删除，都是O(1)。