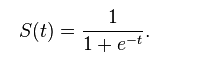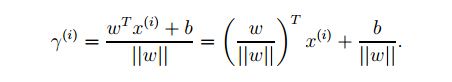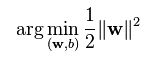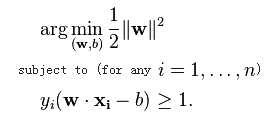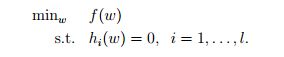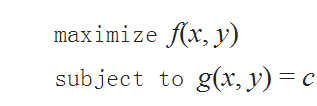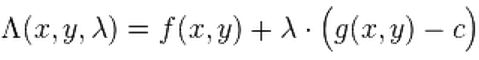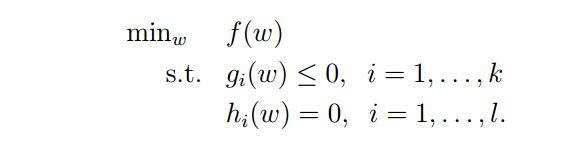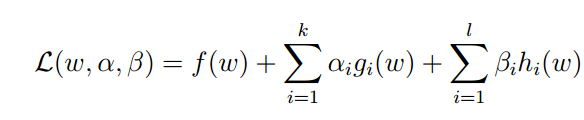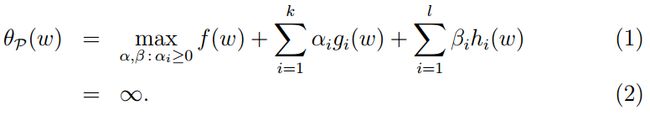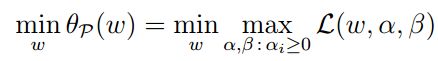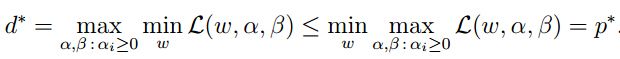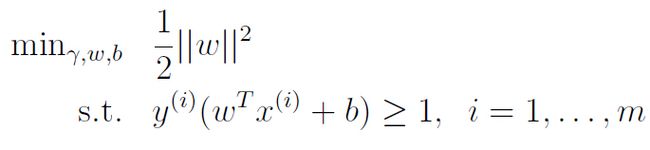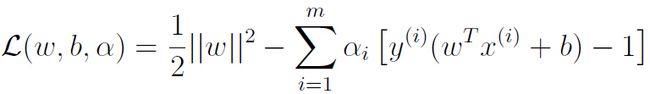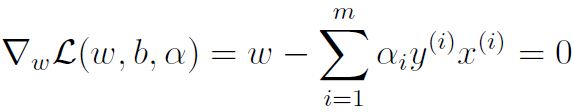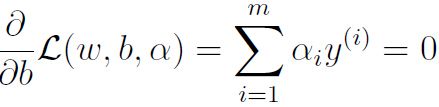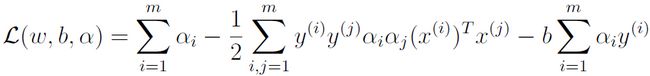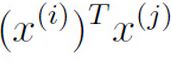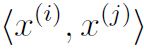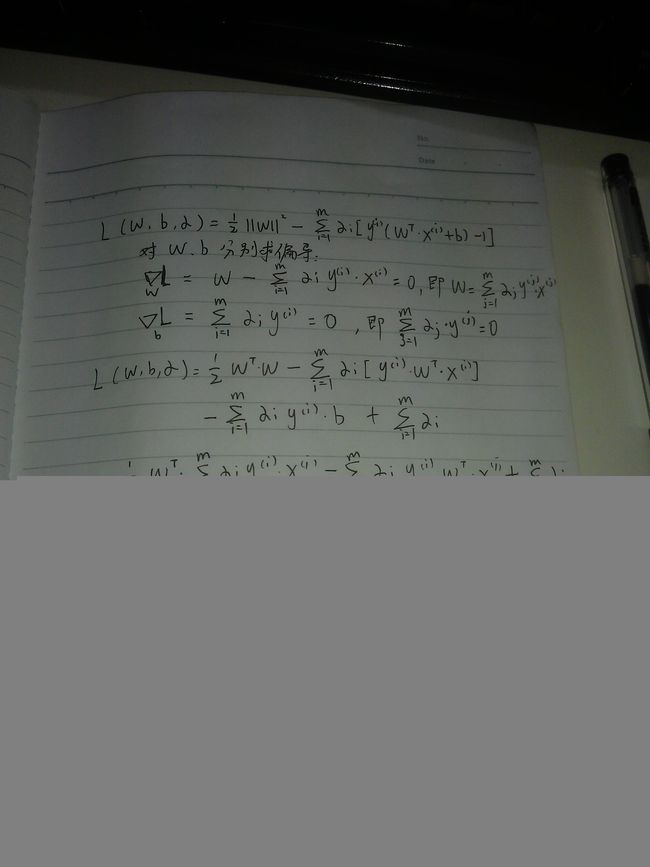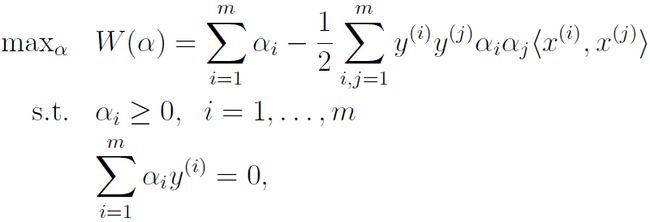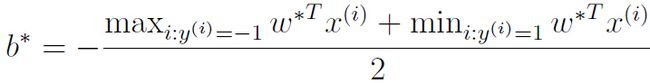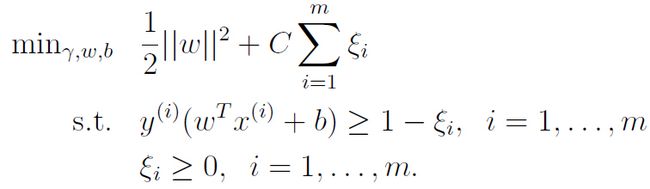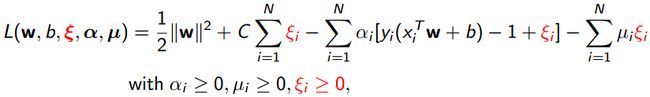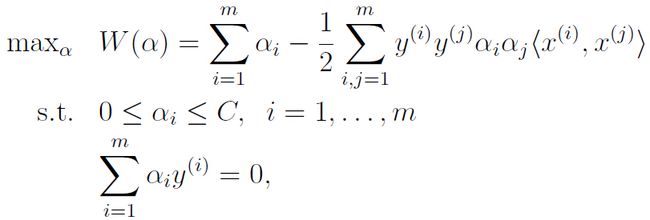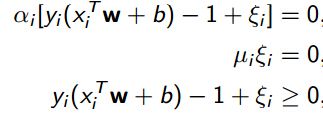svm学习理解笔记

最近一直在看machinelearning in action这本书，学习到很多知识，目前花费时间最多的是在Classification里面的svm（Support vector machines），主要原因是里面涉及到的数学相关的知识之前没有接触过，故本文边补习数学知识边学习svm.

1 svm简介

svm（支持向量机）主要就是在一个高维或者无限维中构造一个hyperplane（超平面），通过这个hyperplane将数据分割开来，从而达到分类目的。

a support vector machine constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks（http://en.wikipedia.org/wiki/Support_vector_machine）

2 什么是hyperplane？

t

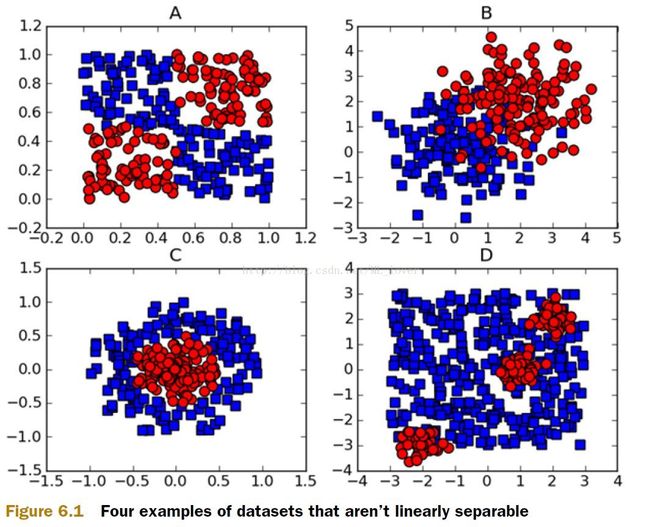
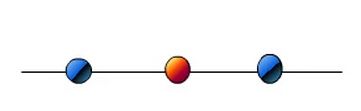
图6.1上的ABCD中的数据，能否用一条直线将颜色不同的数据区分出来呢？

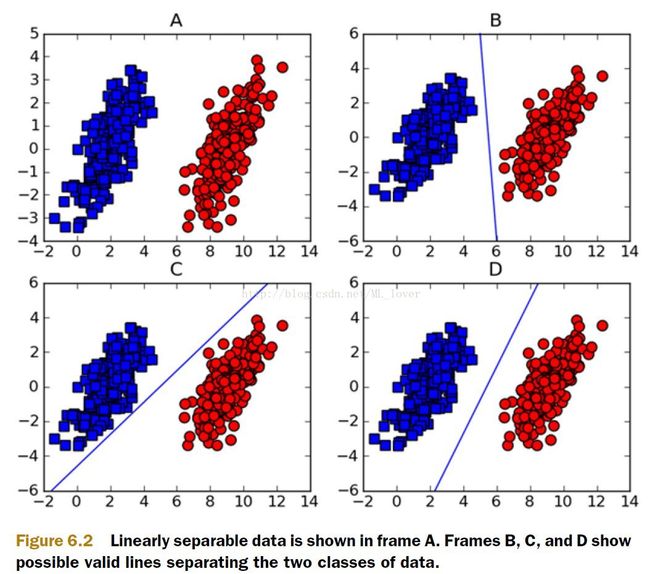
那图6.2上的ABCD中的数据呢？

很明显图6.2中的数据是可以用直线来将不同类型的数据划分开来，存在这样的一中解决方案，就说，这些数据是linearly separable（线性可分），同时这条用来分割图上的数据集的直线就被称为separating hyperplane（分离超平面），在2维上，separating hyperplane就是个直线(y=kx+b)，如果我们的数据集是3D的，那么用来划分3D数据的就是个平面，如果我们的数据是1024D的话，我们需要一个1023D的东西来划分目标数据，那这个1023D的东西是什么呢？或者说1023D这个对象该怎么称呼它呢，在抽象到N维上呢？我们就把这一个N-1D的对象称呼为hyperplane，hyperplane就是我们的decision boundary（判断边界），理想情况下，同一个边界范围内的数据是属于同一类对象的（实践情况下总有一些特殊的数据会跑到另外一个边界去了，后面在谈）。

3 什么是margin？

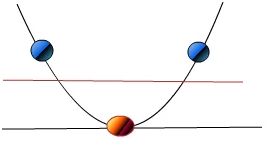
从图6.2上B、C、D上来看，这些hyperplane都可以将数据分开，那么哪一个是我们真正需要的？也就是说哪一个是最优的?对于我们来说，We’d like to make our classifier in such a way that the farther a data point is from the decision boundary, the more confident we are about the prediction we’ve made。

对于图6.2的B和C来说，BC上点到面的平均距离似乎比D的要少，按照平均距离这中方法去寻找最佳直线是否可行呢？按照平均距离来说是可行的，但是这并不是最好的主意。

 We’d like to find the point closest to the separating hyperplane and make sure this is as far away from the separating line as possible. This is known as margin （我们需要找到每类中距离分离超平面最近的点，同时确保这些点远离这个超平面，越远越好，这就是所谓的margin）

PS：在http://en.wikipedia.org/wiki/Support_vector_machine上，margin是这样定义的

we can select two hyperplanes in a way that they separate the data and there are no points between them, and then try to maximize their distance. The region bounded by them is called "the margin"

Maximum-margin hyperplane and margins for an SVM trained with samples from two classes. Samples on the margin are called the support vectors.

4 什么是support vector

在0x03中末尾的那些点，就是所谓的support vector（按照wiki上的定义就是margin上的点就是support vectors）。

5 目标

现在要做的就是找到一个hyperplane，使得support vectors距离hyperplane最大。

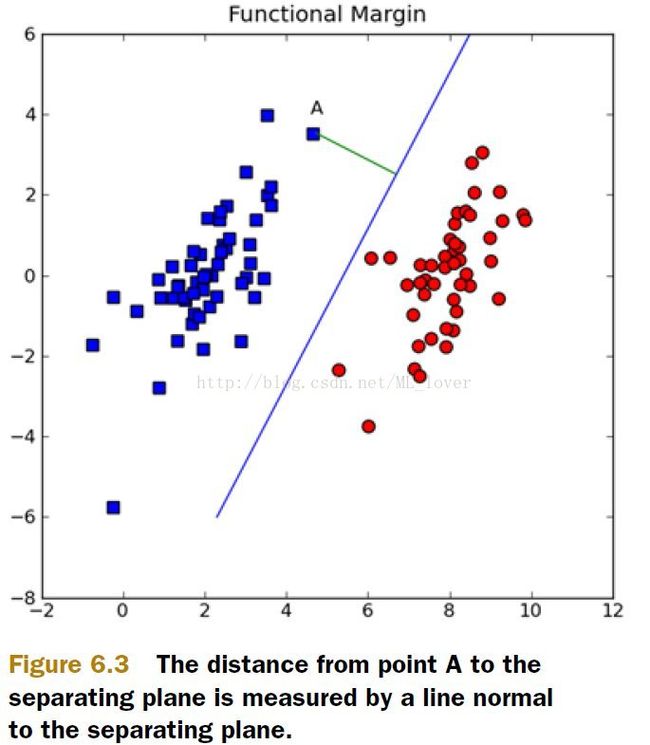
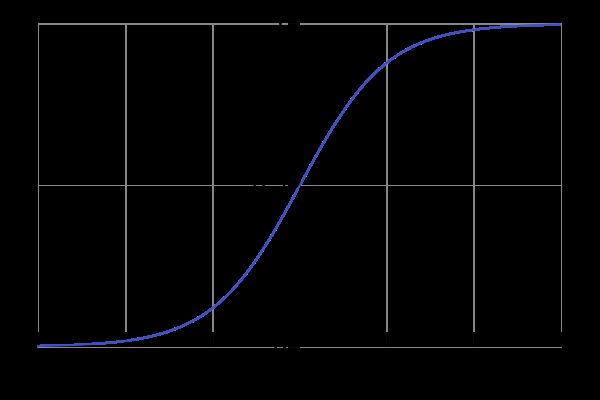
看图6.3，超平面可以用W’X+b来表示，W、X都是vector，如果我们要确定A到线的垂直距离，可以用|W‘X+b| /||W||来表示。

b就像是一个截距，比如一元线性方程y=kx+b中的b，W和b全部一起描述了这个hyperplane（线）

6 sigmoid函数

定义：

图像：

（http://en.wikipedia.org/wiki/Sigmoid_function）

PS:第一次听到和见到sigmoid函数是Ng在视频中提到的:)

从sigmoid函数可以看到这个函数的特性，在定义区间内，当x=0的时候，y=0.5，当x大于0后，y迅速区域1，当x小于0时，y迅速趋于0。鉴于这种特性，可以定义一个类似sigmoid的函数f（W‘X+b），这样f(x)当x<0的时候，f(x)取-1，反之取1，sigmoid的值是0和1，为什么要用class labels的值-1和1去代替0和1呢？Why did we switch from class labels of 0 and 1 to -1 and 1? This makes the math manageable, because -1 and 1 are only different by the sign.（主要原因是为了从数学计算方便考虑的，符号上的0、1、-1并不影响真正的分类）

Y*f（W’X+b），这里Y也是个vector，取值{-1,1}，可以看到如果某个点i离超平面很远 时候，比如规定6.3中红色点的label取值为1，蓝色取值为-1，那么当点是属于红色的时候，Yi*（W‘X）是一个很大的整数，当点i是蓝色，Yi取值-11的时候，那么Yi*（W‘X）也是一个很大的正数。反正不会出现负数情况.

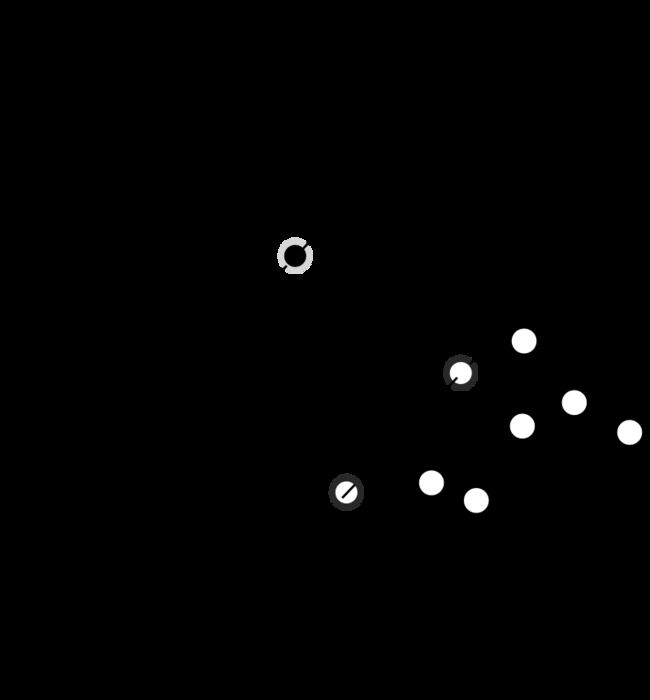
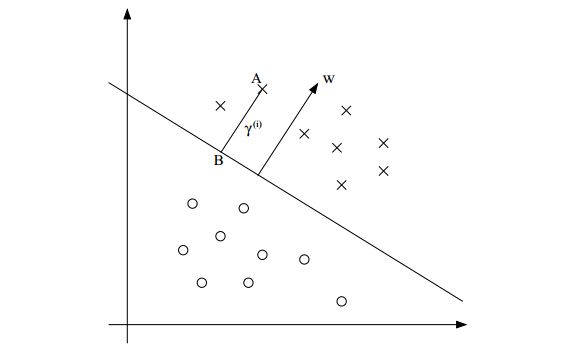
考虑到以下情况，如图所示：

上图中点A到超平面的距离假设为：

超平面的单位法向量为：

点A在超平面的投影点B，所以点B可以由点A来描述：。

由于点B在超平面上，所以满足：

那么就得到了：

那么任意一点到超平面的几何距离都可以表示为：

同时根据这个式子，可以发现，当缩放W和b的时候，比如w变成2w，b变成2b的时候，实际的几何距离表示并没有发生改变support vector到超平面的距离可以表示为：

那么我们的问题就可以变成：

从上图可以看到，两类的support vector之间的距离为：2/||W||

所以现在的问题就是要求  2/||W||的最大值，也就是求||W||的最小值，||W||是个平方根，所以求

跟原问题是一样的效果，系数1/2是为了数学计算上的方便而添加的，不影响结果。

此时问题就成了一个：

这是一个quadratic programming optimization 问题，可以用QP的解决方法来解决，但是为了使SVM便于扩展，从另外一个角度来解决此问题（Lagrange duality），这样带来的好处就是allowing us to use kernels to get optimal margin classifiers to work efficiently in very high dimensional spaces（我的理解就是便于引入核函数，使得SVM的用途更加广泛）。

7 什么是Lagrange duality？

Lagrange duality个人理解是分为2部分，首先是 Lagrange multiplier，然后就是duality。先来说说Lagrange multiplier

 7.1什么是 Lagrange multiplier？

Lagrange multiplier中文就是拉格朗日乘子，为什么要提到它？（http://en.wikipedia.org/wiki/Lagrange_multiplier）

在数学优化上，使用和引入拉格朗日乘子可以解决含有等式约束的问题，并找到这个问题的优解。

例如 含有等式约束的问题可以描述为：

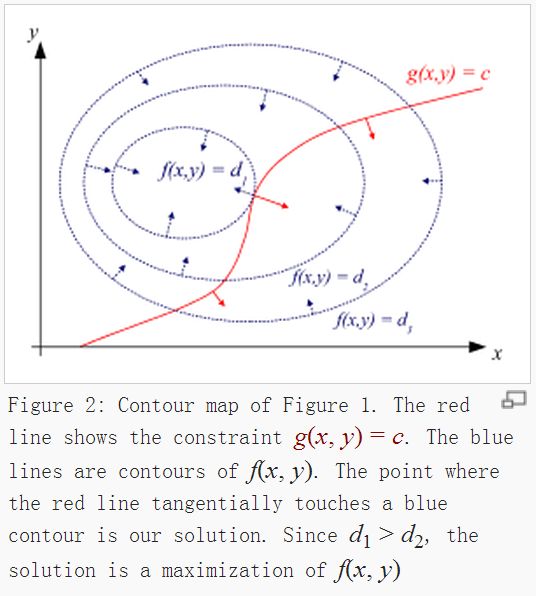
也就是求f(x,y)的最大值，约束条件为一个等式约束，g（x,y）=c

为了方便理解，上图说话

为了解决

引入一个变量（也就是拉格朗日乘子），得到一个新的式子，一般称为拉格朗日函数（Lagrange function）：

这样等式条件和原始问题就整合成到一个函数里面了。

要找到新问题的解，只需要对x、y、lambda分别求偏导即可，找出lambda，然后就可以得到驻点（x，y），从而找到目标点。

8 什么是duality？

每一个线性规划问题（称为原始问题）有一个与它对应的对偶线性规划问题（称为对偶问题），在线性方程中，圆问题的解与对偶问题的解是一致的。

举个简单例子来说：

工厂A有一些原材料a,b, 数量分别为100、300，可以用来生产甲、乙两种产品x，y，其中每生产一个甲产品，需要2个a和3个b，生成一个乙产品，需要4个a和5个b，每出售一个甲产品可以获利10元，出售一个乙产品，可以获利20元，问工厂A如何获利最高。

则可以的得到一个目标函数z=10*x+20*y,约束条件为不等式约束： x*2+y*3<=100,x*4+y*5<=300

以上问题先称作原始问题。

在考虑以下场景，此时来了另外一个工厂B，A工厂不想自己生产了，想把资源出售给B，此时，B希望能够以一个合理或者是较低的价格买进A的材料，A则希望在不损失自己的利益前提下出售自己 资源。

假设A出售原材料a的单位价格是m，出售b的单位价格是b，那么此时问题就是z，：

z=100*m+300*n，z越小越好，越小的时候，B才越高兴接受A卖出的材料，此外条件约束为不等式约束，2m+3n>=10(意义为，A用自己的材料生产甲材料保底为10元，所以把资源卖给乙，那么最低就不能低于10元)，4m+5n>=20(道理同上)。

有时候求问题不好直接求的话，求原问题的对偶问题可能会简单点，在某些条件下，对偶问题的解也就是原文提的解，相对对偶问题更深入一步了解的话可以自己找找资料学习了解下。

现在考虑一个一下问题：

称之为原问题，引入拉格朗日乘子：

由于h（w）=0.所以第三项对整个式子无影响，令a>=0,所以第二项整体是小于等于0的（a可以选择小于0，那么第二项的正好则变成负号，这对原问题无影响），那么原问题为p，则p可以描述为：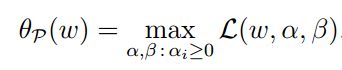

如果g（w）>0的话（a已经是大于0的了），那么显然

会得到（2）的结果。

所以

我们目标是求f（W）的最小值，所以：

这个新的描述跟原问题的目标一致

现在定义一个，令，也就是说是我们的原问题，只是形式做了替换

再来看另一个问题：

定义：

这里的下标D表示对偶（dual），那么

如果定义：

那么就是的对偶问题了，

此时：

（可以这样理解，一堆高个子小伙中最矮的那个小伙怎么也不比一堆最矮的小伙中最高的那个小伙矮）

可以看到，在特定条条件下，，此时可以用对偶问题代替原问题。

9 什么样的条件才算是特定条件？

先来看对偶问题，明显只有当对偶问题取到最大值的时候，也就是取到最优解的时候，和才有可能相等，因为总是大于等于的，此时比多了个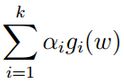，要想等式成立，那么就只要令a*g（w）=0了，这就是特定条件，也就是Karush-Kuhn-Tucker (KKT) conditions,

KKT：

第一个和第二个是 原问题和对偶问题取得优值的条件，第四和第五个是约束条件，第三个则是是原问题和对偶问题一致的条件。

10 求解最大

再回过头看之前的问题

对于约束条件做下调整得到

现在用KTT条件和拉格朗日乘子法求解这个问题，构造拉格朗日方程：

为了得到对偶问题，先将alpha固定，然后分别求偏导：

代入，得到：

其中第三项为0的，为内积，可以用来代替表示.

PS:本文的由来就是因为在ml in acthion一书中，不明白对偶问题的由来以及最终求解方程的由来，所以才有此文，简述下从原文提到对偶问题的推导，其实发现太挺简单的。

以下为推导过程：

那么就得到了只含有alpha的对偶问题了：

现在为了对偶问题的解与原问题一直，使用KTT条件，将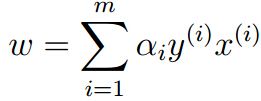代入，可以得到：

这样，当我们求出W和b后，对于任何一个新的数据，我们只需要计算即可，也就是要计算新的数据与所有已知数据的内积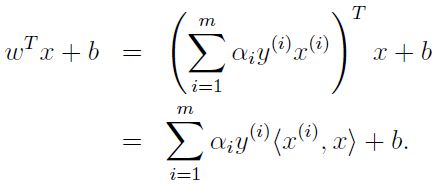

观察发现，对于非support vector来说，alpha均为0，所以要计算的就是所有的support vector与未知点的内积就可以了，这样就极大的减少了计算开销。

11 什么是Kernels，为什么我们需要它？

（http://www.quora.com/What-are-Kernels-in-Machine-Learning-and-SVM、http://www.quora.com/What-is-the-kernel-trick）

到现在为止，svm可以解决线性可分的问题，但是如果碰到线性不可分的问题，该怎么处理呢？比如像最开始的图6.1中的几种情况？

假设我们现在有一些1D的数据，

“A 1-dimensional hyper plane would be a vertical line. Clearly no vertical line can separate the given data set”，很明显在在1D情况下无法找到一个超平面（点）去分割数据，但是，如果对这些数据做一些处理（mapping）的话，比如，将原本1D的数据变成2D的数据的话：

那么数据在2D上就编程线性可分的了，图中的红线就是一个超平面。

所以面对线性不可分的情况下，处理方式就是将数据映射到更高维的空间中，这个变换过程中用到的函数就被称为核函数。

youtubu上有一个更加可视化（自备梯子后点我）的视频来帮助理解。（https://www.youtube.com/watch?v=3liCbRZPrZA#action=share）

“So the central idea is to be able to project points up in a higher dimensional space hoping that separability of data would improve. This mapping ( in our example  ) is called the Kernel function”

这位答主还提到：

“In practice we often map our data to very very high dimensional spaces using Kernels. In fact, certain Kernels like RBF kernel map data to infinite dimensional spaces. As you might be thinking, mapping and producing such high dimensional representation is a computationally daunting task. A related concept called Kernel Trick lets us pretty much bypass this computation cheaply. Kernel functions are almost never used without this Kernel Trick”

12 当数据投射到高维的时候，计算变得极其复杂了怎么办？

还是先从一个小例子来阐述问题。假设我们有俩个数据，x = (x1, x2, x3); y = (y1, y2, y3)，此时在3D空间已经不能对其经行线性划分了，那么我们通过一个函数将数据映射到更高维的空间，比如9维的话，那么 f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3)，由于需要计算内积，所以在新的数据在9维空间，需要计算的内积，需要花费O（n^2）。

在具体点，令x = (1, 2, 3); y = (4, 5, 6)，那么f(x) = (1, 2, 3, 2, 4, 6, 3, 6, 9)，f(y) = (16, 20, 24, 20, 25, 36, 24, 30, 36)，

此时 = 16 + 40 + 72 + 40 + 100+ 180 + 72 + 180 + 324 = 1024

似乎还能计算，但是如果将维数扩大到一个非常大数时候，计算起来可就不是一丁点问题了。

但是发现， K(x, y ) = ()^2

K(x,y)=(4  + 10 + 18 ) ^2 = 32^2 = 1024

俩者相等，K(x, y ) = ()^2=，但是 K(x, y ) 计算起来却比简单的多，也就是说只要用K(x, y )来计算，，效果和是一样的，但是计算效率却大幅度提高了，如：K(x, y )是O（n），而是O（n^2）.所以使用核函数的好处就是，可以在一个低维空间去完成高维度（或者无限维度）样本内积的计算，比如K(x,y)=(4  + 10 + 18 ) ^2 的3D空间对比 = 16 + 40 + 72 + 40 + 100+ 180 + 72 + 180 + 324 的9D空间。

13 为什么可以使用核函数？

因为svm最终计算的式子可以写出内积形式，所以任何可以写成内积式子的地方，都可以用核函数来代替去完成计算，从而大幅度提高效率。

0x0C什么样的函数才能被认为是有效的核函数呢？

这个问题展开又会是另外一个数学证明极其相关的东西了，主要是满足2个条件：

Generally, a function k(x,y) is a valid kernel function (in the sense of the kernel trick) if it satisfies two key properties:

• symmetry: k(x,y)=k(y,x)

• positive semi-definiteness.

（http://stats.stackexchange.com/questions/48506/what-function-could-be-a-kernel，感兴趣的同学可以研究下，我这种数学渣就暂时放下了）

目前来说，比较经典的核函数有以下几个。

高斯核函数（RBF）：Gaussian radial basis function maps the examples into an infinite-dimensional space（http://www.quora.com/Why-does-the-RBF-radial-basis-function-kernel-map-into-infinite-dimensional-space，这个涉及到泰勒级数展开）

多项式核函数:Although the RBF kernel is more popular in SVM classification than the polynomial kernel, the latter is quite popular in natural language processing (NLP).^[1][5] The most common degree is d=2, since larger degrees tend tooverfit on NLP problems(http://en.wikipedia.org/wiki/Polynomial_kernel)

当然还有其他核函数，就不一一列举了。

总之有些kernel function可以完成更好的工作，比如高斯核函数可以计算infinite D空间的俩个样本间的内积，显然在无限维的样本中，去计算内积是不可能的，但是却可以在一个低维度的空间完成无限维空间中样本的计算。

这应该核函数的价值了（我的理解）

14 碰到有些数据就是比较拽（线性不可分）怎么办？

虽然通过核函数，可以将数据映射到高维空间，然后寻找超平面，但是也不能保证100%可以找到“理想”的超平面

(While mapping data to a high dimensional feature space via φ does generally increase the likelihood that the data is separable, we can’t guarantee that it always will be so)

比如以下这种情况：

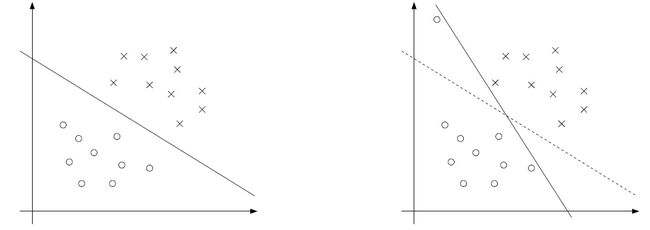
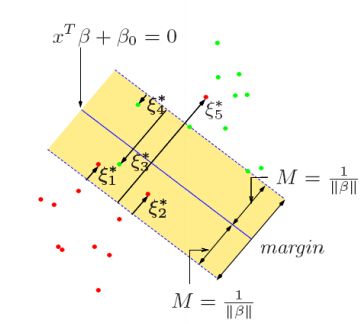
上面两幅图可以看出，很明显，左边的那条线才是我们想要的，右边的实线因为左上角的一个数据而从虚线位置偏转到现在的位置，虽然能“ 完美”划分数据，但是很明显左边图的实线才是当前数据集的最佳超平面。

为了针对这种情况，所以引入一个新的变量，称作slack variable  ξ （ ξ > 0）（松弛变量），

之前的目标：

现在的目标则为：

为了便于理解，找了附图：如下

当有一些比较“特殊”的点落在margin内或者在超平面的另外一侧的时候，那么ξi就大于0，当点都比较听话的时候，ξi就等于0，那常量C是个啥呢？

C主要是用来控制相对权重，目的是来保证目标函数最小值

（The parameter C
controls the relative weighting between the twin goals of making the ||w||^2 small (which we saw earlier makes the margin large) and of ensuring that most examples have functional margin at least 1.）

同样的，构造拉格朗日方程

然后利用拉格朗日乘子法对w, b, ξ分别求导数，便可以得到以下的对偶形式方程了：

此时的KTT条件为：

当alpha>0,也就是说，=0，此时的数据点就是有资格作为support vector，这这种条件下，

如果,,那么，此时,，那么在这个条件下的点就是"特殊点"，比如上图中的了。

如果,那么,此时,，可以看出是最小值(这里就体现了C的价值了),那么在这个条件下的点就是正好在超平面上的点了

当alpha=0的时候，很明显这些点都不满足作为support vector 了。

15 问题都搞的差不多了，那怎么求解目标呢？

一位名为John Platt的大神，给出了一个有效的解决方案，名为SMO算法(sequential minimal optimization)

16 SMO

大神的原文请戳我（自备小梯子）

解决目标问题有多种方式，但是效率比其他的要好，原因：Sequential Minimal Optimization (SMO) is a simple algorithm that can quickly solve the SVM QP problemwithout any extra matrix storage and without using numerical QP optimization steps at all。

SMO主要就是干了两件事情，1是每次迭代过程中解决2个拉格朗日乘子，2是启发式寻找下一次要解决的的拉格朗日乘子（a heuristic for choosing which multipliers to optimize）

为什么要一次同时解决两个拉格朗日乘子呢？

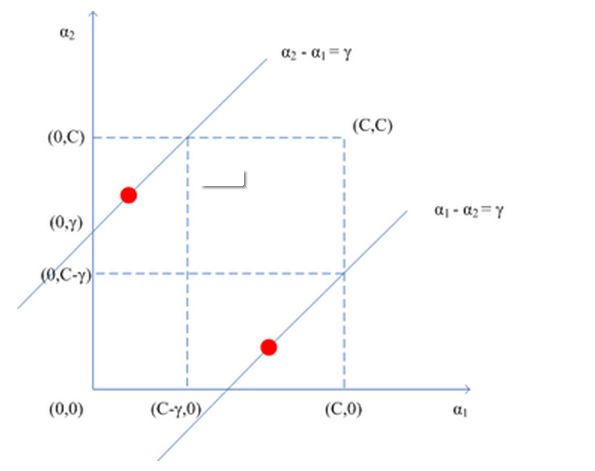
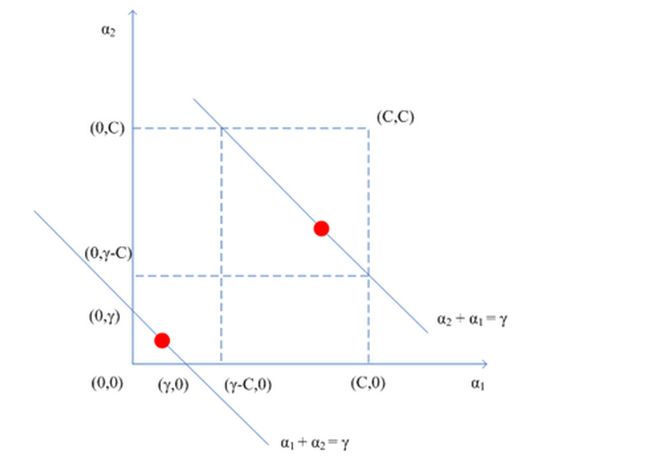
根据约束条件，可以得到，因为每次针对2个变量，所以其他变量视作常数。当与异号的时候，约束条件就成了上面的第一幅图所示，同号的话就如第二幅图所示。

所以 的取值下限为：,上线值为：。同理当与同号的时候，上下限的值也都能相应表示出来。

然后将用来表示：

所以

然后对展开后的W经行求导，便可以得到，但是要满足已有的约束条件，假设新得到的=,那么有以下约束：

得到新的后，就可以得到新的。

的具体求法比较简单，

现在将、代入到W中求导可以得到：

,

其中，,表示迭代前的值。

继续化简可以得到(导数等于0)：

,其中，，也就是预测值与已知值的误差，

求得新的后，便可求得新的，

从中可以看出，,也就是两点间的相关性（也可以简单理解为距离）。

当求得，可以求得在下的的更新，同时得到后也可以得到一个下的更新。

根据KKT条件，在KKT条件下，每当得到一个新的alpha后，必须使得输入的输出结果为，

所以有：

在每次进行迭代前有：,

也就是说：,代入

可得：

,其中，

最后得到

原文如下：

PS：另外还发现二阶导数在正常情况下是大于0的，一阶导数单调，有兴趣的可以在这个上面在细究下：)

Python简单版代码如下：

def simplesvm(datMat,labelMat,C,toler,maxiter):
    dataMatrix=np.mat(datMat)#100X2
    labelMat=np.mat(labelMat).transpose()
    b=0
    m,n=np.shape(dataMatrix)
    cycle=0
    alphas=np.mat(np.zeros((m,1)))
    while cycle toler) and (alphas[i] > 0)):

                j = selectJrand(i,m)

                fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej=fXi-float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H:
                    print "L==H"
                    continue
                eta=2.0*dataMatrix[i]*dataMatrix[j].T-dataMatrix[i]*dataMatrix[i].T-dataMatrix[j]*dataMatrix[j].T
                print 'a',eta
                if eta>0:
                    print "eta>=0"
                    continue
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    #print "j not moving enough"
                    continue
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*\

dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T -labelMat[j]*(alphas[j]-alphaJold)*\
                            dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                #print "iter: %d i:%d, pairs changed %d" % (cycle,i,alphaPairsChanged)
        if (alphaPairsChanged == 0):
            cycle += 1
        else:
            cycle=0
        #print "iteration number: %d" % cycle
    return b,alphas

上面的代码并不是完整版的SMO过程

完整版的过段时间再学习下。

整个过程中参考了很多谷歌和百度上优秀的文章帮助理解，限于数学水平实在有限，只能理解到这儿了。后面还有从二元分类扩充到多元分类的，有时间再接着补充。

文章主要框架是照着ML in action和AndrewNg的一个SVM的pdf来写的，同时很多概念的理解比如b的更新，以及a的范围理解参看其热心网友帮助，十分感谢。

http://www.pstat.ucsb.edu/student%20seminar%20doc/svm2.pdf

PS:http://private.codecogs.com/latex/eqneditor.php 一个好东西