超详细 | 贝叶斯网络基础——有图有真相

Hello，大家好，我是starz。这是本系列的第二篇《概率基础Ⅱ》，虽说是概率基础，但作为过渡，它开始以图为载体

这节的主要内容有：

1. 贝叶斯网络

2. 三种结构

3. D-划分

4. 贝叶斯球

5. 马尔科夫毯

6. 应用例子

7. 总结

让我们开始吧 :3

贝叶斯网络

概率图模型可笼统分为两类，一是基于无向图的马尔科夫网络：

二是基于有向图的贝叶斯网络：

事实上，我们可以通过一些特殊的手段^[1]^将贝叶斯网络转化为马尔科夫网络，同时保留贝叶斯网络各个变量之间的条件独立性

因此马尔科夫网络相对来说更泛化抽象，它不在我们的讨论范围内 :)

Anyway，笼统说来：贝叶斯网络 = 有向图 + 概率

如果想精准一点^[2]^，我们可以说：

其中：

1. BN指贝叶斯网络，DAG指有向无环图，CPDs指条件概率分布

2. DAG的作用是——作为变量间条件独立性的定性表示

3. CPDs的作用是——作为变量间条件独立性的定量表示

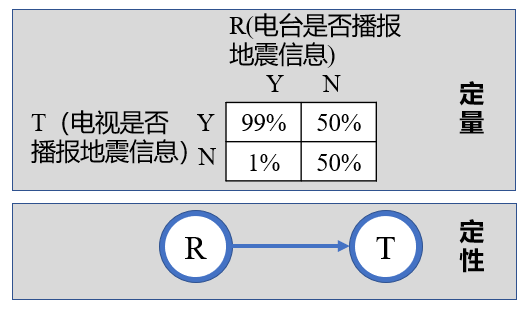
定性指的是，如果在有向图中两个变量R和T之间有弧，则表示这两个变量相关。例：若R和T之间存在R指向T一条弧，则说明R在一定程度上影响了T的取值（弧即箭头）

定量指的是，模型用条件概率分布中的概率值规定了变量间取值的关系

如下，图中箭头表明了R和T之间的关系，条件概率（表）给出了两者的定量关系：

三种结构

俗话说万物皆有联系，但如果在贝叶斯网络中，任意两个节点都有弧的话，推断学习等任务就会变得非常困难

于是乎，前人提出了许多条件独立性假设用于简化运算，如：

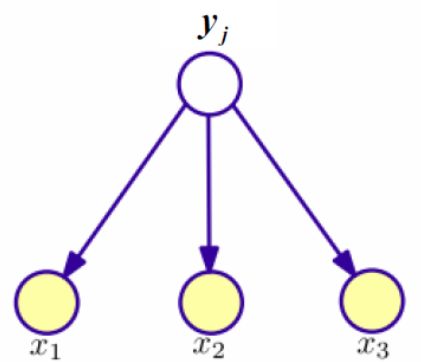
1. 属性条件独立性假设，即变量X之间是相互独立的，反应在图中就是X之间没有弧，如：

   朴素贝叶斯，

   

2. 马尔科夫假设，即变量X只取决于前K个变量，如：

   一阶马尔可夫假设，当前变量只取决于前一个变量，

   

3. 变量集合间的条件独立性假设，如：

   贝叶斯网络，当前变量X只取决于其父母，

   

如何直观理解贝叶斯的条件独立性假设呢？

接下来，我们从贝叶斯网络的三种基本结构入手，试图用语言阐明：独立性在贝叶斯网络的局部是如何存在的

即以下公式在三种结构中都成立

例子中的随机变量说明：

1. B：Burglary，表示是否被盗窃

2. E：Earthquake，表示是否有地震

3. A：Alarm，表示小区是否有警报声

4. R：Radio，表示电台是否在播报地震信息

5. T：TV，表示电视机是否在播报地震信息

以下我们将弧看作信息流动过程

链式结构

主角是：T

T和E本身是相关的

信息流动的方式是：

1. E：发生地震

2. E -> R：电台接到信息后，播报地震消息

3. R -> T：电视台接到信息后，播放地震消息

T和E的关系是显而易见的。在没有其它观测的情况下，假设发生了地震，电视台^注1^播报地震消息的概率会升高；假设没发生地震，电视台播放地震消息的概率会降低

在R得到观测后，T和E条件独立：

假设R被观测，R说“地震啦”，因为图中没有其它路径可以提供E的真实信息给T，那么不管E到底有没有发生，T都会基于R提供的信息播放地震消息

这就是：在链式结构中，两端变量原本相关，在中间变量被观测的情况下，两端变量条件独立，即

公式释义

E和R都提供信息给T的情况下，把E的信息量去除，不会给T的分布带来任何变化

换而言之，T只听它妈的

分叉结构

主角是：R

R和A本身是相关的

信息流动方式是：

1. E：发生地震

2. E -> R：电台接到信息后，播报地震消息

3. E -> A：小区接到消息后，开启警报

考虑以下场景来分析R和A的相关性：

假设小区的警报响了，地震的可能性增大，电台播报地震消息的概率相应提高；假设小区警报都没响，地震的可能性不大，电台播报地震消息的概率相应降低

在E得到观测后，R和A条件独立：

假设E被观测，E说“地震啦”，R和A都得到了来自E的确切消息，做出什么反应取决于它们各自跟E的条件概率分布，和对方的相关性被消除

这就是：在分叉结构中，两端变量原本相关，在中间变量被观测的条件下，两端变量独立，即

V型结构

主角是：A

B和E本身是无关的：

信息流动方式是：

1. E：发生地震

2. B：发生抢劫

3. E -> A：小区接到E消息，开启警报

4. B -> A：小区接到B消息，开启警报

在没有其它观测的情况下，B和E是无关的，如果有人说：啊祸不单行，今天被抢劫了，或许地震也会来一下。我们会觉得这人莫名其妙

在A得到观测后，B和E相关：

假设A被观测，警铃响了，那么很大可能E和B之间发生了一个，若E没有发生，B发生的概率就会升高，反之亦然

这就是：在V型结构中，两端变量原本不相关，在中间变量被观测的条件下，两端变量相关，即

小总结

我们可以看到贝叶斯网络的条件独立性假设在局部结构下的释义是很自然的。将这个性质和链式法则结合在一起，就能推出贝叶斯网络的因子分解形式：

D-划分

D-划分的作用是：判断贝叶斯网络在给定某些观测的情况下，两个变量，或变量集合，是否相关

有两个小细节可以帮助理解：

1. 它是上节描述三种结构性质的一种泛化，使得它能用在变量集合上

2. “被D划分”的意思就是两个变量、或变量集合，独立或条件独立

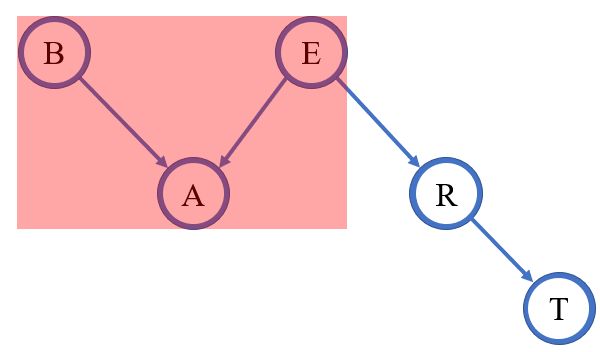
用我们的老朋友来理解一下D划分，注意到红色外边框的意思是它既可以是个节点，也可以是一个节点集合：

类似的，我们考虑三种情况：

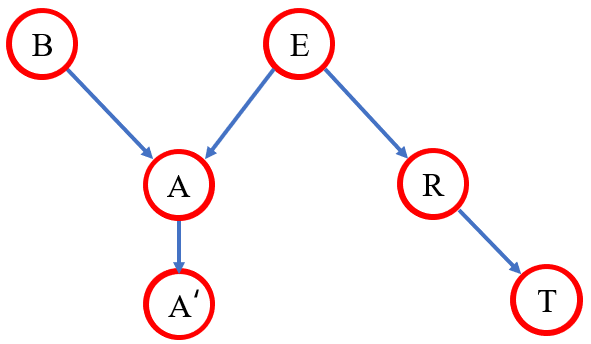
1. B和E被D划分的情况：因为连接B和E的通道只有个通过节点A的V型连接，那么只要A或者A'不被观测到，B和E就是独立的（因为假设A’被观测到，信息会往上传播到A）

2. A和R被D划分的情况：因为连接A和R的通道只有通过E的分叉连接，那么只要E被观测到，A和R就是条件独立的（分叉连接的中间变量被观测则两端的变量独立）

3. E和T被D划分的情况：因为连接E和T的通道只有通过R的链式连接，那么只要R被观测到，E和T就是条件独立的

贝叶斯球

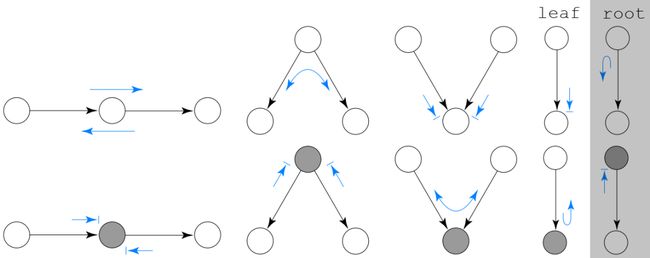
理解了以上的内容，我们就可以打贝叶斯球啦。贝叶斯球是一种理解D划分的趣味运动，让我们来了解一下十条规则：

其中：→表示在这个位置球可以通过，而→|表示球不能通过

看起来挺唬人，但其实内容我们已经讨论过了，球其实就是前面提到的信息，而十条规则可以分成三个部分来理解：

1. 灰色部分是喜闻乐见的三种结构，上三代表中间节点没有被观测，下三代表中间节点被观测

   

2. 灰色部分表示的是球到叶子节点（即没有孩子的节点）的情况，如果叶子节点没被观测，则球阻塞，但如果叶子节点已经被观测，它会回弹，例如回弹至V型结构的中间节点，它会改变V型结构两端变量的条件独立性

   

3. 灰色部分表示的是球到根节点（即没有父代节点）的情况，如果根节点没被观测，则球要回弹，但如果根节点已经被观测，那么有两种情况，要么是V型连接的两个端点其中之一，要么是链式结构的上游端点，这两种情况下变量的观测都不能为其它节点的信息带来增益，所以令球阻塞

   

了解了规则之后，让我们来到简陋的球场^[3]^：

有五个任务：

1. 给定观测X2，尝试从X1把球打到X4

2. 给定观测X1，尝试从X2把球打到X5

3. 给定观测X2，尝试从X1把球打到X6

4. 给定观测X1、X6，尝试从X2把球打到X3

答案是3和4是可以把球打过去的，1和2为什么不行大家可以分析下

下面给出第三小问的答案，其中灰色的X2为被观测变量：

第四小问的答案，其中灰色的X1和X6为被观测变量：

马尔科夫毯

节点A马尔可夫毯的定义为一个节点集合，这些节点被观测的情况下，节点A与其余的节点（除去A和它的马尔科夫毯）条件独立

也就是说，我们把节点A身边的马尔科夫毯节点置为灰色，那么从其它节点出发的贝叶斯球都打不过来A这边

玩多了贝叶斯球你就会发现，C的马尔科夫毯 = C的孩子 + C的父母 + C的配偶们

注：

1. C的孩子需要被观测到，因为要堵住以C和X8两个变量形成的链式结构和V型结构带来的信息传播

2. C的父母需要被观测到，因为要堵住以C和X5两个变量形成的链式结构和分叉结构带来的信息传播

3. C的配偶们需要被观测到，是因为抓小三有助社会和谐要堵住配偶们通过被观测的孩子们对C的信息传播

4. 以上为个人理解，如有错漏请在公众号后台回复

例如下图的X4, X5, X6, X7, X8, X9就是节点C的马尔科夫毯

应用例子

基于以上内容，我们已经对贝叶斯网络有了个初步的了解

生活中很多问题都可以用贝叶斯模型来建模，甚至我们还可以使用贝叶斯网络来辅助我们玩游戏！

鉴于我们学得比较浅，目前只能帮我们玩玩扫雷

扫雷^[4]^，是一款单人的电脑游戏。游戏目标是找出所有没有地雷的方格，完成游戏；要是按了有地雷的方格，游戏失败。游戏以完成时间来评高低

在原始的游戏设定中，如果点击没有地雷的方格会显示附近地雷的数量N

如果把N看成观测变量，而当前位置以及附近有没有地雷看作隐藏变量，从这个角度看来，扫雷是一个基于观测变量推断隐藏变量的游戏

为了简化题目，我们将二维度的游戏转化为一维，游戏由由 1×4 个小格组成，示意图如下：

虽然建模这个东西听起来有点复杂，但是没有关系，根据前文： 贝叶斯网络 = 有向图 + 条件概率分布，我们分两步来完成：

有向图部分

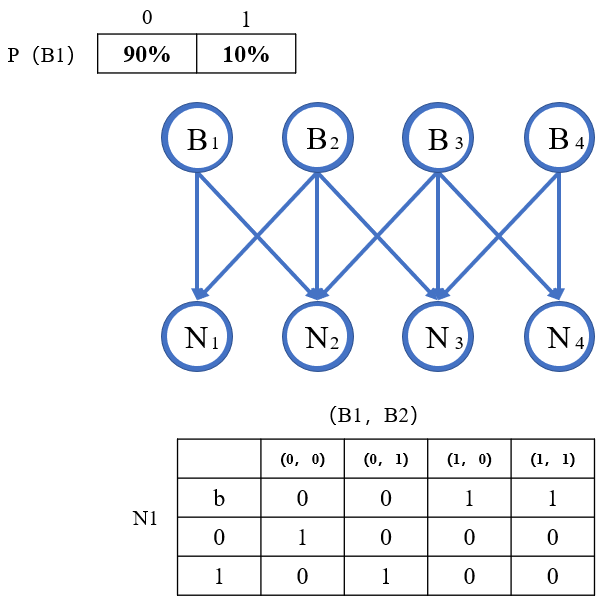
先定义几个变量，总共有四个格子，每个格子有一个观测变量和一个隐含变量，总计8个变量。我们用BI表示第i个格子是否有炸弹，用Ni表示第i个格子显示的数字，因为当前位置的观测结果取决于身边两个位置隐藏变量的取值，那么它们之间的关系如图所示：

有趣的是，有向图中形成的是V型结构^注1^，这在游戏中的体验一致：在不知道N的情况下，B1、B2和B3的取值之间是相互独立的；而知道了N2的取值后情况就大不相同，如N2 = 2，则B1和B3一定有炸弹

条件概率分布部分

假设每个格子有炸弹的概率是10%，有：

注：

1. 其中b为Bomb，挖出炸弹的意思

2. 这里只贴了红色两条边对应的条件概率，有兴趣大家可以把其它边也写一写

总结

这篇文章主要介绍了：

1. 贝叶斯网络是什么

2. 贝叶斯网络的条件独立假设是怎么蕴含在三种基本结构中的

3. 如何判断贝叶斯网络中变量之间的独立性

4. 如何建立自己的贝叶斯网络

后续的文章的内容会包括：

1. 推断问题——手头有完整的贝叶斯网络（有向图 + 条件概率），以及一把证据，如何根据已有证据进行推理

2. 参数学习——手头有残缺的贝叶斯网络（只有有向图），如何根据数据集，让网络在数据集中学习参数（条件概率）

3. 结构学习——手头啥都没，如何根据数据集，让算法自己学习贝叶斯网络的结构（有向图）和参数（条件概率）

希望我们能把它讲清楚，谢谢观看

注：

1. 东京电视台除外

2. 除非输了，不然隐变量对于玩家来说是不可见的，即不会出现Bi被观测的情况，所以探究以Bi为中心的分叉结构在这个问题设定下没有意义

Reference

[1] 白板机器学习第九章《概率图模型》

[2] Probabilistic Graphical Models，Philippe LERAY

[3] (기계 학습, Machine Learning) Week 7 Bayesian Network | Lecture 4 Bayes Ball Algorithm

[4] https://zh.wikipedia.org/wiki/踩地雷

​