回归分析
1、回归分析分类
包括线性回归、非线性回归、逻辑回归(0和1)、岭回归、主成分分析,最后两个参与建模的自变量之间具有多重共线性,但是岭回归的X非常多
2、一元线性回归建模
比如:淘宝某商品的总销量和收藏数的一元线性回归
第一步:绘制散点图看数据是否有异常数据
Yvar=df[因变量名称]
Xvar=df[自变量名称]
plt.scatter(Xvar,Yvar)
去除异常点后重新做散点图检验
再做散点图时要加上拟合线:
plt.plot(x1,y,“r”)
第二步:一元线性回归建模-OLS最小二乘法
import statmodels.api as sm
Y=Yvar.values
X=Xvar.values
X=sm.add_constant(X) #因为OLS没有常数项,也就没有b,这个操作可加上常数项
lm=sm.OLS(Y,X).fit()
print("因变量:因变量列名称”)
print(“自变量:自变量列名称”)
print("==========一元线性回归结果===========“)
print(lm.summary())
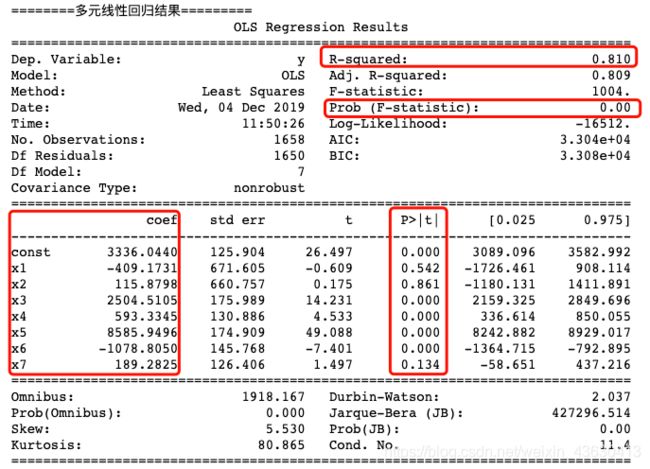
得到的结果中最重要的四个量:一是R-squrred(反映线性拟合结果好还是不好,介于0-1,越接近1,拟合结果越好),二是Prob(F-statistic)代表整个结果显著性水平,必须要<0.05,否则整个结果不被接受,三是常数项系数,显著性水平也要小于0.05,否则常数项不被接受 ,四是x1系数
3、数值参数的多元线性回归
第一步:检查Xvar中各列异常值(通过作散点图,Xvar中有多少个自变量,就有多少个散点图)
Xvar=df[[所有自变量名称]]
Yvar=df[因变量名称]
for I in Xvar.columns:
print(i)
plt.xlabel(i)
plt.ylabel("因变量”)
plt.scatter(Xvar[i],Yvar)
plt,show()
去除异常点后重新做散点图检验
第二步:通过热力图,查看自变量与因变量之间以及自变量之间的相关系数,初步探索相关性
#相关系数表
t=df[[所有自变量名称+因变量名称]]
import seaborn as sns
t.corr()
#作所有自变量和因变量的热力图
plt.figure(figsize=(10,8))
sns.heatmap(np.abs(t.corr()),annot=True)
plt.show()
第三步:多元回归建模
#归一化
from sklearn.preprocessing import StandardScaler
std=StandardScaler()
Xstd=std.fit_transform(Xvar)
#对归一化结果进行建模
import statsmodels.api as sm
Y=Yvar.values
X=Xstd
X=sm.add_constant(X)
lm=sm.OLS(Y,X).fit()
print("========多元线性回归结果=========")
print(lm.summary())
4、降维:主成分分析
减少分析因素,我们知道一个结果的决定因素有很多,但是重要性却各有不同
降维的本质就是保留主要因素,融合次要因素,删除微弱元素
from sklearn.decomposition import PCA
#设置主成分的数量,就是说要降到几个维度
pca_model=PCA(n_components=3)
#给出XY
Y=Yvar.values
X=Xstd
#执行PCA方法
pca_model.fit(X)
#取得降维后的x
X_pca=pca_model.transform(X)
#回归的固定代码
X_pca=sm.add_constant(X_pca)
lm=sm.OLS(Y,X_pca).fit()
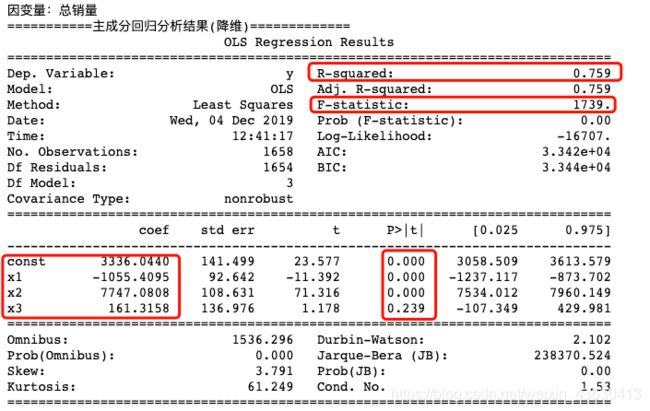
print("因变量:总销量")
print("===========主成分回归分析结果(降维)=============")
print(lm.summary())
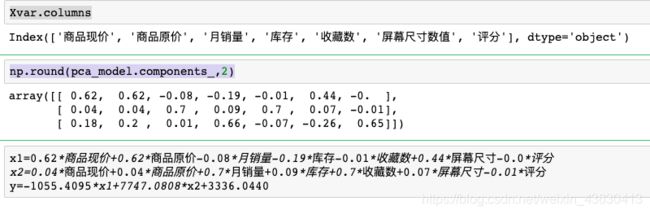
Xvar.columns
#显示出各维度与各X自变量关系的系数
np.round(pca_model.components_,2)