概率论第2记:随机变量1
从这一章开始,概率统计进入高数的研究范围。打起精神吧
什么是随机变量?
如果我们先后抛掷两颗骰子,所有可能的样本空间S={(1,1),(1,2)…(2,1)…(6,6)},很多时候我们关心的不是样本空间,也不是先后抛出了多少点,而是关注两个骰子的点数加起来是多少点,比如加起来是5点的有(1,4)(2,3)(4,1)(3,2).这样,就是样本空间和具体的数值之间建立了某种关联,这个数值如果用字母X表示,就称X是建立在样本空间S上的随机变量。所以随机变量的定义为:定义在样本空间S上的实值单值函数:X=X(x),(x∈S).
比如打靶,着弹点距离靶心的距离就是一个随机变量(假设目标靶直径人,而且每次射击不会脱靶):X((x,y))= x 2 + y 2 , x 2 + y 2 < = r 2 \sqrt{x^2+y^2},x^2+y^2<=r^2 x2+y2,x2+y2<=r2很显然,随机变量的取值也有一定的概率性。
离散型和连续型随机变量
随机变量的取值是否可以列举,是区别二者的标志
对于离散型随机变量:
pi>=0
∑ k = 1 ∞ p k = 1 \sum_{k=1}^{∞}{p_{k}=1} ∑k=1∞pk=1
两种重要的离散型随机变量
二项分布
样本空间只有两个结果{H,L},这样的实验称为贝努利实验。这样的实验进行n次,就是n重贝努利实验。设样本空间某实验结果(H或者L,这里我们假设是H)出现的概率为p,那么n重贝努利实验中,出现k次H的概率为:P(X=k)= C n k ∗ x p ∗ ( 1 − p ) n − k \textrm{C}_{n}^{k}*x^{p}*(1-p)^{n-k} Cnk∗xp∗(1−p)n−k,称X服从以n,p为参数的二项分布。特别的,当n=1时候,P(X=k)= p k ( 1 − p ) 1 − k p^k(1-p)^{1-k} pk(1−p)1−k
泊松Poisson分布
P(X=k)= λ k e − λ k ! \frac{\lambda ^ke^{-\lambda }}{k!} k!λke−λ
很多随机变量服从或近似服从泊松分布,比如一天中医院挂号的人数。
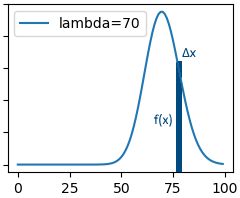
泊松分布,当k= λ \lambda λ时,函数取最大值。以下是不同 λ \lambda λ的泊松分布函数图(虽然是离散型随机变量,但是,此处以连续的函数图形直观说明)

实现以上图形的Python代码如下:
from math import *
import matplotlib.pyplot as plt
def Poisson(K,l):
return ((l**K)*exp(-1*l))/factorial(K)
_lambda=[10,30,50,70]
for i in range(4):
test_data=[]
subplt=plt.subplot(2,2,i+1)
for j in range(100):
test_data.append(Poisson(j,_lambda[i]))
subplt.plot(test_data,label="lambda=%d"%_lambda[i])
subplt.Xlabel="X=k"
subplt.Ylabel="Posisson"
subplt.legend()
plt.show()
PS:实际上,以上两种分布的公式,如果看作连续型随机变量的话(尽管实际上不是),函数都是概率密度函数,因为: ∑ f = 1 , ∫ f d x = 1 \sum {f}=1, \int {fdx}=1 ∑f=1,∫fdx=1
上面提到了概率密度函数,下面接着写。
连续型随机变量
连续型随机变量和离散型随机变量的重要区别:离散型随机变量X的取值是当x为样本空间某一随机事件(包含基本事件)X的概率值。连续型随机变量的值是x在某一取值区间时候X的概率值(因为样本点不可列举),而在某一确切的x值,X为0,从这个表述可以看书,连续型随机变量的取值实际上是某一个函数在区间的积分:
P ( a ⩽ x ⩽ b ) = ∫ a b f ( x ) d x P(a\leqslant x\leqslant b)=\int_{a}^{b}{f(x)dx} P(a⩽x⩽b)=∫abf(x)dx
而且有: ∫ a b f ( x ) d x ⩾ 0 \int_{a}^{b}{f(x)dx}\geqslant0 ∫abf(x)dx⩾0
∫ − ∞ ∞ f ( x ) d x = 1 \int_{-∞}^{∞}{f(x)dx}=1 ∫−∞∞f(x)dx=1
f(x)称为X的概率密度(函数),在计算X落在某一区间的概率时候,可以不必考虑是否包含区间的端点,毕竟端点积分为0,所以:P{a≤X≤b}=P{a
三种重要的连续型随机变量
平均分布
X在区间(a,b)内平均分布,区间外概率为0:
f(x)= { 0 if x = 其 他 1 b − a if a ≤ x ≤ b \begin{cases} 0 & \text{ if } x= 其他\\ \frac{1}{b-a} & \text{ if } a≤x≤b \end{cases} {0b−a1 if x=其他 if a≤x≤b
指数分布
X具有概率密度:f(x)= { 0 if x = 其 他 1 β e − x β if x > 0 \begin{cases} 0 & \text{ if } x=其他 \\ \frac{1}{\beta }e^{\frac{-x}{\beta }} & \text{ if } x>0 \end{cases} {0β1eβ−x if x=其他 if x>0
比如电子元件的寿命就服从指数分布
正态分布
也叫高斯分布
百度百科这么说:若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
![]()
这个分布以后详解