Memory Networks原理及其代码解析

    http://blog.csdn.net/u011274209/article/details/53384232

原理：

文章来源：Memory Networks 、 Answering Reading Comprehension Using Memory Networks

  对于很多神经网络模型，缺乏了一个长时记忆的组件方便读取和写入。作为RNN，lstm和其变种gru使用了一定的记忆机制。在Memory Networks的作者看来，这些记忆都太小了，因为把状态（state，也就是cell的输出）及其权重全部都嵌入到一个低维空间，把这些知识压缩成一个稠密的向量，丢失了不少信息。这也是文章（或者memory系列）的出发点，它的做法简单粗暴，增加一个m模块。m是一个对象的数组（an array of objects，for example an array of vectors or an array of strings），在文章里，更多叫成slot（插槽）。记忆一个事实（一般是对话组里的一句话），就把它“插”到记忆（数组）里。
  一个记忆网络（memory networks，简称为MemNN），包括了上述的记忆m，还包括以下4个组件I、G、O、R（是不是超级像lstm的三个门啊，然后m像cell的list）：

组件	名称	描述
I	input	converts the incoming input to the internal feature representation.
G	generalization	updates old memories given the new input. “We call this generalization as there is an opportunity for the network to compress and generalize its memories at this stage for some intended future use.”
O	output	produces a new output in the feature representation space given the new input and the current memory state.
R	response	converts the output into the response format desired – for example, a textual response or an action.

I：用于将输入转化为网络里内在的向量。作者使用了简单的向量空间模型，维度为3*lenW+3（熟悉VSM会问为什么不是lenW，下面会说具体）。
G：更新记忆。在作者的具体实现里，只是简单地插入记忆数组里。作者考虑了几种新的情况，虽然没有实现，包括了记忆的忘记，记忆的重新组织。
O：从记忆里结合输入，把合适的记忆抽取出来，返回一个向量。
R：将该向量转化回所需的格式，比如文字或者answer。对于R来说，最简单的是，直接返回o的第一个支撑记忆，也就是一句话。当然作者，打算弄复杂点，返回一个词汇w。

  以下是统一的公式（可以看出作者把这玩意做成了一个架构，而不是一个具体的算法）：

  所有组件都是神经网络的话，叫做记忆神经网络（MemNNs，多了个s）。

Basic Model：

  这是作者自己做的一个基本模型，或者算作是这个架构的一个简单例子。以下从一个记忆四个组件的角度，对这个方法进行说明：

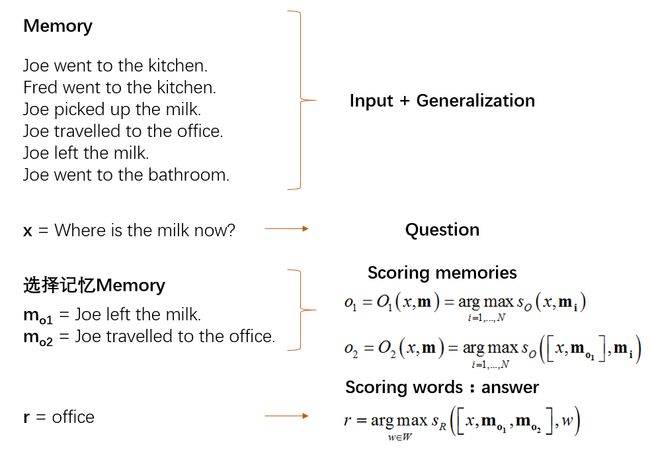
I：I输入的是一句话，简单地将I转换为一个频率的向量空间模型。
G：也是如上，简单地把读到的对话组里的每一句话的向量空间模型，插到记忆的list里，这里默认记忆插槽比对话组句子还多。 mN=x , N=N+1 。是的，m、I和G都很简单，也就是重任就压到了O和R上了。
O：O干的事，就是输入一个问题x，将最合适的k个支撑记忆（the supporting memories，在下文的数据集里会举出例子），也就是top-k。做法就是把记忆数组遍历，挑出最大的值。最后，O返回一个长度为k的数组。
对于top1有 o1=O1(x,m)=argmaxi=1,...,NsO(x,mi)
对于top2有 o2=O2(x,m)=argmaxi=1,...,NsO([x,mo1],mi)
  这里有几点说明：1、在这里，返回的 oi 简单就是记忆数组的序号索引。
  2、在这里（向量空间模型向量表示），有 sO([x,mo1],mi)=sO(x,mi)+sO(mo1,mi) 。也就是对于多事实的情况，可以分开同时计算其与记忆的“关联度”，然后加总。如果对于其他向量表示方式，则不一定有这样的线性关系。
  3、作者给了一个有趣的例子反映了这个预测（test）过程，我觉得与其叫做回忆过程，还不如叫成推理过程好些，囧：


  R：为了返回一个词汇w，设置公式 r=argmaxw∈WsR([x,mo1,mo2],w) 。这里对所有的词汇进行循环遍历，挑出最适合答案（分数最高）的结果。在论文里，词汇被转化为同一空间里的向量空间模型的向量。如“memory”= [0,0,0,0,1,0,0,0] ，“network”= [1,0,0,0,0,0,0,0] ，则句子“memory network”= [1,0,0,0,1,0,0,0] 。
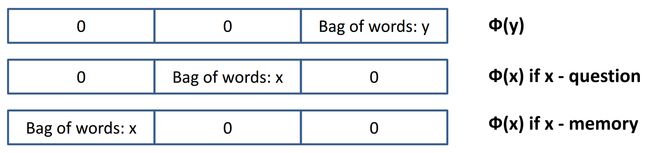
  最后：作者继续简化处理 sO=sR=s(x,y)=Φx(x)⊤U⊤UΦy(y) 。
  其中，U是一个权重矩阵，维度为n*D。D是输入向量的维度，n是嵌入的维度，n是一个超参数。作者使用D=3*lenW的维度。这里考虑了3倍向量空间模型长度，一份是给了phi_y Фy ，一份是给了x是输入的问题时的phi_x Фx ，一份是给了x是支撑记忆时的phi_x Фx ，三份直接连接在一起就可以了。（个人认为，作为对称，应该是4份。或许作者认为问题是一个空间，陈述句是另一个空间，而回答词汇只是属于陈述句空间，不用放在一起。） 和 使用不同的权重矩阵。

  训练过程：使用margin ranking loss和sgd，在SVM和TransE里已经见识过了，就不赘述，复制公式如下：

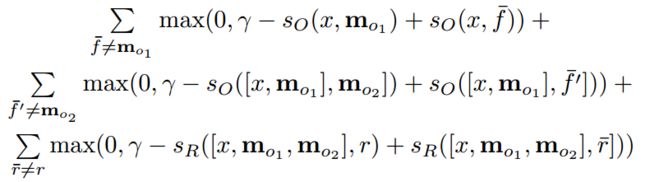
   f¯ 、 f¯′ 分别是第一和第二个支撑记忆， r¯′ 是正确答案。对的，读者也发现了，MemNN是一个监督学习的算法。（以后很多记忆模型，改成了弱监督了，以N2N为代表）注意，这里有两个监督的部分，一个是支撑记忆，一个是正确答案。

basic model的改进

  作者考虑了一些新的情况：包括
  1、输入是连续的词汇。使用RNN之类的产生一些词序列，作者加了一层，叫做segment。
  2、在G的时候，我们是简单把原向量“插进”记忆数组里，如果是把向量“hash”进去呢？
  3、考虑写入的时间。由于下面的代码使用了这个情况，在这里就多讲述。作者针对这种情况的方法是增加了3个维度的，D=3*lenW+3。加上存在一个输入 x ，一个记忆 y 和另一个记忆 y′ 如图：

  这里3个维度分别代表：x is older than y，x is older than y′, y older than y′，这里xyy’可以是问句也可以是陈述句。
  在训练之前三个维度都为0。训练的时候，对于三种情况，如果都符合，则都赋予1。特别的，如果x是问句时，则前两个维度都置为0，因为问句一定是最新的。
这时O的公式改变了，（R仍然不变，见上文）：
sOt(x,y,y′)=Φx(x)⊤Uot⊤Uot(Φy(y)−Φy(y′)+Φt(x,y,y′))
  训练过程的cost变为如下。能看出这里分为两部分，加部分和减部分：

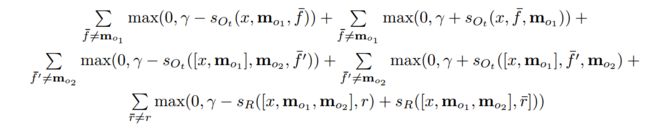
  预测过程的 o1=O1(x,m)=argmaxi=1,...,NsO(x,mi) 用下面算法代替，值大于0意味着 mi 好于 mt ：

  增加这三个维度，使得记忆模型可以知道记忆的相对写入时间，也就知道对话的顺序（order）。当然，如果对话里自身就包括了时间词或者时间状态，则也不一定需要这三个维度。
  4、如果有未登录词汇呢？For example, the first time the word “Boromir” appears in Lord of The Rings。作者把D增加到了5*lenW。
  5、更精确的匹配。作者把D增加到了8*lenW。

代码：

代码来源：https://github.com/npow/MemNN（万分感谢作者）

     https://github.com/wuxiyu/MemNN（我的folk，添加了注释和数据集）

数据集：

  来源于Facebook组织的对话集Toy QA tasks
先看一个训练集的例子：

  1 John travelled to the hallway.
  2 Mary journeyed to the bathroom.
  3 Where is John? hallway 1

  这是一个对话组，句子前面是id。对话组最前面n句是陈述句，用于记忆推论，最后有一句问句，及其答案。答案后面的数字叫做事实（fact），或者叫做支撑记忆（the supporting memories两个词混用），是一个索引，指向支持这个答案回答的那个对话句子。
  最后返回字典的数组。如list：[{‘text’: ‘Mary moved to the bathroom.’, ‘type’: ‘s’}, {‘answer’: ‘bathroom’, ‘text’: ‘Where is Mary’, ‘refs’: [1], ‘type’: ‘q’, ‘id’: 3}]

数据预处理：

  作者调用sklearn的类CountVectorizer进行预处理。
  先是fit传入数据构建模型，然后分别transform返回需要的向量（包括词汇的和句子的），将对话组转化为词频的向量空间模型。在这里，记忆的构建简单处理，每读到一句陈述句，就提取它在VSM里对应的向量，然后将向量插进memory_list记忆数组里，直到遇到了问句就停止。

函数剖析：

def create_train(self, lenW, n_facts):

  这是创建训练模型的函数。传入的包括了事实的数组，问句的id，memory_list（这里模拟了记忆的G过程，简单地将memory（也就是那些陈述句）的向量空间模型，放到这个memory_list数组里。）
  这个函数主要干的是模型O和R部分（正如作者所说的，这个模型主要大头在这两部分上）。
  函数里的m是里一个列表list，list[0]是问句的id，list剩下部分是支撑记忆（支撑记忆其实也是id，所指向的陈述句的id）。作者在这里做了一个小技巧，创建了一个2倍事实数量的数组cost_arr，其中偶数作为公式里的减部分，奇数作为公式里的加部分。当事实数大于一时，由于线性空间加总的缘故，利用scan的迭代，传入前i个事实（代码里是i+1，因为第一个是问句的id，不是事实），最后加总，具体见上面，不赘述。
  代码里有这么一句：

T.switch(T.or_(T.eq(t, f[i]), T.eq(t, T.shape(L)[0]-1)), 0, T.largest(gamma - s_Ot(T.stack(*m[:i+1]), f[i], t, L), 0))

  改成类似的ifelse如下，就好理解多了：

if ( (t == f[i]) ) | (t == T.shape( L )[0] - 1){ 
        return 0
}else{
        return T.largest( gamma - s_Ot( T.stack( *m[: i + 1] ), f[i], t, L ), 0 ) 
}

  函数最后返回的是用于训练的cost函数，具体公式见上文。