《Streaming System》 第二章：数据处理的四要素 What Where When and How

本文由《Streaming System》一书第二章的提炼翻译而来，译者才疏学浅，如有错误，欢迎指正。转载请注明出处，侵权必究。

本章主要介绍鲁棒的处理乱序数据的核心概念，这些概念的运用使流处理系统超越批处理系统的关键所在。

路线图

上一章中，我们介绍了两个非常关键的概念：

• 事件时间和处理时间，只有在事件时间维度对数据进行处理，才能保证计算结果的准确性
• 窗口：窗口是处理无界数据流的通用方法，目前共有4类窗口。
  接下来我们介绍其他三个同样非常重要的概念：
• 触发器（Triggers）
  触发器是决定某个窗口何时输出的一种机制。作用跟照相机的快门相同，按下去，就能拿到某个时间点计算结果的快照。通过触发器，也能多次看到某个窗口的输出结果。因此可以实现迟到数据（late event）的处理。
• Watermark（水印）
  Watermark是描述事件时间上数据完整性的概念。时间点X上的Watermark表示了所有时间点X前的输入数据都到齐了。本节会粗浅的介绍一下watermark，第三章中会对watermark做深入解释。
• Accumulation（累积）
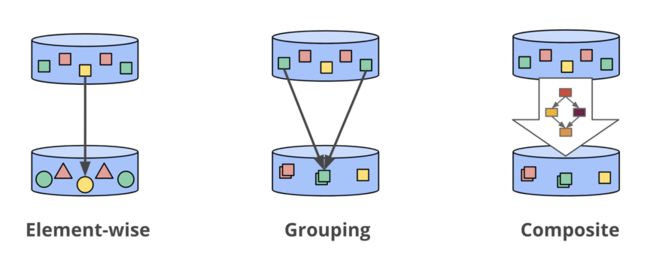
  累积模式表示了同一个窗口不同输出间的关系。这些结果间可能完全无关，比如该窗口不同时间的增量，也可能有重叠。不同的累积模式在语义和成本上都不同，要根据具体场景来选择合适的累积方式。

接下来，我抛出4个在无界数据处理过程中，最为关键的问题：

• 计算什么结果（__What__ results are calculated?）？这是用户在代码（SQL/pipline code）中定义的，比如求和，算直方图或训练机器学习模型等。这也是批处理解决的经典问题。
• 在事件时间的哪个地方计算结果（__Where__ in event time are results calculated）？这是用户在代码中定义的基于事件时间的窗口中定义的。可是使用上一章中介绍的滚窗/划窗/会话等窗口，也可以使用跟窗口无关的算子，或者更复杂的窗口，比如限时拍卖。
• 在什么处理时间点，可以输出结果（__When__ in processing time are results materialized）？触发器和watermark会解决这个问题。这个主题有很多个变种，但是最常见的是重复更新场景（比如，物化视图语义），其使用watermark来指示窗口的输入数据已经完整，看到watermark后，这个窗口才唯一输出一次数据。
• 如何更新结果（__How__ do refinements of results relate）？三种方式可以解决这个问题：discarding，accumulating和accumulating and retracting。下文会对这三种模式做更详细介绍。

批处理的基础：What&Where

咱们先来看一下批处理中如何解决What和Where两个问题。

What: Transformations（变换）

批处理中，用变换（Transformations）解决 “Whatresults are calculated?”这个问题。
接下来用一个实例来说明。假设我们要算一次电子游戏比赛中，某一队的总得分。这个例子的特点：对输入数据，在主键上，进行求和计算。具体数据如下：

各列数据含义：

• Score：队中每个队员得分
• EventTime：队员得分时间
• ProcTime：数据进入系统进行计算的时间
  对数据以EventTime和ProcessTime作图，如下所示：

我们用Beam伪代码来实现这个示例，如果你之前用过Flinkl或Spark，那么代码理解起来应该相对简单。首先介绍一下Beam的基本知识，Beam中有两类基本操作：

• PCollections：可以被并发处理的数据集
• PTransforms：对数据集进行的操作。比如group/aggregate等，读如PCollection并产生新的PCollection。

PCollection raw = IO.read(...);  //读入原始数据
//将原始数据解析成格式划数据，其中Team为String类型，是主键。score是整型。
PCollection> scores =
input.apply(Sum.integersPerKey()); // 在每个主键上，对score做求和操作

我们通过一个时序图来看看以上代码是如何处理这些数据的：

图中，X轴是EventTime，Y轴是Processing Time，黑色的线表示随着时间推移对所有数据进行计算，前三幅图白色的数字（12，30，48）为该processing time时间点上，计算的中间结果，在批处理中，这些中间结果会被保存下来。最后一幅图是指整个计算完整个数据集之后，输出最终结果48。这就是整个经典批处理的处理过程。由于数据是有界的，因此在process time上处理完所有数据后，就能得到正确结果。但是如果数据集是无界数据的话，这样处理就有问题。接下来我们讨论"Where in event time are results calculated?"这个问题。

Where: Windowing

上一章我们讨论了3中常用的窗口：固定窗口（又称为滚动窗口），滑动窗口和会话窗口。窗口将无界数据源沿着临时边界，切分成一个个有界数据块。
以下是用在Beam中，代码中用窗口如何实现之前整数求和的例子：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))) 
  .apply(Sum.integersPerKey());

理论上批数据是流数据的子集，因此Beam在模型层面对批流做了统一。我们通过时序图看一下在传统批处理引擎中，以上代码是如何执行的：

从时序图上可以看出，在事件时间上，以2分钟为步长，将数据切分到不同的窗口。然后每个窗口的输出进行累加就得到最终结果。
以上我们回顾了时间域（事件时间和处理时间的关系）和窗口的相关知识，接下来看一下触发器，watermark和accumulation这三个概念。

Going Streaming: When & How

批处理系统要等到所有数据都到齐才能输出计算结果，在无界数据流计算中是不可行的。因此流计算系统中引入了触发器（triggers）和watermark的概念。

When: The wonderful thing about triggers, is triggers are wonderful things!

触发器解决了‘When in processing time are resultsmaterialized?’这个问题。触发器会根据事件时间上的watermark来决定，在处理时间的哪个时间点来输出窗口数据。每个窗口的输出称为窗口的窗格（pane of the window）。
有两种通用的最基础的trigger类型：

• 重复更新触发器（Repeated update triggers），定期触发窗口输出。比如每条数据都输出一个结果，或者在processing time上每隔一分钟输出一个结果。
• 完整性触发器（Completeness triggers），仅当窗口的数据完整时，才输出窗口结果。跟传统批处理非常类似。只不过窗口的大小不同，传统批处理是要等整个数据集的数据都到齐，才进行计算。
  重复更新触发器是最常用的触发器，因为其易于理解和使用，并且跟数据库中的物化视图语义非常相似。流计算中，完整性触发器的语义跟传统批处理更相似，能够处理late event。Watermark是驱动Completeness Triggers被触发的原语。接下来我们会重点介绍watermark。

我们先看个重复更新触发器的代码示例片段，这个片段实现了每个元素都触发的功能：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
                .triggering(Repeatedly(AfterCount(1))));
  .apply(Sum.integersPerKey());

在流计算系统中，其处理的时序图如下：

数据按事件时间被切分成了2分钟的固定窗口。每个窗口中，每来一条数据，窗口就触发一次计算并输出。当流计算对接的下游系统是MySQL等某个Key的数据可以被更新的话，用户就能得到每个窗口中的最新的计算结果。

每个事件都触发计算的模式不适合在大规模数据量的情况下使用，系统的计算效率会非常低，并且会对下游系统造成很大的写压力。一般情况下，在实际使用过程中，用户通常会在处理时间上定义一个延时，多长时间输出一次（比如每秒/每分钟等）。

触发器中，在处理时间延时上有两种方式：

• 对齐延时：将处理时间上切分成固定大小的时间片，对每个key的每个窗口，时间片大小都相同。
• 非对齐延时：延时时间与窗口内数据有关。
  译者注：简单理解，对齐延时，就是按固定时间来触发计算。而非对齐延时，是按照数据进入系统的时间+延时时间触发计算。

对齐延时的伪代码片段如下：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(Repeatedly(AlignedDelay(TWO_MINUTES)))
  .apply(Sum.integersPerKey());

时序图：

上图表示，Process Time上，每两分钟各个窗口都输出一次数据。Spark streaming中micro-batch就是对齐延时的一种实现。好处是会定期输出结果。缺点是如果数据有负载高峰，在tps很高的时候，系统的负载也会很高。会导致延时。非对齐延时的代码实现如下：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(Repeatedly(UnalignedDelay(TWO_MINUTES))
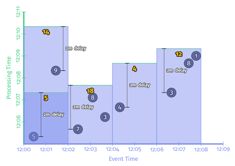
  .apply(Sum.integersPerKey());

时序图如下：

上图中，每个Event Time窗口中，当窗口中有数据时，会在数据的Process Time上，被切成2min大小的数据块。没有数据时，这个窗口是不进行计算的。每个窗口的输出时间是不同的。也就是所谓的每个窗口的输出‘非对齐’模式。这种模式与对齐模式相比的好处是：在每个窗口上，负载更均衡。比如某个event time窗口中出现流量高峰，会立即进行计算输出结果，而不会依赖其他窗口的情况。但最终，两种模式的延时是相同的。

重复更新触发器使用和理解起来非常简单，但不能保证计算结果的正确性，无法处理late event。而Completeness triggers（完整性触发器）能解决这个问题。我们先来了解一下watermark。

When: Watermarks

Watermark标志着在Process Time上，何时应该输出结果。换句话说，watermark是某个event time窗口中所有数据都到齐的标志。一旦窗口的watermark到了，那么这个event time窗口里的数据就到齐了，可以进行计算了。下图是event time和process time的关系。图中的红线就是watermark。Event Time和Process Time的关系可以表示为：F(P)->E，F这个公式就是watermark。

有两种类型的watermark：

• 完美型watermark：完美性watermark指，能够100%保证某个event time X之前的数据都到齐了，不会有late event。
• 启发式watermark：在真实世界无界数据的处理中，无法确切知道某个event timeX之前的数据是否到齐。因此要用到启发式watermark。启发式watermark会根据某些条件推测X之前的数据已经到齐。但推测有可能是错的，有可能会有late event出现。
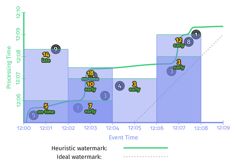
  watermark标志着Event Time窗口中的数据是否完整，是Completeness triggers的基础。下面看个completeness triggers的示例代码：

  PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(AfterWatermark()))
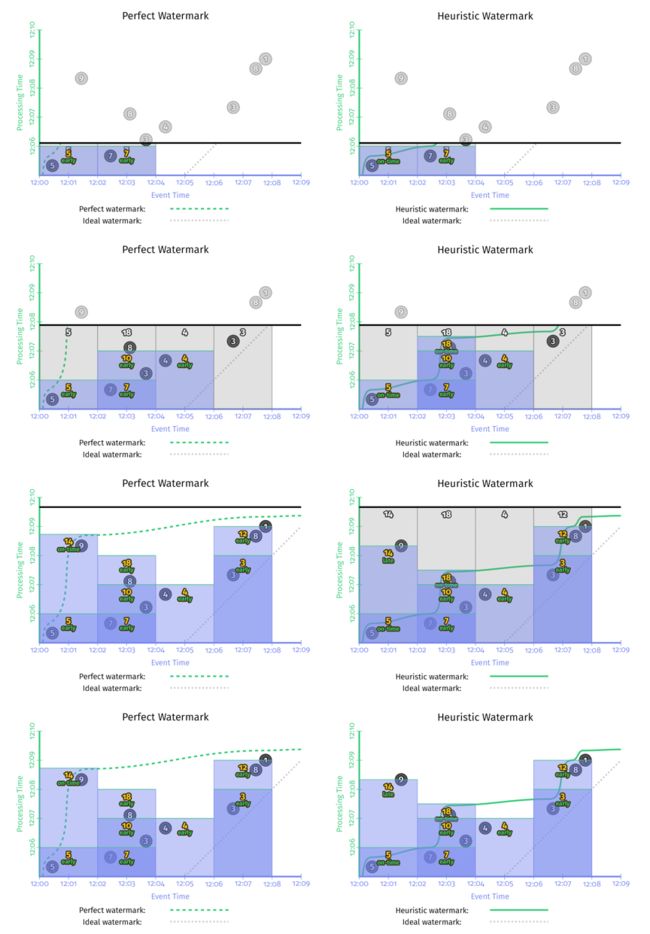
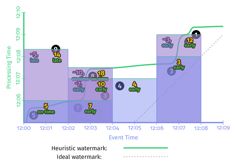
  .apply(Sum.integersPerKey());

我们注意到，代码中watermark是个Function（AfterWatermark）。这个function可以有多种实现方式，比如如果能确切知道数据是否完整，就可以用Prefect Watermark。如果不能，则要使用启发式watermark。下图是在同一个数据集上使用两种不同的watermark的行为，左边是perfect watermark，右边是启发式的watermark。

在以上两种情况中，每次watermark经过event time窗口时，窗口都会输出计算结果。区别是perfect watermark的结果是正确的，但推断型watermark的结果是错误的，少了第一个窗口中‘9’这个数据。

在两个流的outer join场景中，如何判断输入数据是否完整？是否能做join？如果采用在process time上延时的重复更新型触发器进行计算，如果数据在event time有较大延时或者数据有乱序，那么计算结果就错了。在这种场景下，event time上的watermark对处理late event，保证结果正确性，就非常关键了。

当然，没有完美的设计，watermark也有两个明显的缺点：

• 输出太慢：如果数据流中有晚到数据，越趋近于perfect watermark的watermark，将会一直等这个late event，而不会输出结果，这回导致输出的延时增加。如上图左边的一侧所示。在[12:00,12:02)这个窗口的输出，与窗口第一个元素的event time相比，晚了将近7分钟。对延时非常敏感的业务没办法忍受这么长的延时。
• 输出太快：启发式watermark的问题是输出太快，会导致结果不准。比如上图中右边一侧所示，对late event ‘9’，被忽略了。

因此，水印并不能同时保证无界数据处理过程中的低延时和正确性。既然重复更新触发器（Repeated update triggers）可以保证低延时，完整性触发器（Completeness triggers），能保证结果正确。那能不能将两者结合起来呢？

When: early/on-time/late triggers FTW!

上文中，我们介绍了两种触发器：重复更新触发器（Repeated update triggers）和完整性触发器（Completeness triggers），如果将两种触发器的优势结合，即允许在watermark之前/之时/之后使用标准的重复更新触发器。就产生了3种新的触发器：early/on-time/late trigger：

• Zero or more early panes：在watermark经过窗口之前，即周期性的输出结果。这些结果可能是不准的，但是避免了watermark 输出太慢的问题。
• A single on-time pane：仅在watermark通过窗口结束时触发一次。这时的结果可以看作是准确的。
• Zero or more late panes：在watermark通过窗口结束边界之后，如果这个窗口有late event，也可以触发计算。这样就可以随时更新窗口结果，避免了输出太快导致的结果不对的问题。

在本章的例子中，在watermark的基础上，如果加一个1min的early firing trigger和一个每个record都会输出的late firing trigger，那么在event time上2min的窗口，使用1min的early firing trigger每隔一分钟就会输出一次，并且如果有late event，late firing trigger还能纠正之前窗口输出的结果。这样保证了正确性的情况下，还不增加延时。

PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(AfterWatermark()
                             .withEarlyFirings(AlignedDelay(ONE_MINUTE))
                             .withLateFirings(AfterCount(1))))
  .apply(Sum.integersPerKey());

由上如所示，加上了early firing trigger和late firing trigger后，完美型watermark和推断型watermark的结果就一致了。与没有加这两种trigger的实现相比，有了两点很明显的改进：

• 输出太晚（too slow）：在左侧perfect watermark的时序图中，第二个窗口[12:02,12:04)中，如果没有加early firing trigger，第一个数据‘7’发生的时间是12:02, 窗口的输出是12:09，第二个窗口的输出延时了近7分钟。加了early firing trigger之后，窗口第一次输出时间是12:06，提前了3分钟。上图右侧启发式watermark情况也非常类似。
• 输出太早（too fast）：第一个窗口[12:00,12:02)中，启发式窗口的watermark太早，late event ‘9’没有被算进去，加了late firing trigger之后，当'9'进入系统时，会触发窗口的再次计算，更正了之前窗口输出的错误结果，保证了数据的正确性。

完美型watermark和推断型watermark一个非常大的区别是，在完美型watermark例子中，当watermark经过窗口结束边界时，这个窗口里的数据一定是完整的，因此得出该窗口计算结果之后，就可以吧这个窗口的数据全部删除。但启发式watermark中，由于late event的存在，为了保证结果的正确性，需要把窗口的数据保存一段时间。但其实我们根本不知道要把这个窗口的状态保存多长时间。这就引出了一个新的概念：允许延时（allowed lateness）。

When: Allowed Lateness (i.e., Garbage Collection)

为了保证数据正确性，当late event到来后能够更新窗口结果，因此窗口的状态需要被持久化保存下来，但到底应该保存多长时间呢？实际生产环境中，由于磁盘大小等限制，某窗口的状态不可能无限的保存下去。因此，定义窗口状态的保存时间为allowed lateness（允许的延迟）。也就是说，过了这个时间，窗口中数据会被清掉，之后到来的late event就不会被处理了。我们看个带allowed lateness参数的例子：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(
                 AfterWatermark()
                   .withEarlyFirings(AlignedDelay(ONE_MINUTE))
                   .withLateFirings(AfterCount(1)))
               .withAllowedLateness(ONE_MINUTE)) 
 .apply(Sum.integersPerKey());

时序图如下：

关于allowed lateness的两个重点：

1. 如果数能够使用perfect watermark，即有序，则不需要考虑allowed lateness的问题
2. 如果是对有限个key做全局聚合，则不必考虑allowed lateness问题。（因为部分全局聚合比如sum/agg等，可以做增量计算，不必要保存所有数据）

How: Accumulation

如果遇到late event，要如何修改窗口之前输出的结果呢？有三种方式：

• Discarding（抛弃）：每个窗口产生输出之后，其state都被丢弃。也就是各个窗口之间完全独立。比较适合下游是聚合类的运算，比如对整数求和。
• Accumulating（累积）：所有窗口的历史状态都会被保存，每次late event到了之后，都会触发重新计算，更新之前计算结果。这种方式适合下游是可更新的数据存储，比如HBase/带主键的RDS table等。

• Accumulating & Retracting（累积&撤回）：Accumulating与第二点一样，即保存窗口的所有历史状态。撤回是指，late event到来之后，出了触发重新计算之外，还会把之前窗口的输出撤回。以下两个case非常适合用这种方式：

  • 如果窗口下游是分组逻辑，并且分组的key已经变了，那late event的最新数据下去之后，不能保证跟之前的数据在同一个分组，因此，需要撤回之前的结果。
  • 动态窗口中，由于窗口合并，很难知道窗口之前emit的老数据落在了下游哪些窗口中。因此需要撤回之前的结果。
    以例子中第二个窗口[12:02,12:04)为例，我们分别看看三种模式的输出结果：

	Discarding	Accumulating	Accumulating& Retracting
Pane 1: inputs=[7,3]	10	10	10
Pane 2: inputs=[8]	8	18	18, -10
Last NormalValue	8	18	18
Total Sum	18	28	18

• Discarding（抛弃）：同一个窗口的每次输出，都与之前的输出完全独立。本例子中，要算求和的话，只需要把窗口的每次输出都加起来即可。因此Discarding 模式对下游是聚合（SUM/AGG）等场景非常何时。
• Accumulating（累积）：窗口的会把之前所有state都保存，因此同一个窗口的每个输出，都是之前所有数据的累积值。本例子中，该窗口第一次输出是10，第二次输入是8，之前的状态是10，所以输出是18。如果下游计算直接把两次输出加起来，结果就是错的。
• Accumulating & Retracting（累积&撤回）：窗口的每个输出，都有一个累积值和一个撤回值。本例中，第一次输出10，第二次输出的是[18,-10]，因此下游把窗口的所有输出求和，会减去之前的重复值，得到正确结果18.
  Discarding 模式的代码示例如下：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(
                 AfterWatermark()
                   .withEarlyFirings(AlignedDelay(ONE_MINUTE))
                   .withLateFirings(AtCount(1)))
               .discardingFiredPanes())
  .apply(Sum.integersPerKey());

使用启发式水印，在流计算引擎中，上述代码对应的时序图如下：

Accumulating&Retraction示例代码：

 PCollection> scores = input
  .apply(Window.into(FixedWindows.of(TWO_MINUTES))
               .triggering(
                 AfterWatermark()
                   .withEarlyFirings(AlignedDelay(ONE_MINUTE))
                   .withLateFirings(AtCount(1)))
               .accumulatingAndRetractingFiredPanes())
  .apply(Sum.integersPerKey());

时序图如下：

三种模式时序图放在一起比较如下：

三个图从左到右分别为discarding，accumulation，accumulation&retraction三种模式的时序图。在计算消耗（单作业使用的资源）和存储消耗上，从左到右依次增加。

总结

总结以下本文主要讲的概念：

• Event time vs processing time（事件时间 vs. 处理时间）
• 窗口
• 触发器
• Watermarks
• Accumulation
  本文主要解决的四个问题：
• What results are calculated? = transformations.
• Where in event time are results calculated? = windowing.
• When in processing time are results materialized? = triggers + watermarks.
• How do refinements of results relate? = accumulation.

流计算的本质，就是平衡正确性，延时和资源这三者的关系。

 

	整数求和 Example 2-1 /Figure 2-3	整数求和 Fixed windowsbatch Example 2-2 /Figure 2-5	整数求和 Fixed windowsstreaming Repeated per-record trigger Example 2-3 /Figure 2-6
	整数求和 Fixed windowsstreaming Repeatedaligned-delaytrigger Example 2-4 /Figure 2-7	整数求和 Fixed windowsstreaming Repeatedunaligned-delaytrigger Example 2-5 /Figure 2-8	整数求和 Fixed windowsstreaming Heuristicwatermarktrigger Example 2-6 /Example 2-6
	整数求和 Fixed windowsstreaming Early/on-time/late trigger Discarding Example 2-10 /Figure 2-13	整数求和 Fixed windowsstreaming Early/on-time/late trigger Accumulating Example 2-7 /Figure 2-11	整数求和 Fixed windowsstreaming Early/on-time/late trigger Accumulating& Retracting Table 2-11 / Figure 2-14

 

本章中，仅介绍了部分固定窗口的内容，下一章的主要内容是watermark。介绍完watermark后，我们会深入研究其他两种类型的窗口。

转载自：https://developer.aliyun.com/article/674450?spm=a2c6h.13262185.0.0.29158a3bxTGD5K