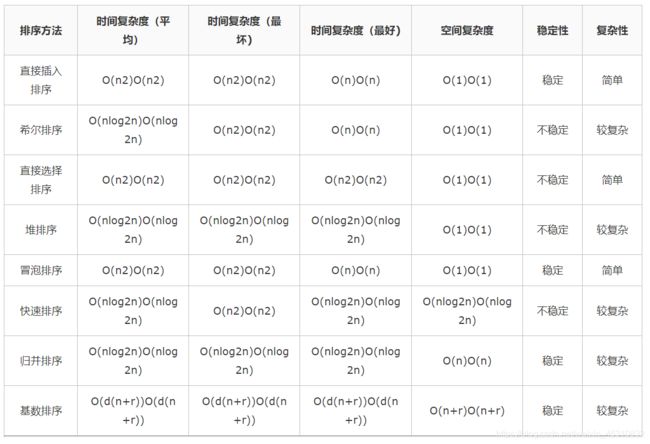
十大排序的Java实现以及横向对比、时间复杂度
标题
-
- 一、冒泡排序
- 二、选择排序
- 三、插入排序
- 四、希尔排序
- 五、归并排序
- 六、快速排序
- 七、堆排序
- 八、计数排序
- 九、桶排序
- 十、基数排序
- 十大排序的时间复杂度与空间复杂度对比
一、冒泡排序
两两比较,大的靠后
public class BubbleSorting {
public static void main(String[] args) {
int[] numbers=new int[]{1,5,8,2,3,9,4};
int i,j;
for(i=0;inumbers[j+1])
{
int temp=numbers[j];
numbers[j]=numbers[j+1];
numbers[j+1]=temp;
}
}
}
System.out.println("从小到大排序后的结果是:");
for(i=0;i 总结:冒泡排序结果稳定,但时间长,如果排序的数据量大不建议用冒泡排序。
二、选择排序
第一轮:先选出最小的元素放在首位;
第二轮:除了第一轮确定的最小元素,其他元素继续选最小的放在第一轮最小的后面;
…
以此类推,直至最后一轮选择结束,排序完成
public class SelectionSort {
public static void main(String[] args) {
int[] arr={1,3,2,45,65,33,12};
System.out.println("交换之前:");
for(int num:arr){
System.out.print(num+" ");
}
//选择排序的优化
for(int i = 0; i < arr.length - 1; i++) {// 做第i趟排序
int k = i;
for(int j = k + 1; j < arr.length; j++){// 选最小的记录
if(arr[j] < arr[k]){
k = j; //记下目前找到的最小值所在的位置
}
}
//在内层循环结束,也就是找到本轮循环的最小的数以后,再进行交换
if(i != k){ //交换a[i]和a[k]
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
System.out.println();
System.out.println("交换后:");
for(int num:arr){
System.out.print(num+" ");
}
}
}
总结:所需时间和冒泡时间一样,但结果不稳定。
三、插入排序
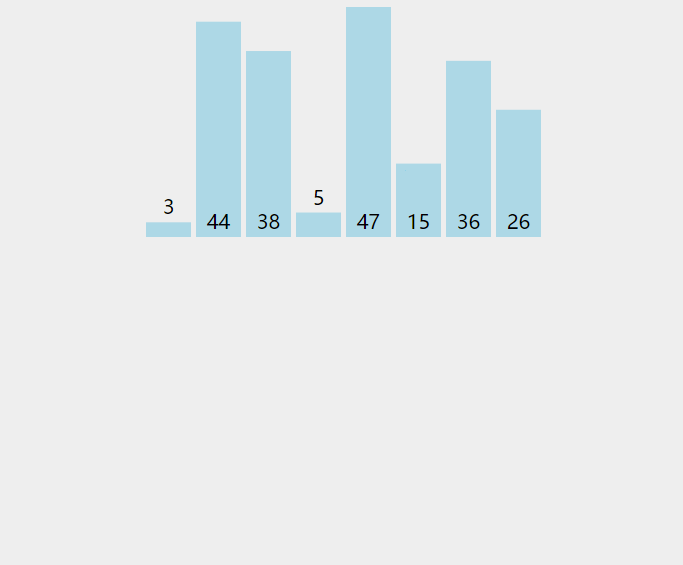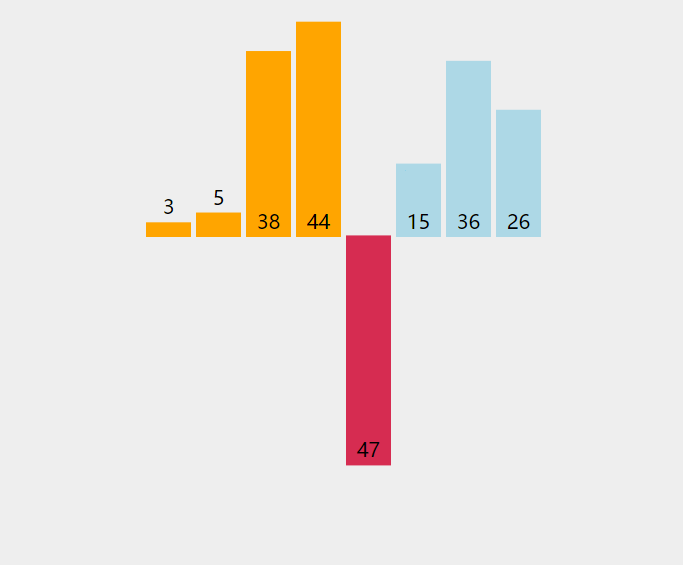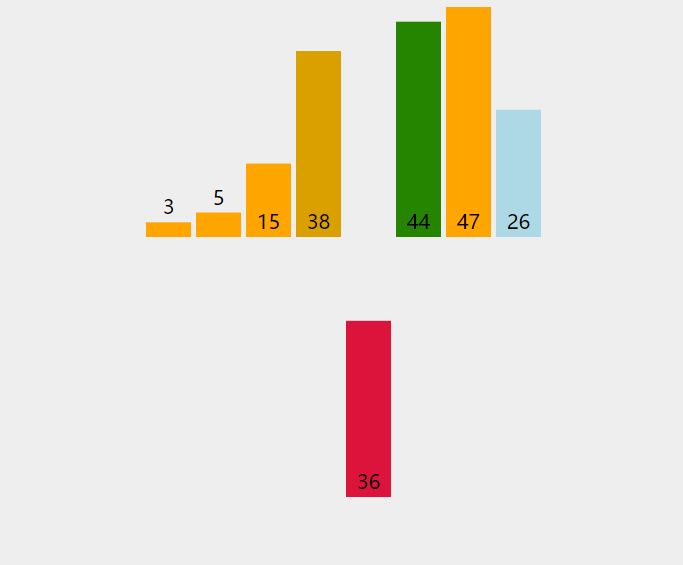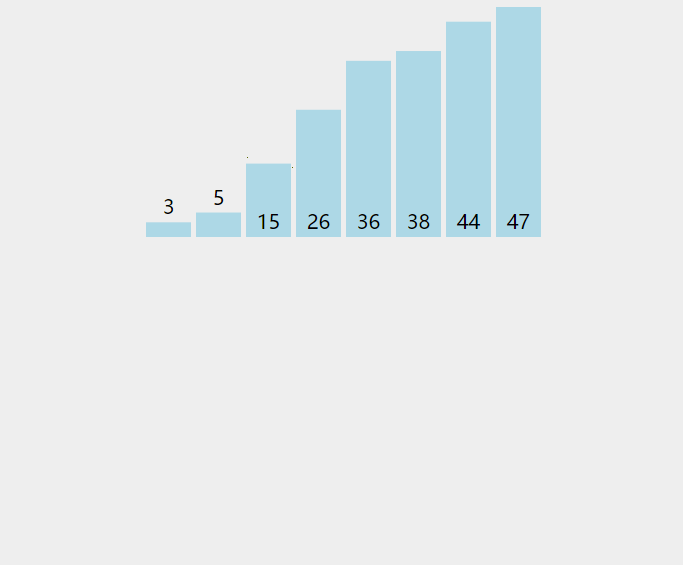
将一个记录插入到已排好序的序列中,从而得到一个新的有序序列(将序列的第一个数据看成是一个有序的子序列,然后从第二个记录逐个向该有序的子序列进行有序的插入,直至整个序列有序)
动图演示如下:
public class inserSort {
public static void main(String args[]) {
int[] array = {4, 2, 7, 3, 5, 4, 0, 45, 16, 36};
for (int i = 1; i < array.length; i++) { //默认第零个是有序的
for (int j = i; j > 0; j--) { //每次从右边组增加一个数,与左边数据判断,交换位置(左边数据进行排序)
if (array[j] < array[j - 1]) {
int temp = array[j];
array[j] = array[j - 1];
array[j - 1] = temp;
}
}
}
for (int n = 0; n < array.length; n++) {
System.out.println(array[n]);
}
}
}
总结:时间复杂度均相同,结果稳定。
四、希尔排序
理解博客:希尔排序
动图演示:
public class ShellSort {
public static void main(String args[]){
int[] arr = {5, 1, 7, 3, 1, 6, 9, 4};
shellSort(arr);
for (int i : arr) {
System.out.print(i + "\t");
}
}
private static void shellSort(int[] arr) {
for (int step = arr.length / 2; step > 0; step /= 2) {
//对一个步长区间进行比较 [step,arr.length)
for (int i = step; i < arr.length; i++) {
int value = arr[i];
int j;
//对步长区间中具体的元素进行比较
for (j = i - step; j >= 0 && arr[j] > value; j -= step) {
//j为左区间的取值,j+step为右区间与左区间的对应值。
arr[j + step] = arr[j];
}
//此时step为一个负数,[j + step]为左区间上的初始交换值
arr[j + step] = value;
}
}
}
}
总结:时间较短,结果不稳定。
五、归并排序
①把 n 个记录看成 n 个长度为1的有序子表;
②进行两两归并使记录关键字有序,得到 n/2 个长度为 2 的有序子表;
③重复第②步直到所有记录归并成一个长度为 n 的有序表为止。
动图演示:
![]()
public class myMergeSor {
static int number=0;
public static void main(String[] args) {
int[] a = {26, 5, 98, 108, 28, 99, 100, 56, 34, 1 };
printArray("排序前:",a);
MergeSort(a);
printArray("排序后:",a);
}
private static void printArray(String pre,int[] a) {
System.out.print(pre+"\n");
for(int i=0;i=right)
return;
int mid = (left + right) / 2;
//二路归并排序里面有两个Sort,多路归并排序里面写多个Sort就可以了
Sort(a, left, mid);
Sort(a, mid + 1, right);
merge(a, left, mid, right);
}
private static void merge(int[] a, int left, int mid, int right) {
int[] tmp = new int[a.length];
int r1 = mid + 1;
int tIndex = left;
int cIndex=left;
// 逐个归并
while(left <=mid && r1 <= right) {
if (a[left] <= a[r1])
tmp[tIndex++] = a[left++];
else
tmp[tIndex++] = a[r1++];
}
// 将左边剩余的归并
while (left <=mid) {
tmp[tIndex++] = a[left++];
}
// 将右边剩余的归并
while ( r1 <= right ) {
tmp[tIndex++] = a[r1++];
}
System.out.println("第"+(++number)+"趟排序:\t");
// TODO Auto-generated method stub
//从临时数组拷贝到原数组
while(cIndex<=right){
a[cIndex]=tmp[cIndex];
//输出中间归并排序结果
System.out.print(a[cIndex]+"\t");
cIndex++;
}
System.out.println();
}
}
总结:时间短,结果稳定,但需要额外的内存空间。
六、快速排序
利用分治法来对待排序序列进行分治排序,它的思想主要是通过一趟排序将待排记录分隔成独立的两部分,其中的一部分比关键字小,后面一部分比关键字大,然后再对这前后的两部分分别采用这种方式进行排序,通过递归的运算最终达到整个序列有序,下面我们简单进行阐述。
动图演示:
![]()
public class quickSort {
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
}
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i=arr[i]&&i 总结:时间短,结果不稳定,不需要额外空间。
七、堆排序
将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
动图演示:
public class heapSort {
public static void main(String[] args) {
int[] arr = {16, 7, 3, 20, 17, 8};
heapSort(arr);
for (int i : arr) {
System.out.print(i + " ");
}
}
//创建堆
private static void heapSort(int[] arr) {
//创建堆
for (int i = (arr.length - 1) / 2; i >= 0; i--) {
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr, i, arr.length);
}
//调整堆结构+交换堆顶元素与末尾元素
for (int i = arr.length - 1; i > 0; i--) {
//将堆顶元素与末尾元素进行交换
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//重新对堆进行调整
adjustHeap(arr, 0, i);
}
}
private static void adjustHeap(int[] arr, int parent, int length) {
//将temp作为父节点
int temp = arr[parent];
//左孩子
int lChild = 2 * parent + 1;
while (lChild < length) {
//右孩子
int rChild = lChild + 1;
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (rChild < length && arr[lChild] < arr[rChild]) {
lChild++;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= arr[lChild]) {
break;
}
// 把孩子结点的值赋给父结点
arr[parent] = arr[lChild];
//选取孩子结点的左孩子结点,继续向下筛选
parent = lChild;
lChild = 2 * lChild + 1;
}
arr[parent] = temp;
}
}
总结:时间复杂度固定不变,结果不稳定,不需要额外空间。
八、计数排序
新建一个长度为n-m+1的临时数组
遍历待排序数组,它的值-m作为临时数组下角标,这个位置的值加1
遍历结束,临时数组就存储了每个值得个数
最后将它展开赋值给原数组
动图演示:
![]()
public class countSort {
public static void main(String[] args) {
//测试
int[] arr = {1,4,6,7,5,4,3,2,1,4,5,10,9,10,3};
sortCount(arr, 1, 10);
System.out.println(Arrays.toString(arr));
}
//计数排序的初步实现,使用了多余的空间,可以尝试不使用多余的空间
public static void sortCount(int[] arr, int m, int n) {
int len = arr.length;
int[] tem = new int[n - m + 1];
for(int i = 0; i < len; i++) {
tem[arr[i] - m] += 1;
}
for(int i = 0, index = 0; i < tem.length; i++) {
int item = tem[i];
while(item-- != 0) {
arr[index++] = i + m;
}
}
}
}
总结:时间复杂度不变,结果稳定,需要额外空间。
九、桶排序
public class bucketSort {
public static void main(String[] args) {
// 输入元素均在 [0, 10) 这个区间内
float[] arr = new float[] { 0.12f, 2.2f, 8.8f, 7.6f, 7.2f, 6.3f, 9.0f, 1.6f, 5.6f, 2.4f };
bucketSort(arr);
printArray(arr);
}
public static void bucketSort(float[] arr) {
// 新建一个桶的集合
ArrayList> buckets = new ArrayList>();
for (int i = 0; i < 10; i++) {
// 新建一个桶,并将其添加到桶的集合中去。
// 由于桶内元素会频繁的插入,所以选择 LinkedList 作为桶的数据结构
buckets.add(new LinkedList());
}
// 将输入数据全部放入桶中并完成排序
for (float data : arr) {
int index = getBucketIndex(data);
insertSort(buckets.get(index), data);
}
// 将桶中元素全部取出来并放入 arr 中输出
int index = 0;
for (LinkedList bucket : buckets) {
for (Float data : bucket) {
arr[index++] = data;
}
}
}
/**
* 计算得到输入元素应该放到哪个桶内
*/
public static int getBucketIndex(float data) {
// 这里例子写的比较简单,仅使用浮点数的整数部分作为其桶的索引值
// 实际开发中需要根据场景具体设计
return (int) data;
}
/**
* 我们选择插入排序作为桶内元素排序的方法 每当有一个新元素到来时,我们都调用该方法将其插入到恰当的位置
*/
public static void insertSort(List bucket, float data) {
ListIterator it = bucket.listIterator();
boolean insertFlag = true;
while (it.hasNext()) {
if (data <= it.next()) {
it.previous(); // 把迭代器的位置偏移回上一个位置
it.add(data); // 把数据插入到迭代器的当前位置
insertFlag = false;
break;
}
}
if (insertFlag) {
bucket.add(data); // 否则把数据插入到链表末端
}
}
public static void printArray(float[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ", ");
}
System.out.println();
}
}
总结:时间最长需要O(n²),最短O(n + k),需要额外空间,结果稳定。
十、基数排序
理解:基数排序
动图演示:
![]()
public class radixSort {
private static void radixSort(int[] array,int d)
{
int n=1;//代表位数对应的数:1,10,100...
int k=0;//保存每一位排序后的结果用于下一位的排序输入
int length=array.length;
int[][] bucket=new int[10][length];//排序桶用于保存每次排序后的结果,这一位上排序结果相同的数字放在同一个桶里
int[] order=new int[length];//用于保存每个桶里有多少个数字
while(n总结:时间复杂度不变,结果稳定,需要额外空间。