python矩阵距离计算

源代码：July在线数据分析班第一讲大林老师讲解python运算速度时，曾举例到一矩阵计算速度的例子，不是python的运算速度慢，而是跟选取的方法有关，如都说C 比python快，但是用python多线程与C的单线程比，肯定是python快。
说矩阵计算的例子：正好工作中用到距离计算，试了下果然好用：

课程源代码：官网可去：https://www.julyedu.com/查询课程资料
例子代码求得距离方法，结果开个根号就是；

import numpy as np
import numpy.linalg as la
import time

X = np.array([range(0, 500), range(500, 1000)])
m, n = X.shape
print(m, n)#2行，500列矩阵

'''
D(i, j) = ||xi - xj||^2
'''
t = time.time()
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        D[i, j] = la.norm(X[:, i] - X[:, j]) ** 2
        D[j, i] = D[i, j]
print(time.time() - t)

'''
|xi - xi| = sqrt((xi - xj) * (xi - xj).T)
D(i, j) = (xi - xj) * (xi - xj).T
'''
t = time.time()
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        d = X[:, i] - X[:, j]
        D[i, j] = np.dot(d, d)
        D[j, i] = D[i, j]
print(time.time() - t)

'''
D(i, j) = (xi - xj) * (xi - xj).T
        = xi * xi.T - xi * xj.T - xj * xi.T + xj * xj.T
        = xi * xi.T - 2 * xi * xj.T + xj * xj.T
G(i,j) = xi.T * xj
'''
t = time.time()
G = np.dot(X.T, X)
D = np.zeros([n, n])
for i in range(n):
    for j in range(i + 1, n):
        D[i, j] = G[i, i] - G[i, j] * 2 + G[j,j]
        D[j, i] = D[i, j]
print(time.time() - t)

'''
H(i, j) = G(i, i)
K(i, j) = G(j, j) = H(i, j).T
D(i, j) = H(i, j) + K(i, j) - 2 * G(i, j)
'''
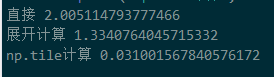
t = time.time()
G = np.dot(X.T, X)
H = np.tile(np.diag(G), (n, 1)) # n rows, 1 for each row
D = H + H.T - G * 2
print(time.time() - t)