loj #2564. 「SDOI2018」原题识别

链接：https://loj.ac/problem/2564
肝了大半天这题。。
总算是肝出来了
第一问首先可以用莫队莽过去。。
那么问题就是第二问了
第二问的话，先考虑链怎么做？
显然，链的话就退化为一个序列了
记录一下每个点，上一个点颜色和他相同的位置就可以记录答案了
距离来说，询问的是(x,y)
那么一个点now，设他上一个颜色一样的位置是z（上一个指的是祖先，如果没有就是0）
如果now是x,y的祖先
那么可以得到他对答案的贡献是$(dep[now]-dep[z])(dep[x]-dep[now]+dep[y]-dep[now]$
拆开式子就可以维护了
否则，now就是y的祖先，且是x的儿子
这个的贡献也用一样的方法讨论就好了
开一个主席树，发现维护下面这些值就够了(其中$xx$是$dep[now]-dep[x]$)

个数 xx的和 $2\ast xx\ast dep[now]$的和 dep[z]的和 dep[now]的和 $dep[now]\ast dep[z]$的和

主席树维护的是每个点到根的信息
写一个函数，calc表示(x,y)这条链的答案，那么就成功了一大半了
考虑扩展到一半的树上
假如我们把那p个点看做主链，我们会发现，每个点到链的距离期望是log的
注意是到主链的距离
一开始我直接当做到LCA的距离，然后发现最后一个点跑了60秒
那么一个询问可以没拆成若干个部分:
1.$[xx,x),[yy,x)$
2.$[xx,x),[x,1]$
3.$[x,1],[yy,1]$
具体定义如下图

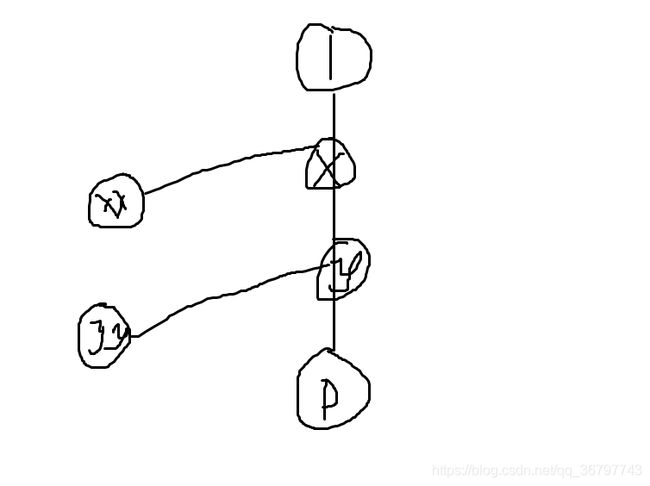
可以发现，后两个部分都是链，可以直接用calc解决
至于第一部分
我们可以暴力枚举$[xx,x)$里面的每一个点，因为期望只有log个
容易发现，只要一个一个点走，就可以维护答案，这里细节较多。。建议准备好对拍
维护答案最大的问题在于，两条链重复的颜色怎么去掉
我们强行算主链的，然后新加的算贡献
利用颜色一样，他们上一个一样的颜色祖先是一样来做，就可以知道主链选什么的时候这个点会有贡献了
要特判0的情况。。因为都是0不一定颜色相同
具体怎么写这里就难得写了

当然，还有和主链不相交的
那么就是到LCA的期望距离为log
暴力枚举两边的点就好了
同样，一个一个算下来就可以维护答案了
因为这里有用的点是log个的，所以直接开一个桶就好了

感觉代码虽然很长，但是思路还是很清晰：
建议结合代码食用

#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int,int> PI;
typedef long long LL;
const int N=200005;
const int MAX=(1<<28);
const int SIZ=440;
struct qq
{
     
	int x,y,last;
}e[N];int num,last[N];
void addedge (int x,int y)
{
     
//	printf("link:%d %d\n",x,y);
	e[++num].x=x;e[num].y=y;
	e[num].last=last[x];
	last[x]=num;
}
int T;
int n,p,m;
int a[N];
unsigned int SA, SB, SC;
unsigned int rng61(){
     SA ^= SA << 16;SA ^= SA >> 5;SA ^= SA << 1;unsigned int t = SA;SA = SB;SB = SC;SC ^= t ^ SA;return SC;}
void gen(){
     scanf("%d%d%u%u%u", &n, &p, &SA, &SB, &SC);for(int i = 2; i <= p; i++)addedge(i - 1, i);for(int i = p + 1; i <= n; i++)addedge(rng61() % (i - 1) + 1, i);for(int i = 1; i <= n; i++) a[i] = rng61() % n + 1;}
int L[N],R[N],id[N];
int fa[N][21],dep[N];
int lst[N];//每个点上一个和他一样的颜色
int g[N],mx;
void dfs (int x)
{
     
	mx=max(mx,dep[x]);
	lst[x]=g[a[x]];int Lst=g[a[x]];g[a[x]]=dep[x];
	L[x]=++num;id[num]=x;
	for (int u=1;u<=20;u++) fa[x][u]=fa[fa[x][u-1]][u-1];
	for (int u=last[x];u!=-1;u=e[u].last)
	{
     
		int y=e[u].y;
		fa[y][0]=x;dep[y]=dep[x]+1;dfs(y);
	}
	num++;R[x]=num;id[num]=x;g[a[x]]=Lst;
}
int get_LCA (int x,int y)
{
     
	if (dep[x]<dep[y]) swap(x,y);
	for (int u=20;u>=0;u--)
		if (dep[fa[x][u]]>=dep[y])
			x=fa[x][u];
	if (x==y) return x;
	for (int u=20;u>=0;u--)
		if (fa[x][u]!=fa[y][u])
			{
     x=fa[x][u];y=fa[y][u];}
	return fa[x][0];
}
LL ans[N];
struct qt
{
     
	int l,r;
	int id,LCA;
}h[N*2];int tot=0;
bool cmp (qt x,qt y)	{
     return x.l/SIZ==y.l/SIZ?x.r<y.r:x.l<y.l;}
bool in[N];
int TOT[N];
LL Ans;
void modify (int x)
{
     
	if (in[x]==true)
	{
     
		TOT[a[x]]--;
		if (TOT[a[x]]==0)  Ans--;
	}
	else
	{
     
		if (TOT[a[x]]==0) Ans++;
		TOT[a[x]]++;
	}
	in[x]^=1;
}
void case1 ()
{
     
	memset(in,false,sizeof(in));
	Ans=0;
	sort(h+1,h+1+tot,cmp);
	int L=1,R=0;
	for (int u=1;u<=tot;u++)
	{
     
		while (R<h[u].r)	modify(id[++R]);
		while (L>h[u].l)	modify(id[--L]);
		while (R>h[u].r) 	modify(id[R--]);
		while (L<h[u].l)	modify(id[L++]);
		if (h[u].LCA) modify(h[u].LCA);
		ans[h[u].id]=Ans;
		if (h[u].LCA) modify(h[u].LCA);
	}
}
struct qy
{
     
	LL c,c1,c2,c3,c4,c5,c6;
	//个数  xx的和    2*xx*dep[now]的和   dep[z]的和   dep[now]的和  dep[now]*dep[z]的和 
	qy () {
     };
	qy(LL _c,LL _c1,LL _c2,LL _c3,LL _c4,LL _c5,LL _c6)	{
     c=_c;c1=_c1;c2=_c2;c3=_c3;c4=_c4;c5=_c5;c6=_c6;}
	void print()
	{
     
		printf("c:%lld c1:%lld c2:%lld c3:%lld c4:%lld c5:%lld c6:%lld\n",c,c1,c2,c3,c4,c5,c6);
	}
};
qy zero;
qy operator + (qy x,qy y)	{
     return qy(x.c+y.c,x.c1+y.c1,x.c2+y.c2,x.c3+y.c3,x.c4+y.c4,x.c5+y.c5,x.c6+y.c6);}
qy operator - (qy x,qy y)	{
     return qy(x.c-y.c,x.c1-y.c1,x.c2-y.c2,x.c3-y.c3,x.c4-y.c4,x.c5-y.c5,x.c6+y.c6);}
int rt[N],num1;
qy c[N*20];
int s1[N*20],s2[N*20];
void change (int &now,int l,int r,int x,qy cc)
{
     
	num1++;c[num1]=c[now];s1[num1]=s1[now];s2[num1]=s2[now];now=num1;
	c[now]=c[now]+cc;
	if (l==r)	
	{
     
		if (c[now].c6==0) c[now].c6=cc.c6;
		else c[now].c6=min(c[now].c6,cc.c6);
		return ;
	}
	int mid=(l+r)>>1;
	if (x<=mid) change(s1[now],l,mid,x,cc);
	else change(s2[now],mid+1,r,x,cc);
}
void dfs2 (int x)
{
     
	int xx=dep[x]-dep[lst[x]];
	qy cc=qy(1LL,(LL)xx,(LL)2*xx*dep[x],(LL)dep[lst[x]],(LL)dep[x],(LL)dep[x]*dep[lst[x]],(LL)dep[x]);
	change(rt[x],0,mx,dep[lst[x]],cc);
	for (int u=last[x];u!=-1;u=e[u].last)
	{
     
		int y=e[u].y;
		rt[y]=rt[x];dfs2(y);
	}
}
qy ask (int rt1,int rt2,int l,int r,int L,int R)
{
     
	if (rt2==0) return zero;
	if (l==L&&r==R)	return c[rt2]-c[rt1];
	int mid=(l+r)>>1;
	if (R<=mid) return ask(s1[rt1],s1[rt2],l,mid,L,R);
	else if (L>mid) return ask(s2[rt1],s2[rt2],mid+1,r,L,R);
	else return ask(s1[rt1],s1[rt2],l,mid,L,mid)+ask(s2[rt1],s2[rt2],mid+1,r,mid+1,R);
}
//个数  xx的和    2*xx*dep[now]的和   dep[z]的和   dep[now]的和  dep[now]*dep[z]的和 
LL calc (int x,int y)//x和y在一条链上  x是LCA 
{
     
	if (x==0) return 0;
	if (dep[x]>dep[y]) swap(x,y);
	LL lalal=0;
	qy d;
	d=c[rt[x]];
	lalal=lalal+d.c1*(dep[x]+dep[y]+2);
	lalal=lalal-d.c2;
	lalal-=d.c;
	d=ask(rt[x],rt[y],0,mx,0,dep[x]-1);
	lalal=lalal+d.c*dep[x]*(dep[y]+1);
	lalal=lalal-d.c3*(dep[y]+1);
	lalal=lalal-d.c4*dep[x];
	lalal=lalal+d.c5;
	return lalal;
}
void add (int x,int c)
{
     
	if (c==1)
	{
     
		if (TOT[x]==0) Ans++;
		TOT[x]++;
	}
	else
	{
     
		TOT[x]--;
		if (TOT[x]==0) Ans--;
	}
}
int vec[N],vec1[N];
int siz,siz1;
vector<int> t[N];
int f[N];
LL case2 (int x,int y,int LCA)
{
     
	if (LCA==x)	return calc(x,y);
	if (LCA>p)//不在主链上 
	{
     
		LL lalal=0;
		lalal=calc(LCA,x)+calc(LCA,y)-calc(LCA,LCA);
		siz=siz1=0;
		while (x!=LCA)	{
     vec[++siz]=x;;x=fa[x][0];}
		while (y!=LCA)	{
     vec1[++siz1]=y;y=fa[y][0];}
		TOT[a[LCA]]++;
		for (int u=siz;u>=1;u--)
		{
     
			Ans=1;
			for (int i=siz;i>=u;i--)	add(a[vec[i]],1);
			for (int i=siz1;i>=1;i--)
			{
     
				add(a[vec1[i]],1);
				lalal=lalal+Ans;
			}
			for (int i=siz;i>=u;i--)	add(a[vec[i]],-1);
			for (int i=siz1;i>=1;i--)	add(a[vec1[i]],-1);
		}
		TOT[a[LCA]]--;
		return lalal;
	}
	else//在主链上 
	{
     
		siz=0;
		int xx=x,yy=y;
		while (x>p)	x=fa[x][0];
		while (y>p)	y=fa[y][0];
		if (x>y)		swap(xx,yy);
		x=xx;y=yy;
		while (x>p)	{
     vec[++siz]=x;x=fa[x][0];}
		while (y>p)	{
     f[a[y]]=dep[y];y=fa[y][0];}
		LL lalal=0;
	//	printf("%d %d %d\n",x,xx,yy);
		lalal=calc(x,yy)+calc(x,xx)-calc(x,x);
	//	printf("lalal:%lld %lld %lld %lld\n",calc(x,yy),calc(x,xx),calc(x,x),lalal);
		LL now;
		now=(calc(x,yy)-calc(fa[x][0],yy))-(calc(x,x)-calc(fa[x][0],x));
		//printf("%lld\n",now);
		for (int u=siz;u>=1;u--)//开始往前移动 
		{
     
			if (lst[vec[u]]==0)
			{
     
				int o=-1;
				int siz2=t[a[vec[u]]].size();
				for (int i=0;i<siz2;i++)
					if (t[a[vec[u]]][i]>x)
						{
     o=t[a[vec[u]]][i];break;}
				if (o>y) o=-1;
			//	printf("o:%d\n",o);
				if (o!=-1) now=now+(dep[o]-dep[x]-1);
				else if (f[a[vec[u]]]!=-1) now=now+(f[a[vec[u]]]-dep[x]-1);
				else now=now+dep[yy]-dep[x];
			}
			else if (lst[vec[u]]<dep[x])
			{
     
				qy cc=ask(0,rt[yy],0,mx,lst[vec[u]],lst[vec[u]]);
				//cc.print();
				if (cc.c==0)//如果没有 
					now=now+(dep[yy]-dep[x]);
				else	now=now+(cc.c6-(dep[x]+1));
			}
			lalal=lalal+now;
		}
		y=yy;while (y>p)	{
     f[a[y]]=-1;y=fa[y][0];}
		return lalal;
	}
}
int main()
{
     
//	freopen("old-task3.in","r",stdin);
	//freopen("a.out","w",stdout);
	c[0]=zero=qy(0,0,0,0,0,0,0);
	scanf("%d",&T);
	while (T--)
	{
     
		memset(g,0,sizeof(g));
		memset(TOT,0,sizeof(TOT));
		num1=mx=0;
		memset(f,-1,sizeof(f));
		tot=num=0;memset(last,-1,sizeof(last));
		gen();
		for (int u=1;u<=n;u++) t[u].clear();
		dep[0]=0;dep[1]=1;num=0;dfs(1);
		for (int u=1;u<=p;u++)	if (lst[u]==0) 
		{
     
			t[a[u]].push_back(u);
		}
		rt[1]=1;s1[1]=0;s2[1]=0;c[1]=zero;
		dfs2(1);
		/*for (int u=1;u<=n;u++) printf("%d ",a[u]);
		printf("\n");*/
		//for (int u=1;u<=n;u++) printf("%d ",lst[u]);printf("\n");
		/*for (int u=1;u<=n;u++) printf("%d %d\n",L[u],R[u]);
		printf("\n");
		for (int u=1;u<=num;u++) printf("%d ",id[u]);
		printf("\n");*/
		scanf("%d",&m);
		for (int u=1;u<=m;u++)
		{
     
			ans[u]=0;
			int op,x,y;
			scanf("%d%d%d",&op,&x,&y);
			if (L[x]>L[y]) swap(x,y);
			int LCA=get_LCA(x,y);
			if (op==1)
			{
     
				tot++;
				if (LCA==x)	{
     h[tot].LCA=0;h[tot].l=L[x];h[tot].r=L[y];h[tot].id=u;}
				else	{
     h[tot].LCA=LCA;h[tot].l=R[x];h[tot].r=L[y];h[tot].id=u;}
			}
			else	ans[u]=case2(x,y,LCA);
		}
		case1();
		///printf("%d\n",num1);
		for (int u=1;u<=m;u++) printf("%lld\n",ans[u]);
	}
	return 0;
}