图的遍历（深度、广度、最小生成树、最短路径）

 有向连通图如下所示

 

 

#include
#include
#include 
#include 
#include 
#include 
#include 
#define MAXV 7									//最大顶点个数
#define INF unsigned short(-1)					//定义 ∞ 
//∞ == INF(表示 两点不可直达)
//深度优先遍历：Depth First Search （DFS） 
//广度优先比例：Breadth First Search （BFS） 

typedef struct eNode {
	int adjVer;					//该边的邻接点编号 
	int weight;					//该边的的信息，如权值 
	struct eNode* nextEdge;		//指向下一条边的指针 
}EdgeNode; 						//别名，边结点的类型 

typedef struct vNode {
	EdgeNode* firstEdge;		//指向第一个边结点 (其实数组比较方便)
}VNode; 						//别名，邻接表的头结点类型 

typedef struct list
{
	int vertexCnt;				//顶点个数
	int edgeCnt;				//边数
	VNode adjList[MAXV];		//邻接表的头结点数组 
}ListGraph;						//别名，完整的图邻接表类型 

								// 每个顶点到最近其他顶点的数据
typedef struct closedge
{
	int adjVer;	// 最近邻接顶点
	int weight;	// 两顶点的权重
}Closedge;
Closedge PrimClosedge[MAXV] = { 0 };

// 边
typedef struct edge
{
	edge(int v1, int v2, int w) :ver1(v1), ver2(v2), weight(w) {}
	int ver1;	// 顶点1
	int ver2;	// 顶点2
	int weight;	// 两顶点的权重
}Edge;

struct EdgeSortFun
{
public:
	bool operator()(const Edge& a, const Edge& b)// 按权重升序
	{
		return a.weight < b.weight;
	}
};

// 最短路径:贝尔曼福特算法(Bellman_Ford算法)，Floyd算法的优化(因为只针对v0点，从二维降到一维)
// 作用：计算不含负圈图的最短路径 返回是否有圈
// v到各点的距离
bool ShortestPath_Bellman_Ford(int matrix[MAXV][MAXV], int v0 = 0,int val = 6)
{
	int D[MAXV] = { 0 };		// v0点到其余各点的距离
	int Path[MAXV] = { 0 };		// 前置点
	//初始化
	for (int i = 0; i < MAXV; i++)
	{
		D[i] = matrix[v0][i];
		if (D[i] && D[i] != INF)
			Path[i] = v0; // i为v的邻接点
		else 
			Path[i] = -1;
	}
	D[v0] = 0;

	//初始化结束，开始双重循环
	for (int k = 0; k < MAXV ; ++k)
	{
		for (int i = 0; i < MAXV; ++i) //i为源点
		{
			for (int j = 0; j < MAXV; j++) //j为终点
			{
				if (D[i] + matrix[i][j] < D[j])// v0到i + i到j < v0到j
				{
					D[j] = D[i] + matrix[i][j];// 更新距离
					Path[j] = i;	// 更新j前置
				}
			}
		}
	}
	//判断是否含有负圈
	bool flag = true;
	for (int j = 0; j < MAXV; j++) //j为源点
	{
		for (int k = 0; k < MAXV - 1; k++) //k为终点
		{
			if (D[k] > D[j] + matrix[j][k])
			{
				flag = false;
				break;
			}
		}
	}

	// 输出
	std::cout << v0 << "点到其他各点的最短路径:" << std::endl;
	for (int i = 0; i < MAXV; ++i)
	{
		if (i != v0)
		{
			std::cout << "--> 点" << i;
			if (D[i] != INF)
				std::cout << " 距离为: " << D[i] << std::endl;
			else
				std::cout << " 不可达" << std::endl;
		}
	}

	std::cout << "顶点" << v0 << " 到 " << val << "的路径为:" << std::endl;
	std::cout << val << "<-";;
	while (Path[val] != 0)
	{
		std::cout << Path[val] << "<-";
		val = Path[val];
	}
	std::cout << v0 << std::endl;
	return flag;
}

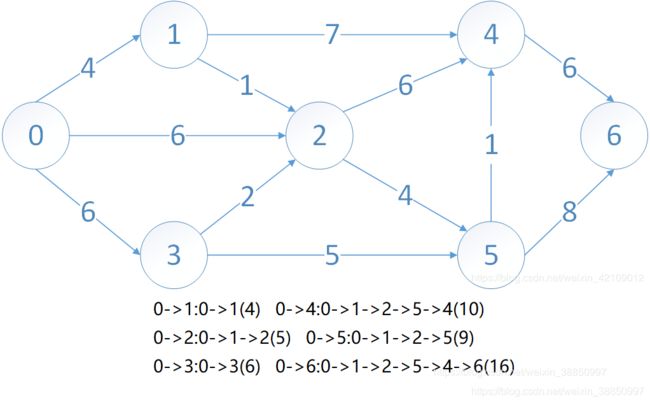
// 最短路径:迪杰斯特拉算法(Dijkstra算法)
// 计算v0点到其他点的最短距离
void ShortestPath_Dijkstra(int matrix[MAXV][MAXV], int v0 = 0, int val = 6)
{
	std::cout << v0 << "点到其他各点的最短路径:" << std::endl;

	bool S[MAXV] = { 0 };	// v0到vi点的最短路径是否已经被确定
	int D[MAXV] = { 0 };	// v0到vi点的最短路径，否则为INF
	int Path[MAXV] = { 0 };	// vo到vi的最短路径上vi的(当前)前驱节点,默认-1
	for (int i = 0; i < MAXV; ++i)
	{
		S[i] = false;
		D[i] = matrix[v0][i];
		if (D[i] && D[i] != INF)// i点是v0点的邻接点(v0为前驱顶点)
			Path[i] = v0;
		else
			Path[i] = -1;// 当前点 或是 非邻接点
	}
	// 当前点
	S[v0] = true;
	D[v0] = 0;
	Path[v0] = -1;

	// 循环，每次求得v0到某个顶点v的最短路径,将v加入到S
	for (int i = 1; i < MAXV; ++i)
	{
		int min = INF;
		int v = -1;	// 顶点v
					// 遍历D,找到没被确定的距离最短的那个点
		for (int j = 0; j < MAXV; ++j)
		{
			if (!S[j] && D[j] < min)// j该点没被确定 且 到该点的路径较短
			{
				v = j;				// 记录当前v0能到达距离最短的那个点v
				min = D[j];			// 记录当前v0能到达点的最小距离
			}
		}
		if (v != -1)
			S[v] = true;// 确定到v点为最短
		else
			continue;
		for (int j = 0; j < MAXV; ++j)
		{
			if (!S[j] && (D[v] + matrix[v][j] < D[j]))// 从剩余没被确定的点j中，比较 [v0到v的距离(已确定) + 点v到j的距离](该距离为增加中间新顶点后，v0到j的新可达路径v0->v->j的距离) 和 当前j到点v0的距离(原j到v0的最短库里)，选取较小的值
			{	// 如顶点0->1,0->2的原路径为0->1,0->2，最短分别为D[1]=4，D[2]=6，由于v(点1)被确定到S，得到新路径 v0->v(点1)->j(点2),最短为D[v] + matrix[v][j] = 5 < D[j] = 6;更新j(2)到原点的距离
				D[j] = D[v] + matrix[v][j];
				Path[j] = v;	// v中间节点为新的前置节点
			}
		}
	}

	// 输出
	for (int i = 0; i < MAXV; ++i)
	{
		if (i != v0)
		{
			std::cout << "--> 点" << i;
			if (D[i] != INF)
				std::cout << " 距离为: " << D[i] << std::endl;
			else
				std::cout << " 不可达" << std::endl;
		}
	}
	std::cout << "顶点" << v0 << " 到 " << val << "的路径为:" << std::endl;
	std::cout << val << "<-";;
	while (Path[val] != 0)
	{
		std::cout << Path[val] << "<-";
		val = Path[val];
	}
	std::cout << v0 << std::endl;
}

// 最短路径:弗洛伊德算法(Floyd算法)
// 输出v0点到其他点的最短距离
void ShortestPath_Floyd(int matrix[MAXV][MAXV], int v0 = 0, int val = 6)
{
	int D[MAXV][MAXV] = { 0 };		// D[i][j],记录两顶点i，j的最短距离
	int Path[MAXV][MAXV] = { 0 };	// Path[i][j],记录顶点i到j路径上,j当前的前置顶点

	for (int i = 0; i < MAXV; ++i)
	{
		for (int j = 0;j < MAXV; ++j)
		{
			D[i][j] = matrix[i][j];// 初始化顶点i到到j的当前最短距离
			// 初始化每个顶点到其他顶点的前置顶点
			if (D[i][j] && D[i][j] != INF)	// 邻接点
				Path[i][j] = i;
			else
				Path[i][j] = -1;
		}
	}

	for (int k = 0; k < MAXV; ++k)			// 假设从i到j要经过k
	{
		for (int i = 0; i < MAXV; ++i)
		{
			for (int j = 0; j < MAXV; ++j)
			{
				if (D[i][k] + D[k][j] < D[i][j])
				{
					D[i][j] = D[i][k] + D[k][j];
					Path[i][j] = Path[k][j];		// 更改j的前驱为k
				}
			}
		}
	}

	// 输出
	std::cout << v0 << "点到其他各点的最短路径:" << std::endl;
	for (int i = 0; i < MAXV; ++i)
	{
			if (i != v0)
			{
				std::cout << "--> 点" << i;
				if (D[v0][i] != INF)
					std::cout << " 距离为: " << D[v0][i] << std::endl;
				else
					std::cout << " 不可达" << std::endl;
			}
	}

	std::cout << "顶点" << v0 << " 到 " << val << "的路径为:" << std::endl;
	std::cout << val << "<-";;
	while (Path[v0][val] != 0)
	{
		std::cout << Path[v0][val] << "<-";
		val = Path[v0][val];
	}
	std::cout << v0 << std::endl;
}

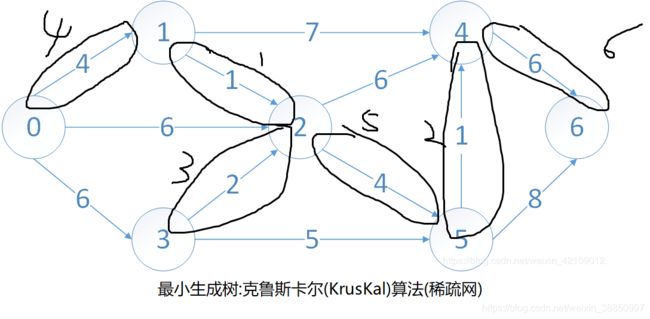
// 最小生成树：克鲁斯卡尔算法(kruskal算法)
void MiniSpanTree_Kruskal(int matrix[MAXV][MAXV])
{
	int vexset[MAXV] = { 0 };// 联通分量
	for (int i = 0; i < MAXV; ++i)
	{
		vexset[i] = i;// 初始化每个点为联通分量
	}
	std::deque edge;
	for (int i = 0; i < MAXV; ++i)
	{
		for (int j = 0; j < MAXV; ++j)
		{
			if (matrix[i][j] && matrix[i][j] != INF)
			{
				Edge e(i, j, matrix[i][j]);
				edge.push_back(e);
			}
		}
	}
	std::sort(edge.begin(), edge.end(), EdgeSortFun());

	for (int i = 0; i < MAXV && !edge.empty(); )
	{
		// 当前最小变得两个顶点
		int v1 = edge.front().ver1;
		int v2 = edge.front().ver2;
		// 两个点的所在联通分量
		int vs1 = vexset[v1];
		int vs2 = vexset[v2];
		if (vs1 != vs2)// 若相同则出现环
		{
			std::cout << "边:顶点" << v1 << "--" << v2 << std::endl;
			for (int j = 0; j < MAXV; ++j)// 用for循环是因为，你不知道vs1和vs2下，联通分量中的顶点数是1：n还是n：1，如果能立马判断出vs1下的是1的话，只需要vexset[v1] = vs2即可
			{
				if (vexset[j] == vs2) vexset[j] = vs1;// 都改成同一个联通分量，所以if (vexset[j] == vs1) vexset[j] = vs2;也行
			}
			++i;
		}
		edge.pop_front();
	}

	int c = 0;
}

int Min(Closedge PrimClosedge[MAXV])
{
	int min = INF;
	int idx = -1;
	for (int i = 0; i < MAXV; ++i)
	{
		if (PrimClosedge[i].weight > 0 && PrimClosedge[i].weight < min)
		{
			min = PrimClosedge[i].weight;
			idx = i;
		}
	}
	return idx;
}
// U表示已经有选定最小边的顶点(起始为rootVer),V表示所有顶点
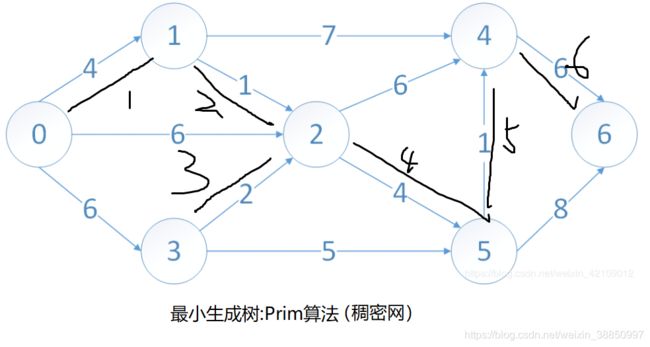
// 最小生成树：普拉姆(prim算法)，根据邻接矩阵表示
void MiniSpanTree_Prim(int matrix[MAXV][MAXV], int rootVer = 0)
{
	// 根节点(U={rootVer(0)}) 到 其他节点的最小距离
	for (int i = 0; i < MAXV; ++i)
	{
		if (i != rootVer)// 其他节点
		{
			PrimClosedge[i].adjVer = rootVer;
			PrimClosedge[i].weight = matrix[rootVer][i];
		}
	}

	for (int i = 1; i < MAXV; ++i)
	{
		int minVerIdx = Min(PrimClosedge);		// 当前最小边的那个顶点

		if (minVerIdx == -1) break;// 非连通图出错

		int u = PrimClosedge[minVerIdx].adjVer;	// 该边的一个顶点		u 属于U
		int v = minVerIdx;						// 该边的另一个顶点		v 属于V-U
		std::cout << "边:顶点" << u << "--" << v << std::endl;
		PrimClosedge[minVerIdx].weight = 0;		// 顶点并入U，(即v到u顶点的边不用在计算了)
												// U += {minVerIdx}
												// 比较其u,v到 他节点j的权重，若uj > vj；则修改j目前的最近邻接顶点为v
		for (int j = 0; j < MAXV; ++j)
		{
			if (matrix[minVerIdx][j] < PrimClosedge[j].weight)// 比较 当前最小边的顶点v和u 分别 到  其他顶点 的权重 
			{
				// 如在确定0(u)--1(v)边后，matrix[1][2] = 1(1到2的权重) < PrimClosedge[2].weight = 6(0到2的权重)
				// 得到PrimClosedge[2].adjVer = 1;即U{0,1}中的1 到 2 最近
				PrimClosedge[j].adjVer = minVerIdx;
				PrimClosedge[j].weight = matrix[minVerIdx][j];
			}
		}
	}
	return;
}


//创建图的邻接表 
void CreateAdjListGraph(ListGraph* &LG, int matrix[MAXV][MAXV], int vertexCnt, int edgeCnt)
{
	int i, j;
	EdgeNode* p;
	LG = (ListGraph*)malloc(sizeof(ListGraph));
	for (i = 0; i < vertexCnt; i++)
	{
		LG->adjList[i].firstEdge = NULL;		//给邻接表中所有头结点指针域置初值 
	}
	for (i = 0; i < vertexCnt; i++) 			//检查邻接矩阵中的每个顶点元素 
	{
		for (j = vertexCnt - 1; j >= 0; j--)	// 该顶点到其余点的数据
		{
			//if (matrix[i][j] != 0) 								//存在一条边 
			{
				p = (EdgeNode*)malloc(sizeof(EdgeNode));		//申请一个结点内存
				p->adjVer = j;									//存放邻接点 
				p->weight = matrix[i][j];						//存放权值
				p->nextEdge = NULL;

				p->nextEdge = LG->adjList[i].firstEdge;			//头插法 
				LG->adjList[i].firstEdge = p;
			}
		}
	}
	LG->vertexCnt = vertexCnt;
	LG->edgeCnt = edgeCnt;
}

//输出邻接表 
void DisplayAdjList(ListGraph* LG)
{
	int i;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++)
	{
		p = LG->adjList[i].firstEdge;
		printf("%d:", i);
		while (p != NULL)
		{
			if (p->weight != INF) // 输出当前等点能直达的邻接顶点信息
			{
				printf("%2d[%d]->", p->adjVer, p->weight);
			}
			p = p->nextEdge;
		}
		printf(" NULL\n");
	}
}

//深度优先遍历
bool visitedDFS[MAXV] = { 0 };									//全局数组，记录当前顶点是否已经遍历
void DFS(ListGraph* LG, int matrix[MAXV][MAXV], int v)
{
	/*
	// 通过邻接表遍历
	EdgeNode* p;
	visitedDFS[v] = true;										//记录已访问
	std::cout << v << " ";										//输出顶点编号
	p = LG->adjList[v].firstEdge;								//p 指向顶点 v 的第一个邻接点
	while (p)
	{
		if (!visitedDFS[p->adjVer] && p->weight != INF) 		//如果下一个邻接节点 p->adjVer 没被访问，递归访问它
		{
			DFS(LG, p->adjVer);
		}
		p = p->nextEdge;										//p 指向顶点 v 的下一个邻接点
	}
	*/

	// 通过邻接矩阵遍历
	std::cout << v << " ";
	visitedDFS[v] = true;
	for (int i = 0; i < MAXV; ++i)
	{
		if (matrix[v][i] && matrix[v][i] != INF && !visitedDFS[i])
		{
			DFS(LG, matrix, i);
		}
	}
}

void DFS1(ListGraph* LG, int matrix[MAXV][MAXV])
{
	memset(visitedDFS, 0, sizeof(visitedDFS));
	for (int i = 0; i < LG->vertexCnt; ++i)
	{
		if (!visitedDFS[i])
			DFS(LG, matrix, i);
	}
}

bool visitedBFS[MAXV] = { 0 };
//广度优先遍历
void BFS(ListGraph* LG, int matrix[MAXV][MAXV], int v)
{
	/*通过邻接表遍历*/
	/*
	std::deque d;
	visitedBFS[v] = true;
	d.push_back(LG->adjList[v].firstEdge);
	std::cout << v << " ";
	while (!d.empty())
	{
		EdgeNode* p = LG->adjList[d.front()->adjVer].firstEdge;		// 下一个访问的邻接节点的头结点 
		d.pop_front();
		while (p)
		{
			if (!visitedBFS[p->adjVer] && p->weight != INF) // 未访问过
			{
				std::cout << p->adjVer << " ";
				d.push_back(p);	// 未访问过的邻接节点的头结点 
				visitedBFS[p->adjVer] = true;
			}
			p = p->nextEdge;
		}
	}
	*/

	
	// 通过邻接矩阵遍历
	std::deque d;
	d.push_back(v);
	visitedBFS[v] = true;
	while (!d.empty())
	{
		int front = d.front();
		for (int i = 0; i < MAXV; ++i)
		{
			if (matrix[front][i] && matrix[front][i] != INF && !visitedBFS[i])
			{
				visitedBFS[i] = true;
				d.push_back(i);
			}
		}
		std::cout << front << " ";
		d.pop_front();
	}
}
void BFS1(ListGraph* LG, int matrix[MAXV][MAXV])
{
	memset(visitedBFS, 0, sizeof(visitedBFS));
	for (int i = 0; i < LG->vertexCnt; ++i)
	{
		if (!visitedBFS[i])
			BFS(LG, matrix, i);
	}
}

int main()
{
	ListGraph* LG = nullptr;
	// 对应的邻接矩阵
	int matrix[MAXV][MAXV] =
	{
		 (有向非连通图，顶点6独立)
		//{ 0,   4,   6,   6, INF, INF, INF },
		//{ INF,   0,   1, INF,   7, INF, INF },
		//{ INF, INF,   0, INF,   6,   4, INF },
		//{ INF, INF,   2,   0, INF,   5, INF },
		//{ INF, INF, INF, INF,   0, INF,  INF },
		//{ INF, INF, INF, INF,   1,   0,  INF },
		//{ INF, INF, INF, INF, INF, INF,   0 }
		// 有向连通图
		{ 0,   4,   6,   6, INF, INF, INF },
		{ INF,   0,   1, INF,   7, INF, INF },
		{ INF, INF,   0, INF,   6,   4, INF },
		{ INF, INF,   2,   0, INF,   5, INF },
		{ INF, INF, INF, INF,   0, INF,   6 },
		{ INF, INF, INF, INF,   1,   0,   8 },
		{ INF, INF, INF, INF, INF, INF,   0 }

		 无向连通图
		//{   0,   4,   6,   6, INF, INF, INF },
		//{   4,   0,   1, INF,   7, INF, INF },
		//{   6,   1,   0,   2,   6,   4, INF },
		//{   6, INF,   2,   0, INF,   5, INF },
		//{ INF,   7,   6, INF,   0,   1,   6 },
		//{ INF, INF,   4,   5,   1,   0,   8 },
		//{ INF, INF, INF, INF,   6,   8,   0 }
	};

	int edgeCnt = 12;// 两个点之间连线,即边Edge的数量，通过遍历上述数组，统计非0和INF数量即可
	CreateAdjListGraph(LG, matrix, MAXV, edgeCnt);

	std::cout << "邻接表为：" << std::endl;
	DisplayAdjList(LG);
	std::cout << std::endl;

	std::cout << "深度优先遍历为(仅适用于非连通图)：" << std::endl;
	DFS(LG, matrix, 0);		// 0 1 2 4 6 5 3
	std::cout << std::endl;
	std::cout << "深度优先遍历为(也使用非连通图)：" << std::endl;
	DFS1(LG, matrix);
	std::cout << std::endl;


	std::cout << "广度优先遍历为(仅适用于非连通图)：" << std::endl;
	BFS(LG, matrix, 0);		// 0 1 2 3 4 5 6
	std::cout << std::endl;
	std::cout << "广度优先遍历为(也使用非连通图)：" << std::endl;
	BFS1(LG, matrix);
	std::cout << std::endl;

	std::cout << "Prim算法:最小生成树的各边:" << std::endl;
	MiniSpanTree_Prim(matrix, 0);

	std::cout << "Kruskal算法:最小生成树的各边:" << std::endl;
	MiniSpanTree_Kruskal(matrix);

	std::cout << "Dijkstra算法:最短路径:" << std::endl;
	ShortestPath_Dijkstra(matrix, 0);

	std::cout << "Floyd算法:最短路径:" << std::endl;
	ShortestPath_Floyd(matrix, 0);

	std::cout << "Bellman_Ford算法:最短路径:" << std::endl;
	ShortestPath_Bellman_Ford(matrix, 0);
	return 0;
}