由浅至深->C语言中位运算的相关问题

引言： 位(bit)这个概念在计算机基础or数字电路中可多次寻得其身影，且对于嵌入式开发人员而言也是一份极其重要的知识。理论上可以通过位运算来完成所有的运算和操作，但现在的计算机编程语言大多都不涉及这么细节和底层的操作，因而C语言才成为嵌入式开发的优选。不过对于多数读者而言，或许不会从事嵌入式开发的相关工作，但若习得一些位操作的知识，必然可以有效地提高所编写程序的运行效率。

文章向导
按位与(或)运算符的使用
按位异或运算符的使用
移位运算符的使用

一、按位与(或)运算符的使用

1.基础用法
　　按位与运算通常用来对某些位清零或保留某些位，而这种用法也被称之为“掩码”，下面以一个字节的数据来举例说明。

char test = 0x96; //10010110
char mask = 0x03; //00000011
test &= mask; //00000010  
test |= mask; //10010111  设置位
test &= ~mask; //10010100 清零位

       上述程序片段仅是为了说明问题，其中test与mask的值在多次运算中均是使用最初的设定值(实际程序肯定不是如此)。在按位与运算中，不透明的0掩盖了test中相应的位，透明的1则保留了test中相应的位；在按位或运算中，透明的1打开了test中相应的位，不透明的0则对test无影响；在最后所谓的“清零位”操作中，mask中为1的位取反后则清零了test中相应的位，而为0的位取反后则对test中相应的位无影响。

2.实用技巧
       先引入一个问题“如何统计出变量a表示为二进制时，其中1或0的个数”？显然，涉及到单个位上的数据问题时，用位运算操作的方式来解决会比较高效和便捷。
       下面先给出具体可用的示例程序，接着再剖析其原理(为不致于使读者理解起来过于复杂，故仅贴出main.c的代码, 其余文件中的代码仅给出截图，感兴趣的读者自行阅读)：

#include "binbit.h"

int fun1(int a, char* str){
       //统计a的二进制中1的数目
	
	int count = 0; 
	
	while(a!=0x00){
     
		itobs(a, str);   //整数a转换为二进制字符串 
		printf("第%d次: ", count);
		show_bstr(str);  //打印每次运算后的二进制字符串 
		putchar('\n');
		a = a & (a-1); //相当于每次消灭一个1 
		count++;
	}
	
return count;
}

int fun2(int a, char* str){
       //统计a的二进制中0的数目
	
	int count = 0; 
	
	while(a!=0xFF){
     
		itobs(a, str);   //整数a转换为二进制字符串 
		printf("第%d次: ", count);
		show_bstr(str);  //打印每次运算后的二进制字符串 
		putchar('\n');
		a = a | (a+1); //相当于每次消灭一个0
		count++;
	}
	
return count;
}

int main(void){
     
	
	char bin_str[SIZE + 1]; //+1: 末尾结束字符 
	
	printf("(1): %d\n", fun1(0xFF, bin_str)); //统计1的个数 
	printf("(0): %d\n", fun2(0x00, bin_str)); //统计0的个数
	
	return 0;
}

其他代码：


运行结果：

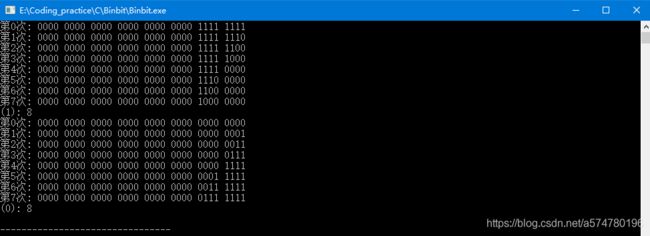
       显然，此时问题的关键全都集中于如何正确理解a = a & (a-1); a = a | (a+1) 这两条语句各自的含义。
(1) a = a & (a-1), 为方便说明问题不妨设a=0x03 //00000011
       由二进制的减法运算规则可知：若a最低位为1，则执行a-1时则消掉了最低位（最右边）的1；若a最低位为0, 则执行a-1时会向前借位从而又消掉一个1。
       从而可知，a=0x03执行两次a-1后则用掉了a中所有的1。
(2) a = a | (a+1)，同理不妨设a=0x00 //00000000
       此时，读者应该可以自行分析出：根据二进制的加法运算规则，每执行一次a+1则会引入一个1。

二、按位异或运算符的使用

       设有两个变量a和b, 若从微观层面(单个bit)来观察，按位异或运算规则可简单概况为“相异为1, 相同为0”；若从宏观的变量角度来观察，则可导出下列运算规则：
a ⊕ a = 0         a ⊕ b = b ⊕ a
a ⊕ b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c
d = a ⊕ b ⊕ c        =>        a = d ⊕ b ⊕ c =a ⊕ (b ⊕ c ⊕ b ⊕ c) ，
a ⊕ b ⊕ a = b
       上述运算规则乍一看似乎没什么太大用处，但这份运算规则中其实暗含着交换两个变量值的高效方法。关于这一点的体悟，笔者想通过一个实际的例子来向大家说明。

#include

#define SWAP1(a,b)\
{                 \
	int t = a;    \
	a = b;        \
	b = t;        \
} 

#define SWAP2(a,b)\
{                 \
	a = a + b;    \
	b = a - b;    \
	a = a - b;    \
} 

#define SWAP3(a,b)\
{                 \
	a = a ^ b;    \
	b = a ^ b;    \
	a = a ^ b;    \
} 

int main(void){
     
	
	int a = 3, b= 4;
	
	printf("a = %d, b = %d\n", a, b); // 3 4
	
	SWAP3(a,b);
	
	printf("a = %d, b = %d\n", a, b); //4 3
	
	return 0;
}

       该程序中出现了三种交换变量的方法，其中SWAP1应该是大多数读者都熟悉的操作，而SWAP2与SWAP3或许则鲜为人知。论效率和实现来看，SWAP3效率最高。同时，SWAP2在多数情况下虽然也能完成变量值交换的任务，但实际隐藏着一个尴尬的bug(即当a,b数值较大时, 其部分和a+b则会发生溢出，从而使得之后的交换不能正确进行)。

三、移位运算符的使用

1.基本规则

• 左移(如a<
• 右移(如a>>x)：将运算数a的二进制位右移x个单位，其中高位补符号位，低位丢弃；
• 注1：左操作数a必须为整数类型，即若a为char和short类型将被隐式转换为int后进行移位操作；
• 注2：按照标准C规范，右操作数x的范围必须为[0,31]，若x为负数，其移位结果则有编译器厂商自行定义。
  了解移位运算符的基本规则后，不妨通过一个实际例子来加以体悟(下例中用到了前面例子中所编写的函数体)

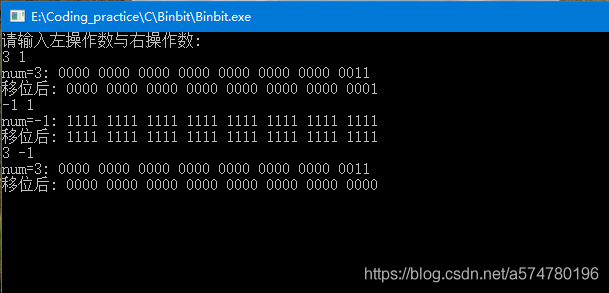
int main(void){
     
	
	char bin_str[SIZE + 1]; //+1: 末尾结束字符 
	int num, shift;
	
	puts("请输入左操作数与右操作数: ");
	while(scanf("%d %d", &num, &shift) == 2){
     
		printf("num=%d: ", num);
		itobs(num, bin_str); 
		show_bstr(bin_str);  
		putchar('\n');
		printf("移位后: ");
		itobs(num>>shift, bin_str); 
		show_bstr(bin_str);  
		putchar('\n');
	}	
	return 0;
}

运行结果：

2. 实用技巧
       刚才的例子只是为了说明移位运算符的基本规则，实际编程工作中倒并无太大用处。在文章的首部，我们提到了“理论上可通过位运算完成所有的运算和操作”，那么移位运算符的妙用则在于可快速进行2的n次幂的运算，以及提取较大单元中的单个字节的数值or组合多个字节单元的数值为一个整体。
       下面通过例子来具体说明提取以及组合字节数值这点。

int main(void){
     
	
	#define BYTE_MASK 0xFF

	char bin_str[SIZE + 1]; //+1: 末尾结束字符 
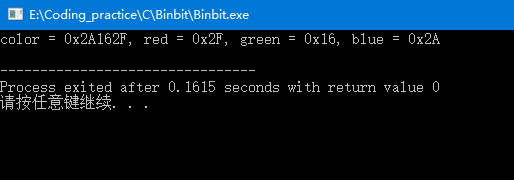
	unsigned long color = 0x002a162f;
	unsigned char blue, green, red;
	
	red = color & BYTE_MASK;  //提取红色分量
	green = (color>>8) &  BYTE_MASK;  //提取绿色分量
	blue = (color>>16) &  BYTE_MASK;  //提取蓝色分量
	
	printf("color = 0x%X, red = 0x%X, green = 0x%X, blue = 0x%X\n", color, red, green, blue);
		
	return 0;
}

运行结果：

参阅资料

1. 狄泰软件学院-C进阶剖析教程
2. C primer plus 第6版
3. 高质量嵌入式Linux C
4. 算法精解-C语言描述