算法修行第一弹：一切从观察开始——趣题探索

文章向导

算法与观察的关系

小试牛刀1：n人排队报数(约瑟夫环问题雏形)

小试牛刀2：n盏灯(百盏灯问题)

一、算法与观察的关系

     ~~~~          ~~~    当谈及算法的面貌时，人们首先联想到的会是诸如数据结构书本中所提到的抽象定义，又或是繁杂庸长的数学公式。虽然也知道算法的重要性，但畏惧心理在与算法的初次见面时则已布满全身。
　　笔者曾在数据结构的书中寻得算法的定义——即解决特定问题求解步骤的描述，在计算机中则表示为特定的指令序列(输入->输出，这样的过程)。随着学习的深入与积累的感悟，这种抽象的定义也被我抛在一旁，说白了算法就是解决特定问题的方法而已，只不过存在多种可选择的方法，它们之间也存在着一定的优劣对比。
　　那么想要设计或者使用算法，无疑都是从最初的观察开始入手。当你对目前所面对的问题有了较为充分的观察和认识后，就可以开始尝试所设想的方法或手段（不管是自创还是占在巨人的肩膀上）。本文也正是从这样的角度进行切入，从生活中一些实际的例子出发，体悟观察的必要性。

二、小试牛刀１：ｎ人排队报数问题

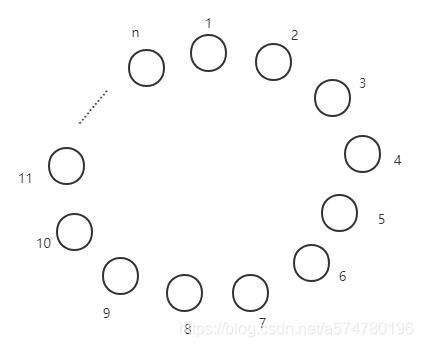
　　这个问题大致说的是：n个人围城一圈，按照1~n顺序进行编号，并从第一个人开始反复报数(从1报到k)，凡是报到k的人就立即退出圈子而剩下的人继续报数。最后整个圈子中只会剩下一个人，求最后剩下的那个人是原来的几号？

【分析】问题乍一看起来貌似还有些复杂，或许会存在以下几点疑问：

1) 若通过编程(C/C++)来解决，对n个人进行顺序编号可以使用数组来记录，但如何处理某个人是否在场或是出局呢？

2) 如何模拟反复报数，并剔除圈子中特定出局的人？

3) 当有人出局后圈子也会发生变化，那么对应的数组队伍需要进行调整吗？若调整是否会影响编号的获取？
　　
　　为了解决初次面对时所产生的疑问，还需要对问题进行进一步的观察与分析。首先不妨在纸上画一份数组，同时为了方便分析，下图中以k=3来进行说明。

　　既然是顺序编号，那么不妨舍弃数组下标为0的元素，剩余的元素则用于一一对应圈子中的n个人。同时也可以用数组的内容来记录参与者是否在场或是出局。报数前，将整个数组的值设定为1代表圈子中的人最初都在场。
　　
　　按照指定的规则进行报数，不断的剔除特定的参与者，此时数组队伍的状态如下图所示：

　　即报数为3的人，我们将其数组元素值设定为0代表其出局，而剩下元素值为1的则继续进行报数游戏，直到最后只剩一人为止。
　　这样分析下可发现，由于数组的顺序存储结构特性，我们不必在有人出局后对数组队伍进行调整，虽然在实际生活中进行游戏时会有圈子上的调整，但在用计算机处理时则不必考虑这个问题。因为这样并不会对编号的获取造成影响，相反若调整了数组队伍，则无疑复杂了问题的求解。
　　
　　问题分析到这儿，差不多也可进行实际的编码工作。但问题(2)我们依然没有完全解决，即如何让计算机知道指定的报数情况从而剔除特定的参与者。此时则得细致观察数组队伍的特点，从中发掘可利用的条件。
　　细致观察后可发现，当指定报数参数k=3时，若累计数组元素的值为3时刚好就对应着要剔除的人，这样反复累计数组元素值不就相当于模拟了报数，从而解决问题。

【求解】下面通过实际编码来解决问题，以C++为例。

#include

using namespcae std;

int main()
{
	int n, k, stu_num;
	int sum = 0, stu[100]={0};
	
	cout<<"请输入参与者数量和报数参数\n";
	cin>>stu_num>>k; //输入参与者数量和报数参数
	n = stu_num; //控制for循环
	
	/*(准备报数) -> 注意不要使用memset*/
	for (int i=1; i<=n; i++){  //此时都在场，全置为1
		stu[i] = 1;
	}
	
	/*(开始报数)*/
	if (k==1){
		printf("留下的那位参与者的编号为: %d\n", n);  //此时最后一位编号的人留下
		for(int i=1; i<=n-1; i++){  //其他人都出局
			stu[i] = 0;
		}
		
	}else{
		while (stu_num > 1){  //退出条件为最后只剩一位人
		
			/*利用for循环模拟n人报数*/
			for (int i=1; i<=n; i++){
				sum += stu[i];
				if (sum == k){    //sum累加和为k, 代表报数到k
					stu[i] = 0;  //该参与者出局
					sum = 0;    //重新从1开始报数
					stu_num--;
					if (stu_num == 1){  //k等1时有的情况,因为要求最后剩1人
						break;
					}
				}
			}
		}
		/*游戏结束,谁在场上?*/
		for (int i=1; i<=n; i++){
			if (stu[i]){  	//1在场, 0出局
				printf("留下的那位参与者的编号为: %d\n", i);
			}
		}
	}
		
return 0;
}

     ~~~~          ~~~    以上已经给出了该问题的具体实现，读者可结合题目描述细细品味分析。其中，给出的C++代码也有值得强调的两处地方：

• 准备报数阶段：此时应将stu[]数组置为1，但文中用的for循环来达成这一目的。或许有些读者觉得用memset函数不就简单搞定了么？但实际上memset若对int型数组进行初始化，其值只能设定为0和-1，具体原因读者可查阅相关资料，了解其使用方法和注意事项。
• 开始报数阶段：应对报数参数k的取值情况进行讨论，剥离k=1时这种特殊情况，若不进行剥离统一按照while(stu_num>1)里的方法进行处理，则最终圈子中将一人不剩。

三、小试牛刀2：n盏灯问题

     ~~~~          ~~~    接下来这个问题描述的是，有按1~n顺序编号的n盏灯，同时有k个人会对这n盏灯分别进行不同的操作：第1个人会把所有灯都打开；第2个人将按下所有编号为2的倍数的开关(这些灯将被关闭)；第3个人按下所有编号为3的倍数的开关(其中关掉的灯将被打开,打开的灯将被关掉)，依次类推。
　　最后问还有哪些灯是打开的？ 其中，参数关系限制为(k<=n<=1000)。

【分析】

• 由于最开始所有灯都是关着的，故只有经过奇数次改变开关状态的灯是亮着的。故此时应着手分析灯编号与人编号的数字关系。
• 根据题意进一步分析可知，一个数字有多少个因数就要开关多少次，故最后亮着的灯为：灯编号有奇数个不同的因数。
• 一个数的因数按出现的奇偶个数划分有如下两种情况：
  ①因数有单个出现的，如36的因数对：(1,36)、(2,18)、(3,12)、(4,9)、(6)
  ②因数是成对出现的，如8的因数对：(1,8)、(2,4)

     ~~~~          ~~~    如上分析可知1~n中只有平方数才会出现奇数个整型因数，若目前有100盏灯，则很快能推断出最后编号为1,4,9,16,25,36,49,64,84,100这些灯是亮着的。
　　但若想通过编程的方式求解此问题，同样可创建一个数组用来记录n盏灯，其值为1代表On，为0代表Off。
　　但此时有k个人，他们各自所对应的操作则会改变此数组的内容。那么，不妨画出一份表格：行(横排)编号描述k个人，列(竖排)编号描述n盏灯，表格具体情况如下：

　　图中为了方便说明问题，ｎ取值为10，k取值为4。画出了表格进一步观察该如何表达出灯编号与人编号之间的倍数关系，从而对应不同的操作。
　　首先设人编号为i，灯编号为j，因两者是因数关系，故可以使用j%i==0这种方式来表达。代入表格验证，也发现是初步符合问题描述的。不仅可以表示第1个人将所有灯都打开，其余人也能对应上各自倍数的编号的灯。

【求解】下面给出了一份参考代码，较为简练。

#include

using namespace std;

int main()
{
	int n, k;
	int a[100] = {0};
	
	cout<<"请分别输入灯的数量和人的数量\n";
	cin>>n>>k;
	
	//1表示开灯，0表示关灯, 
	for(int i=1; i<=k; i++){
		for(int j=1; j<=n; j++){
			if(j%i==0){
				a[j] = !a[j];
			}
		}
	}
	
	for(int j=1; j<=n; j++){
		if(a[j]){
			printf("%d ", j);
		}
	}

return 0;
}

参阅资料

<图解算法.俞征武>