机器学习算法之bagging与随机森林算法
前言:在集成学习算法中,我们讲到了集成学习主要有两个流派,一个是boosting流派,它的特点是各个弱学习器之间有依赖关系。另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合。本文就对集成学习中Bagging与随机森林算法做一个总结。
随机森林是集成学习中可以和梯度提升树GBDT分庭抗礼的算法,尤其是它可以很方便的并行训练,在如今大数据大样本的的时代很有诱惑力。
1、bagging的原理
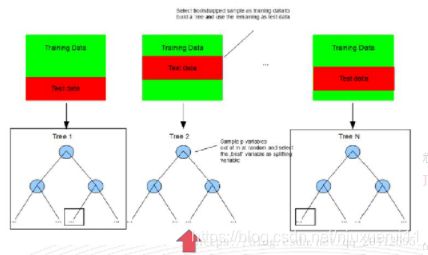
Bagging:基于数据随机重抽样的分类器构建方法。从训练集从进行子抽样组成每个基模型所需要的子训练集,对所有基模型预测的结果进行综合产生最终的预测结果。
**随机采样(bootsrap)**就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。对于我们的Bagging算法,一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同,但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样,,则由于随机性,T个采样集各不相同。
注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样,而Bagging的子采样是放回采样。
2、随机森林算法
RFR算法是由Leo Breiman和Adele Cutler[1]于2001年共同提出的一种基于决策树的集成学习算法。RFR算法是机器学习算法中精确度较高的算法,能克服单个预测或分类模型的缺点,被广泛应用于经济、医学、生物等领域。
2.1基本原理
理解了bagging算法,随机森林(Random Forest,以下简称RF)就好理解了。它是Bagging算法的进化版,也就是说,它的思想仍然是bagging,但是进行了独有的改进。
RF引入了bagging和随机子空间的思想。随机森林是一个用算法构建的没有剪枝的分类决策树的集合,森林的输出釆用简单多数投票法,或者是单棵树输出结果的简单平均得到。
具体的训练过程如下:
步骤1 利用bagging思想,随机产生样本子集。
步骤2 利用随机子空间思想,随机抽取f个特征,进行节点分裂,构建单棵回归决策子树。
步骤3 重复步骤1、步骤2,构建T棵回归决策子树,每棵树自由生长,不进行剪枝,形成森林。
步骤4 T棵决策子树的预测值取平均,作为最终结果
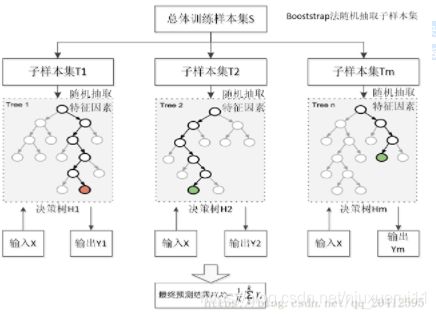
随机:数据采样随机,特征选择随机
森林:很多个决策树并行放在一起(决策树的详细讲解)
首先,RF使用了CART决策树作为弱学习器,这让我们想到了梯度提升树GBDT。第二,在使用决策树的基础上,RF对决策树的建立做了改进,对于普通的决策树,我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分,但是RF通过随机选择节点上的一部分样本特征,这个数字小于n,假设为n_{sub},然后在这些随机选择的n_{sub}个样本特征中,选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。
如果n_{sub}=n,则此时RF的CART决策树和普通的CART决策树没有区别。n_{sub}越小,则模型越健壮,当然此时对于训练集的拟合程度会变差。也就是说n_{sub}越小,模型的方差会减小,但是偏差会增大。在实际案例中,一般会通过交叉验证调参获取一个合适的n_{sub}的值。
除了上面两点,RF和普通的bagging算法没有什么不同, 下面简单总结下RF的算法。
2.2、随机森林的加深理解
1)对随机森林采样的理解
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是\small \frac{1}{m}。不被采集到的概率为\small 1-\frac{1}{m}。如果m次采样都没有被采集中的概率是\small (1-\frac{1}{m})^{m}。当\small m\rightarrow \infty时,\small (1-\frac{1}{m})^{m}=\frac{1}{e}\approx 0.368。也就是说,在bagging的每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集中。
对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(out of bag, 简称oob)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
袋外错误率(oob error,out-of-bag error):
3、随机森林算法参数
class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0, warm_start=False, class_weight=None)
对集成算法而言,有集成模型的框架参数,也有基模型的框架参数,我们要分清其中的意义。
首先我们关注于RF的Bagging框架的参数
1、n_estimators: 也就是弱学习器的最大迭代次数,或者说最大的弱学习器的个数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,计算量会太大,并且n_estimators到一定的数量后,再增大n_estimators获得的模型提升会很小,所以一般选择一个适中的数值。默认是100。
2、oob_score :即是否采用袋外样本来评估模型的好坏。默认是False。推荐设置为True,因为袋外分数反应了一个模型拟合后的泛化能力。
3、criterion: 即CART树做划分时对特征的评价标准。分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini,另一个可选择的标准是信息增益。回归RF对应的CART回归树默认是均方差mse,另一个可以选择的标准是绝对值差mae。一般来说选择默认的标准就已经很好的。
RF的决策树参数
决策树的框架参数这里就不做阐述。决策树的讲解部分有讲。
4、随机森林算法小结
最后也提一下,随机森林有很多的变种,感兴趣的可以自己研究。
优点:
1、预测效果比较好
2、训练可以高度并行化,对于大数据时代的大样本训练速度有优势。
3、能处理高维特征,不需要提前做特征过滤
4、不容易过拟合
5、模型训练速度快(相比Boosting),容易做并行化处理
6、能对特征的重要性排序
缺点:
1、对少量数据集和低维数据集的分类不一定可以得到很好的效果
2、执行速度虽然比Boosting等快,但还是比单个的决策树慢很多