数据结构入门系列——树和二叉树(2)
深入递归
设计一个递归算法求一个整数数组中所有元素之和。
设f(i)为整数数组a中a[0]~a[i-1]这i个元素之和,这是原问题。
小问题为f(i-1),它为a[0]~a[i-2]这i-1个元素之和。
假设f(i-1)已求出,显然有f(i)=f(i-1)+a[i-1],另外,f[1]=a[0]。对应的递归模型如下:
f ( 1 ) = a [ 0 ] f ( i ) = f ( i − 1 ) + a [ i − 1 ] f(1)=a[0] \quad f(i)=f(i-1)+a[i-1] f(1)=a[0]f(i)=f(i−1)+a[i−1]
int fun(int a[], int i)
{
if (i == 1) return a[0];
else return (fun(a, i - 1) + a[i - 1]);
}
二叉树存储结构
完全二叉树或满二叉树采用顺序存储结构比较合适,既能够最大可能地节省存储空间,又可以利用数组元素的下标确定结点在二叉树中的位置以及结点之间的关系。
若需要增加很多结点补做满二叉树,则用链式结构比较合适。
顺序存储
用一维数组按从上到下、从左到右的顺序存储树中所有结点值,通过数组元素的下标关系反映完全二叉树或满二叉树中结点之间的逻辑关系。
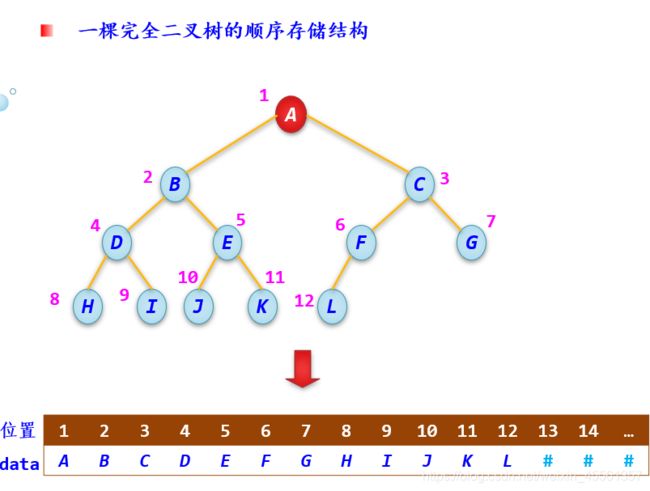
#include 通常将下标为0的位置空着,值为‘#’的结点为空结点。
链式结构
对于一般的二叉树,通常采用二叉链表示。
typedef struct tnode
{
ElemType data; //数据域
struct tnode *lchild,*rchild; //指针域
} BTNode;
//如果是叶子结点,则左右孩子指针为NULL
二叉链算法
#include 二叉树遍历
二叉树常用的遍历有先序(根)遍历、中序(根)遍历、后序(根)遍历和层次遍历。
基础知识
先序遍历:1.根结点 2.左孩子 3.右孩子
特点:其第一个元素值为二叉树中根结点值。
中序遍历:1.左孩子 2.根结点 3.右孩子
特点:若已知二叉树的根结点值,以该值为界,将中序遍历序列分为两部分,前半部分为左子树的中序遍历序列,后半部分为右子树的中序遍历序列。
后序遍历:1.左孩子 2.右孩子 3.根结点
特点:最后一个元素值为二叉树中根结点值。
实例
先序遍历:ABDECFG
中序遍历:DBEACGF
后序遍历:DEBGFCA
层次遍历:ABCDEFG
构造知识
二叉树的构造就是给定某些遍历序列,反过来唯一地确定该二叉树。



实例

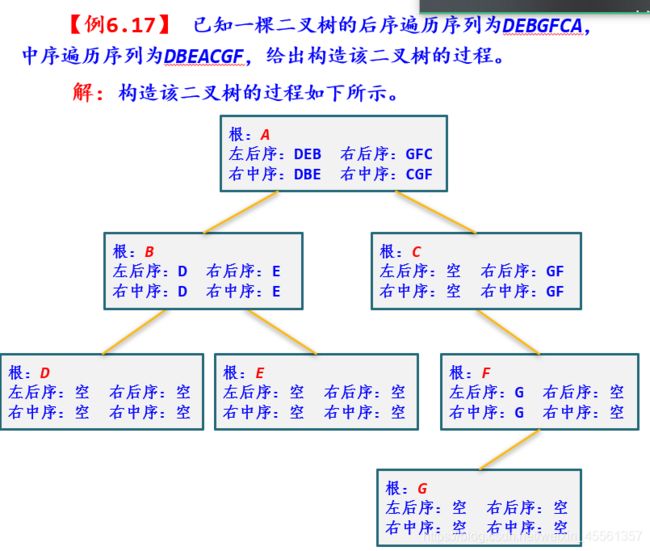
代码
/*先序遍历*/
void PreOrder(btnode *bt)
{
if (bt == NULL)
return;
else {
cout << bt->data << " ";
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
/*中序遍历*/
void InOrder(btnode *bt)
{
if (bt == NULL)
return;
else {
InOrder(bt->lchild);
cout << bt->data << " ";
InOrder(bt->rchild);
}
}
/*后序遍历*/
void PostOrder(btnode *bt)
{
if (bt == NULL)
return;
else {
PostOrder(bt->lchild);
cout << bt->data << " ";
PostOrder(bt->rchild);
}
}
/*层次遍历*/
void LevelOrder(btnode *bt)
{
btnode *p;
btnode *qu[maxsize]; //定义循环队列,存放二叉链结点指针
int front, rear; //定义队头和队尾指针
front = rear = 0; //置队列为空队列
rear++; qu[rear] = bt; //根结点指针进入队列
while (front != rear) //队列不为空循环
{
front = (front + 1) % maxsize;
p = qu[front]; //出队结点p
printf("%c ", p->data); //访问该结点
if (p->lchild != NULL) //有左孩子时将其进队
{
rear = (rear + 1) % maxsize;
qu[rear] = p->lchild;
}
if (p->rchild != NULL) //有右孩子时将其进队
{
rear = (rear + 1) % maxsize;
qu[rear] = p->rchild;
}
}
}
哈夫曼树
带权路径长度可能不相同。把其中具有最小带权路径长度的二叉树称为哈夫曼树。
根据哈夫曼树的定义,一棵二叉树要使其WPL值最小,必须使权值越大的叶子结点越靠近根结点。
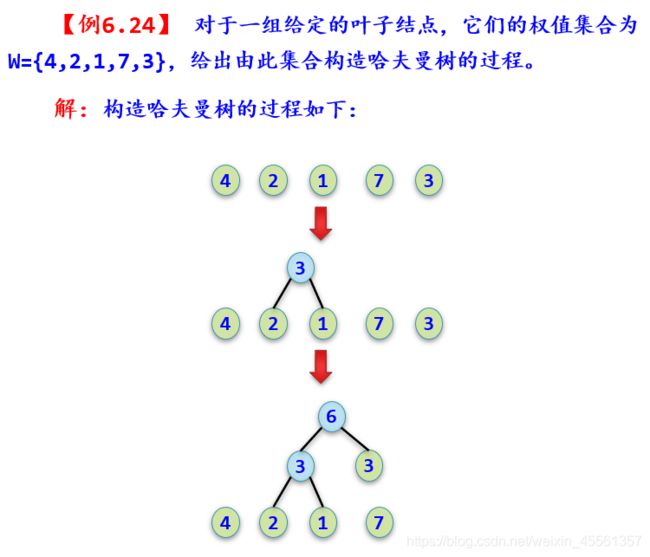
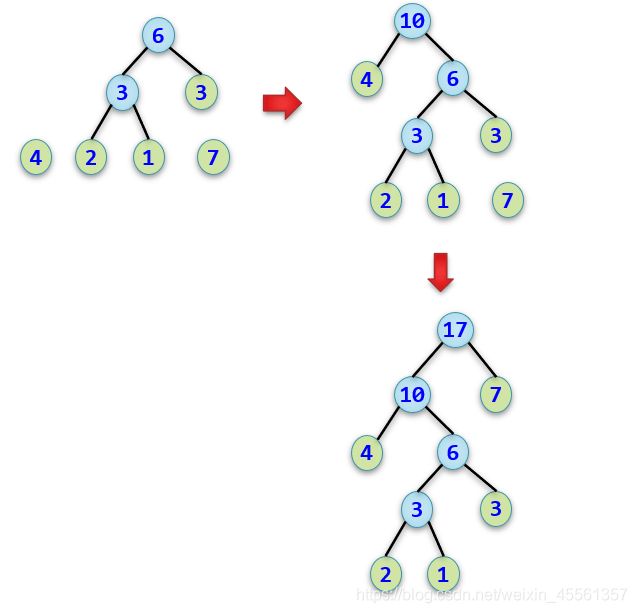
哈夫曼编码
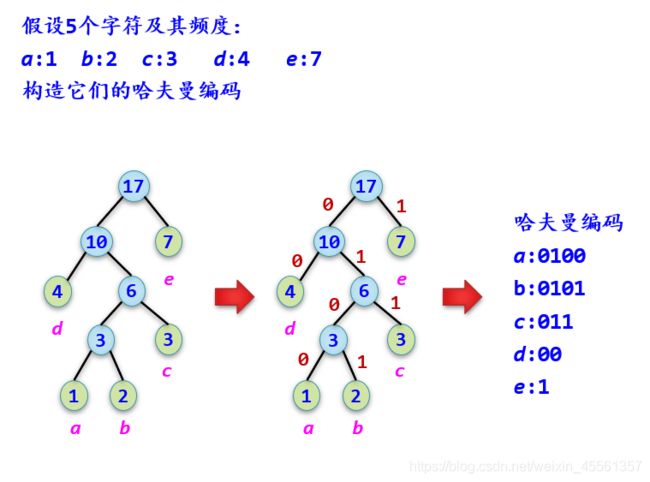
代码
/*实现哈夫曼树的创建算法,并按哈夫曼树实现哈夫曼编码算法。*/
#include