unity里的正交投影和透视投影

本文之前一直纠结的问题是unity里面的正交矩阵和透视矩阵中的z到底是映射到[-1,1]还是[0,1]区间。
经过验证之后，得出结论：
unity里的正交和透视矩阵是将z映射到[-1,1]区间。

经过查询，知道了，opengl把z映射到[-1,1]之间；而dx则将z映射到[0,1]区间。
可以查看：
https://knowledge.autodesk.com/search-result/caas/CloudHelp/cloudhelp/2017/ENU/Maya-SDK/files/GUID-3824AD22-F46C-4806-9884-2C6292468762-htm.html

有上面也知道了，dx是左手坐标系，而opengl是右手坐标系，而unity呢？我们会发现它使用的是左手坐标系。

左手坐标系、右手坐标系，下图可以直观的给出：

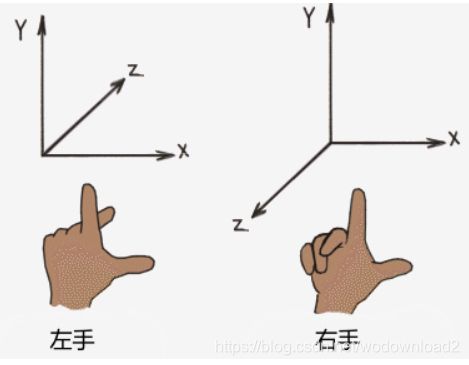
判定方法，摘自网络，原文如下：

1.左手坐标系: 伸开我们的左手, 掌心向外, 大拇指与食指成90度, 中指、无名指和小指弯曲, 大拇指指向的方向就是X轴正方向, 食指指向的方向就是Y轴正方向, 中指、无名指和小指指向的方向就是Z轴正方向。
2.右手坐标系: 伸开我们的右手, 掌心向内, 大拇指与食指成90度, 中指、无名指和小指弯曲, 大拇指指向的方向就是X轴正方向, 食指指向的方向就是Y轴正方向, 中指、无名指和小指指向的方向就是Z轴正方向。
3.左手坐标系和右手坐标系中, X轴和Y轴的方向是相同的, Z轴的方向相反。
--------------------- 
原文：https://blog.csdn.net/aihiao/article/details/80073477 

ok，了解了这么多，我们还要看下opengl的正交透视投影，以及透视投影的矩阵公式，推导这里就不要再叙述了，网上很多，我之前的博客也都写过，这里给出几个参考网址：
https://blog.csdn.net/popy007/article/details/1797121
https://blog.csdn.net/wangdingqiaoit/article/details/51589825
https://blog.csdn.net/wodownload2/article/details/52084300

这里还有一个不明白的地方就是在推导的时候，使用-N和-F。
还有一个地方不明的是，unity里面的摄像机的正方向，指向的是世界坐标系的-z轴。仿佛所有摄像机能看到的物体，都是在摄像机的后面。
有图说明：

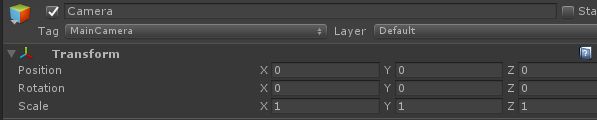
上图，camera的位置是(0,0,0)，其旋转为(0,0,0)，那么打印其worldToCameraMatrix，也就是世界坐标转换为视口坐标的矩阵。

Debug.Log(Camera.main.worldToCameraMatrix);

输出：

我们知道，凡是坐标系的矩阵的前三维代表的是xyz轴向量。
也就是摄像机的视口坐标系的三个轴是：
(1,0,0)
(0,1,0)
(0,0,-1)
由此知道，其z方向，和世界坐标系居然是相反的。
ok，这个只要知道就可以了，对我们的要验证的问题没有关系。

接着我们回到正交矩阵的验证问题上来：
首先，把z坐标映射到-1到1的正交投影矩阵公式如下：

我们来验证下：

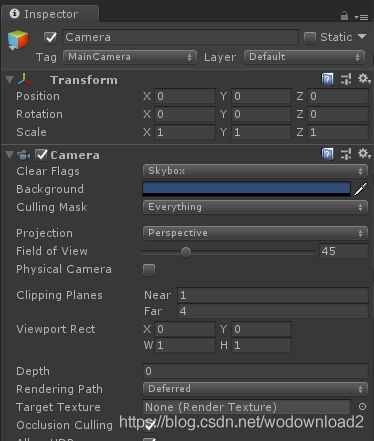
这里的摄像机其近平面设置为1，远平面设置为4，也就是n=1，f=4

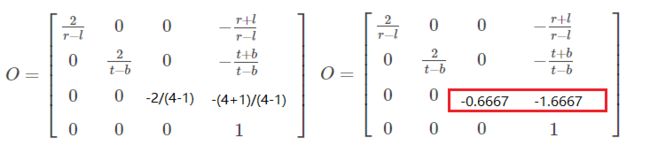
此时看下输出：

Debug.Log(Camera.main.projectionMatrix);

可以看到矩阵对第三行是验证正确。
再来看下矩阵的第一行和第二行。
当我们把另r=-l，以及t=-b的时候，
矩阵变为：

也就是：
1/r = 0.16667
1/t = 0.3333
此时r = 6，t = 3
这个是反推出r和t的。
ok，验证成立。

那么反思下，这个r和t的代表了什么，我们知道width=r-l=2r=12；而height=t-b=2t=6
那么此时宽高比是12:6=2:1,
那么此时我们的屏幕尺寸是多少呢？

 Debug.Log(Screen.width + "  " + Screen.height);
 Debug.LogError(Screen.height * 1.0f / Screen.width);
 Debug.LogError(Screen.width * 1.0f / Screen.height);

是的，我们屏幕的宽高比正好是2:1。
你可以选择，其他的分别测试：

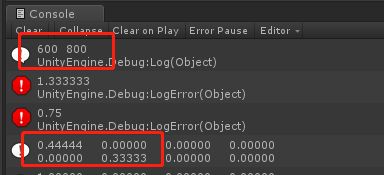
如屏幕是600x800，那么此时的比例是3:4=0.75，而0.3333/0.4444=0.75。验证是正确的。

我们再反思，我们的摄像机是正交的，那么屏幕的的比例，就是摄像机的宽高比。

下面要讲解的是如何将一个点映射到ndc空间了。
我们知道了给出了正交投影矩阵了，任何一个摄像机空间内的点p(x,y,z)，只要经过这个矩阵的变换，则最终都被映射到了[-1,1]的空间了。其中包括x和y和z。上面已经提到unity里面才用的是opengl的映射方式，将z映射到-1到1之间。

下面我们准备两个立方体：
立方体1

立方体2

摄像机

立方体1的坐标是(0,0,1)，立方体2的坐标是(0,0,4)，他们都是摄像机的子节点，而摄像机的坐标是(0,0,0)。
也就是立方体1的最终世界坐标是(0,0,1)，立方体2的最终坐标是(0,0,4)。

我们推测下，由于，摄像机的近平面是1，远平面是4，所以可以推测，立方体1的z=1，最终被映射到了-1，而立方体2的z=4，最终被映射到了1。
映射代码如下：

Debug.LogError(Camera.main.projectionMatrix.MultiplyPoint(Camera.main.worldToCameraMatrix.MultiplyPoint(cube.transform.position)));
Debug.LogError(Camera.main.projectionMatrix.MultiplyPoint(Camera.main.worldToCameraMatrix.MultiplyPoint(cube2.transform.position)));

其输出是：

推测争取。

下面，再来，我们试图将立方体1的y变为2，而立方体2的y变为-1，看其y轴映射对不对。
我们上面知道了摄像机的t=3，b=-3。
所以，推测立方体1的y，映射应该是2/3=0.6667
而立方体2的y，映射为-1/3=-0.3333

验证正确。

ok，至此unity里面的正交投影矩阵验证正确。

下面是验证透视投影矩阵了，我们把摄像机变为透视模式：

其属性设置为：

摄像机的近平面为1，远平面为4。
其投影矩阵为：

我们这里的n=1，f=4，r=-l， t=-b带入上面的矩阵：

输出：

可以看到第三行验证相同。
再来反推：t和r。
1/r = 3.21895，得到r=0.31
1/t = 2.41421，得到t=0.414
θ = 45度。
aspect = w/h = r/t，带入下面的公式，结果也是正确的。

下面就是验证z的映射是否争取了，我们另立方体1的z=1，立方体2的z=4，验证其投影映射之后的z值。

也就是说立方体1的z在近平面被映射为-1，而立方体2的z在远平面被映射为了1，结果正确。
其他关于x和y的映射带入也是满足的。

至此，unity中正交投影和透视投影的矩阵验证正确，网上推导的矩阵是真实可以用的。

最后给出项目的地址：