软阈值迭代算法(ISTA)和快速软阈值迭代算法(FISTA)
缺月挂疏桐,漏断人初静。
谁见幽人独往来,缥缈孤鸿影。
惊起却回头,有恨无人省。
拣尽寒枝不肯栖,寂寞沙洲冷。---- 苏轼
更多精彩内容请关注微信公众号 “优化与算法”
ISTA算法和FISTA算法是求解线性逆问题的经典方法,隶属于梯度类算法,也常用于压缩感知重构算法中,隶属于梯度类算法,这次将这2中算法原理做简单分析,并给出matlab仿真实验,通过实验结果来验证算法性能。
1. 引言
对于一个基本的线性逆问题:
y = A x + w ( 1 ) {\bf{y} = \bf{Ax} + \bf{w}} \quad \quad \quad \quad\quad \quad\quad \quad(1) y=Ax+w(1)
其中 A ∈ M × N {\bf{A }} \in {^{M \times N}} A∈M×N, y ∈ M {\bf{y }} \in {^{M}} y∈M且是已知的, w \bf{w} w是未知噪声。
(1)式可用最小二乘法(Least Squares)来求解:
x ^ L S = arg m i x n ∥ A x − y ∥ 2 2 ( 2 ) { {\bf{\hat x}}_{LS}} = \mathop {\arg {\mathop{\rm mi}\nolimits} }\limits_{\bf{x}} n\left\| { {\bf{Ax}} - {\bf{y}}} \right\|_2^2 \quad \quad \quad \quad\quad \quad\quad \quad(2) x^LS=xargmin∥Ax−y∥22(2)
当 M = N M=N M=N 且 A \bf{A} A 非奇异时,最小二乘法的解等价于 A − 1 y \bf{A^{-1}y} A−1y。
然而,在很多情况下, ( A ) \bf(A) (A) 是病态的(ill-conditioned),此时,用最小二乘法求解时,系统微小的扰动都会导致结果差别很大,可谓失之毫厘谬以千里,因此最小二乘法不适用于求解病态方程。
**什么是条件数?**矩阵 A \bf{A} A 的条件数是指 A \bf{A} A 的最大奇异值与最小奇异值的比值,显然条件数最小为1,条件数越小说明矩阵越趋于“良态”,条件数越大,矩阵越趋于奇异,从而趋于“病态”。
为了求解病态线性系统的逆问题,前苏联科学家安德烈·尼古拉耶维奇·吉洪诺夫提出了吉洪诺夫正则化方法(Tikhonov regularization),该方法也称为“岭回归”。最小二乘是一种无偏估计方法(保真度很好),如果系统是病态的,则会导致其估计方差很大(对扰动很敏感),吉洪诺夫正则化方法的主要思想是以可容忍的微小偏差来换取估计的良好效果,实现方差和偏差的一个trade-off。吉洪诺夫正则化求解病态问题可以表示为:
x ^ T = arg m i x n ∥ A x − y ∥ 2 2 + λ ∥ x ∥ 2 2 ( 3 ) { {\bf{\hat x}}_{T}} = \mathop {\arg {\mathop{\rm mi}\nolimits} }\limits_{\bf{x}} n\left\| { {\bf{Ax}} - {\bf{y}}} \right\|_2^2 + \lambda \left\| {\bf{x}} \right\|_2^2 \quad \quad \quad \quad\quad \quad\quad \quad(3) x^T=xargmin∥Ax−y∥22+λ∥x∥22(3)
其中 λ > 0 \lambda>0 λ>0 为正则化参数。问题(3)的解等价于如下岭回归估计器:
x ^ T = ( x T x + λ I ) − 1 x T y ( 4 ) { {\bf{\hat x}}_{T}} = {({ {\bf{x}}^{\rm T}}{\bf{x}} + \lambda {\bf{I}})^{ - 1}}{ {\bf{x}}^{\rm T}}{\bf{y}}\quad \quad \quad \quad\quad \quad\quad \quad(4) x^T=(xTx+λI)−1xTy(4)
安德烈·尼古拉耶维奇·蒂霍诺夫(俄文:阿尔瓦勒德普列耶娃;1906年10月17日至1993年10月7日)是苏联和俄罗斯数学家和地球物理学家,以对拓扑学、泛函分析、数学物理和不适定问题的重要贡献而闻名。他也是地球物理学中大地电磁法的发明者之一。
岭回归是采用 ℓ 2 {\ell _2} ℓ2 范数作为正则项,另一种求解式(1)的方法是采用 ℓ 1 {\ell _1} ℓ1 范数作为正则项,这就是经典的LASSO(Least absolute shrinkage and selection operator)问题:
x ^ = arg m i x n ∥ A x − y ∥ 2 2 + λ ∥ x ∥ 1 ( 5 ) {\bf{\hat x}} = \mathop {\arg {\mathop{\rm mi}\nolimits} }\limits_{\bf{x}} n\left\| { {\bf{Ax}} - {\bf{y}}} \right\|_2^2 + \lambda {\left\| {\bf{x}} \right\|_1}~~~~~~~~~~~~~~~~~~~~~~~~~(5) x^=xargmin∥Ax−y∥22+λ∥x∥1 (5)
采用 ℓ 1 {\ell _1} ℓ1 范数正则项相对于 ℓ 2 {\ell _2} ℓ2 范数正则项有两个优势,第一个优势是 ℓ 1 {\ell _1} ℓ1 范数正则项能产生稀疏解,第二个优势是其具有对异常值不敏感的特性,这一点恰好与岭回归相反。
式(5)中的问题是一个凸优化问题,通常可以转化为二阶锥规划(second order cone programming)问题,从而使用内点法(interior point)等方法求解。然而在大规模问题中,由于数据维度太大,而内点法的算法复杂度为 O ( N 3 ) O({N^3}) O(N3),导致求解非常耗时。
基于上述原因,很多研究者研究通过简单的基于梯度的方法来求解(5)式。基于梯度的方法其计算量主要集中在矩阵 A \bf{A} A 与向量 y \bf{y} y 的乘积上,算法复杂度小,而且算法结构简单,容易操作。
2. 迭代收缩阈值算法(ISTA)
在众多基于梯度的算法中,迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm)是一种非常受关注的算法,ISTA算法在每一次迭代中通过一个收缩/软阈值操作来更新 x \bf{x} x,其具体迭代格式如下:
x k + 1 = s o f t λ t ( x k − 2 t A T ( A x k − y ) ) ( 6 ) { { {\bf{x}}_{k + 1}} = { {\mathop{\rm soft}\nolimits} _{\lambda t}}({ {\bf{x}}_k} - 2t{ {\bf{A}}^{\rm T}}({\bf{A}}{ {\bf{x}}_k} - {\bf{y}}))}~~~~~~~~~~~~~~~~~~(6) xk+1=softλt(xk−2tAT(Axk−y)) (6)
其中 s o f t λ t ( ⋅ ) { {\mathop{\rm soft}\nolimits} _{\lambda t}}( \cdot ) softλt(⋅) 是软阈值操作函数:
s o f t T ( x ) = s i g n ( x i ) ( ∣ x i ∣ − T ) ( 7 ) { {\mathop{\rm soft}\nolimits} _T}({ {\bf{x}}_{\rm{}}}) = sign({x_i})(\left| { {x_i}} \right| - T)~~~~~~~~~~~~~~~~~~~~~~~~~~~(7) softT(x)=sign(xi)(∣xi∣−T) (7)
软阈值操作函数如下图所示:

其中 s i g n ( ) sign() sign() 是符号函数。
那么ISTA的迭代格式(6)式是怎么来的呢?算法中的“收缩阈值”体现在哪里?这要从梯度下降法(Gradient Descent)说起。
考虑一个连续可导的无约束最小化问题:
min { f ( x ) : x ∈ R N } ( 8 ) \min \{ f({\bf{x}}):{\bf{x}} \in {R^N}\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(8) min{ f(x):x∈RN} (8)
(8)式可用梯度下降法来求解:
x 0 ∈ R N , x k = x k − 1 − t k ∇ f ( x k − 1 ) ( 9 ) { {\bf{x}}_0} \in {R^N},~~~~~{ {\bf{x}}_k} = { {\bf{x}}_{k - 1}} - {t_k}\nabla f({ {\bf{x}}_{k - 1}})~~~~~~~~~~~~~~~~~(9) x0∈RN, xk=xk−1−tk∇f(xk−1) (9)
这里 t k > 0 t_k>0 tk>0 是迭代步长。我们知道,梯度下降法可以表示成 f f f 在点 x k − 1 x_{k-1} xk−1 处的近端正则化(proximal regularization),其等价形式可以表示为:
x k = arg m i x n { f ( x k − 1 ) + ⟨ x − x k − 1 , ∇ f ( x k − 1 ) ⟩ + 1 2 t k ∥ x − x k − 1 ∥ 2 2 } ( 10 ) { {\bf{x}}_k} = \mathop {\arg {\mathop{\rm mi}\nolimits} }\limits_{\bf{x}} n\left\{ {f({ {\bf{x}}_{k - 1}}) + \left\langle { {\bf{x}} - { {\bf{x}}_{k - 1}},\nabla f({ {\bf{x}}_{k - 1}})} \right\rangle + {1 \over {2{t_k}}}\left\| { {\bf{x}} - { {\bf{x}}_{k - 1}}} \right\|_2^2} \right\}~~~(10) xk=xargmin{ f(xk−1)+⟨x−xk−1,∇f(xk−1)⟩+2tk1∥x−xk−1∥22} (10)
(9)-(10)可由李普希兹连续条件 ∥ ∇ f ( x k ) − ∇ f ( x k − 1 ) ∥ 2 ≤ L ( f ) ∥ x k − x k − 1 ∥ 2 {\left\| {\nabla f({ {\bf{x}}_k}) - \nabla f({ {\bf{x}}_{k - 1}})} \right\|_2} \le L(f){\left\| { { {\bf{x}}_k} - { {\bf{x}}_{k - 1}}} \right\|_2} ∥∇f(xk)−∇f(xk−1)∥2≤L(f)∥xk−xk−1∥2 和 f f f 在 x k − 1 x_{k-1} xk−1 处的2阶泰勒展开得到,很简单,这里不再赘述。
将(8)式加上 ℓ 1 {\ell _1} ℓ1 范数正则项,得到:
min { f ( x ) + λ ∥ x ∥ 1 : x ∈ R N } ( 11 ) \min \{ f({\bf{x}}) + \lambda {\left\| {\bf{x}} \right\|_1}:{\bf{x}} \in {R^N}\} ~~~~~~~~~~~~~~~~~~~(11) min{ f(x)+λ∥x∥1:x∈RN} (11)
则(10)式相应变成:
x k = arg m i x n { f ( x k − 1 ) + ⟨ x − x k − 1 , ∇ f ( x k − 1 ) ⟩ + 1 2 t k ∥ x − x k − 1 ∥ 2 2 + λ ∥ x ∥ 1 } ( 12 ) { {\bf{x}}_k} = \mathop {\arg {\mathop{\rm mi}\nolimits} }\limits_{\bf{x}} n\left\{ {f({ {\bf{x}}_{k - 1}}) + \left\langle { {\bf{x}} - { {\bf{x}}_{k - 1}},\nabla f({ {\bf{x}}_{k - 1}})} \right\rangle + {1 \over {2{t_k}}}\left\| { {\bf{x}} - { {\bf{x}}_{k - 1}}} \right\|_2^2 + \lambda { {\left\| {\bf{x}} \right\|}_1}} \right\}~~(12) xk=xargmin{ f(xk−1)+⟨x−xk−1,∇f(xk−1)⟩+2tk1∥x−xk−1∥22+λ∥x∥1} (12)
时(12)忽略掉常数项 f ( x k − 1 ) f(\bf x_{k-1}) f(xk−1) 和 ∇ f ( x k − 1 ) {\nabla f({ {\bf{x}}_{k - 1}})} ∇f(xk−1) 之后,(12)式可以写成:
x k = s o f t λ t k ( x k − 1 − t k ∇ f ( x k − 1 ) ) ( 13 ) { {\bf{x}}_k} = { {\mathop{\rm soft}\nolimits} _{\lambda {t_k}}}({ {\bf{x}}_{k - 1}} - {t_k}\nabla f({ {\bf{x}}_{k - 1}})) ~~~~~~~~~~~~~~~~~~~~(13) xk=softλtk(xk−1−tk∇f(xk−1)) (13)
文献中已经证明,当迭代步长取 f f f 的李普希兹常数的倒数(即 1 L ( f ) {1 \over {L(f)}} L(f)1)时,由ISTA算法生成的序列 x k \bf x_k xk 的收敛速度为 O ( 1 k ) O({1 \over {\rm{k}}}) O(k1) ,显然为次线性收敛速度。
ISTA算法的伪代码见原文,matlab代码如下:
function [x_hat,error] = cs_ista(y,A,lambda,epsilon,itermax)
% Iterative Soft Thresholding Algorithm(ISTA)
% Version: 1.0 written by Louis Zhang @2019-12-7
% Reference: Beck, Amir, and Marc Teboulle. "A fast iterative
% shrinkage-thresholding algorithm for linear inverse problems."
% SIAM journal on imaging sciences 2.1 (2009): 183-202.
% Inputs:
% y - measurement vector
% A - measurement matrix
% lambda - denoiser parameter in the noisy case
% epsilon - error threshold
% inter_max - maximum number of amp iterations
%
% Outputs:
% x_hat - the last estimate
% error - reconstruction error
if nargin < 5
itermax = 10000 ;
end
if nargin < 4
epsilon = 1e-4 ;
end
if nargin < 3
lambda = 2e-5 ;
end
N = size(A,2) ;
error = [];
x_1 = zeros(N,1) ;
for i = 1:itermax
g_1 = A'*(y - A*x_1) ;
alpha = 1 ;
% obtain step size alpha by line search
% alpha = (g_1'*g_1)/((A*g_1)'*(A*g_1)) ;
x_2 = x_1 + alpha * g_1 ;
x_hat = sign(x_2).*max(abs(x_2)-alpha*lambda,0) ;
error(i,1) = norm(x_hat - x_1) / norm(x_hat) ;
error(i,2) = norm(y-A*x_hat) ;
if error(i,1) < epsilon || error(i,1) < epsilon
break;
else
x_1 = x_hat ;
end
end
实际过程中,矩阵 A \bf A A 通常很大,计算其李普希兹常数非常困难,因此出现了ISTA算法的Backtracking版本,通过不断收缩迭代步长的策略使其收敛。
3. 快速迭代收缩阈值算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA)
为了加速ISTA算法的收敛,文献中作者采用了著名的梯度加速策略Nesterov加速技术,使得ISTA算法的收敛速度从 O ( 1 k ) O({1 \over {\rm{k}}}) O(k1) 变成 O ( 1 k 2 ) O({1 \over {\rm{k^2}}}) O(k21)。具体的证明过程可参见原文的定理4.1。
FISTA与ISTA算法相比,仅仅多了个Nesterov加速步骤,以极少的额外计算量大幅提高了算法的收敛速度。而且不仅在FISTA算法中,在几乎所有与梯度有关的算法中,Nesterov加速技术都可以使用。那Nesterov加速技术为何如此神通广大呢?
Nesterov加速技术由大神Yurii Nesterov于1983年提出来的,它与目前深度学习中用到的经典的动量方法(Momentum method)很相似,和动量方法的区别在于二者用到了不同点的梯度,动量方法采用的是上一步迭代点的梯度,而Nesterov方法则采用从上一步迭代点处朝前走一步处的梯度。具体对比如下。
动量方法:
v t + 1 = u t v t − α t ∇ g ( θ t ) {v_{t + 1}} = {u_t}{v_t} - {\alpha _t}\nabla g({\theta _t}) vt+1=utvt−αt∇g(θt)
θ t + 1 = θ t + v t + 1 {\theta _{t + 1}} = {\theta _t} + {v_{t + 1}} θt+1=θt+vt+1
Nesterov方法:
v t + 1 = u t v t − α t ∇ g ( θ t + u t v t ) {v_{t + 1}} = {u_t}{v_t} - {\alpha _t}\nabla g({\theta _t} + {u_t}{v_t}) vt+1=utvt−αt∇g(θt+utvt)
θ t + 1 = θ t + v t + 1 {\theta _{t + 1}} = {\theta _t} + {v_{t + 1}} θt+1=θt+vt+1
对比可发现,Nesterov方法和动量方法几乎一样,只是梯度处稍有差别。下图能更直观看出二者的区别。
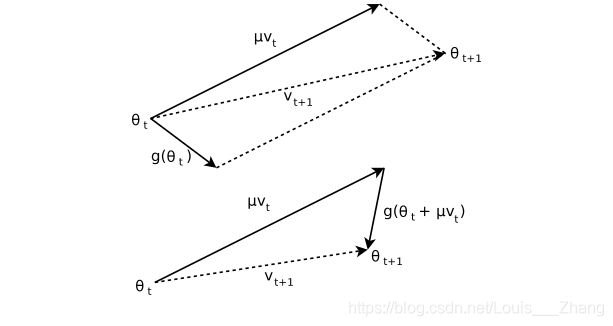
FISTA算法的伪代码见原文,matlab代码如下:
function [x_2,error] = cs_fista(y,A,lambda,epsilon,itermax)
% Fast Iterative Soft Thresholding Algorithm(FISTA)
% Version: 1.0 written by yfzhang @2019-12-8
% Reference: Beck, Amir, and Marc Teboulle. "A fast iterative
% shrinkage-thresholding algorithm for linear inverse problems."
% SIAM journal on imaging sciences 2.1 (2009): 183-202.
% Inputs:
% y - measurement vector
% A - measurement matrix
% lambda - denoiser parameter in the noisy case
% epsilon - error threshold
% inter_max - maximum number of amp iterations
%
% Outputs:
% x_hat - the last estimate
% error - reconstruction error
if nargin < 5
itermax = 10000 ;
end
if nargin < 4
epsilon = 1e-4 ;
end
if nargin < 3
lambda = 2e-5 ;
end
N = size(A,2);
error = [] ;
x_0 = zeros(N,1);
x_1 = zeros(N,1);
t_0 = 1 ;
for i = 1:itermax
t_1 = (1+sqrt(1+4*t_0^2))/2 ;
% g_1 = A'*(y-A*x_1);
alpha =1;
% alpha = (g_1'*g_1)/((A*g_1)'*(A*g_1)) ;
z_2 = x_1 + ((t_0-1)/(t_1))*(x_1 - x_0) ;
z_2 = z_2+A'*(y-A*z_2);
x_2 = sign(z_2).*max(abs(z_2)-alpha*lambda,0) ;
error(i,1) = norm(x_2 - x_1)/norm(x_2) ;
error(i,2) = norm(y-A*x_2) ;
if error(i,1) < epsilon || error(i,2) < epsilon
break;
else
x_0 = x_1 ;
x_1 = x_2 ;
t_0 = t_1 ;
end
end
4. 仿真实验
为了验证ISTA算法和FISTA算法的算法性能,此处用一维随机高斯信号做实验,测试程序如下:
% One-dimensional random Gaussian signal test script for CS reconstruction
% algorithm
% Version: 1.0 written by yfzhang @2019-12-8
clear
clc
N = 1024 ;
M = 512 ;
K = 10 ;
x = zeros(N,1);
T = 5*randn(K,1);
index_k = randperm(N);
x(index_k(1:K)) = T;
A = randn(M,N);
A=sqrt(1/M)*A;
A = orth(A')';
% sigma = 1e-4 ;
% e = sigma*randn(M,1);
y = A * x ;% + e ;
[x_rec1,error1] = cs_fista(y,A,5e-3,1e-4,5e3) ;
[x_rec2,error2] = cs_ista(y,A,5e-3,1e-4,5e3) ;
figure (1)
plot(error1(:,2),'r-');
hold on
plot(error2(:,2),'b-');
仿真结果图如下所示:
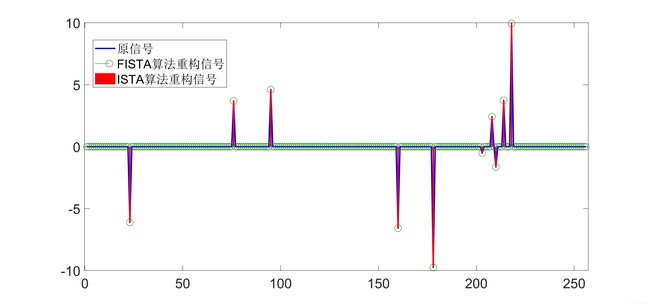
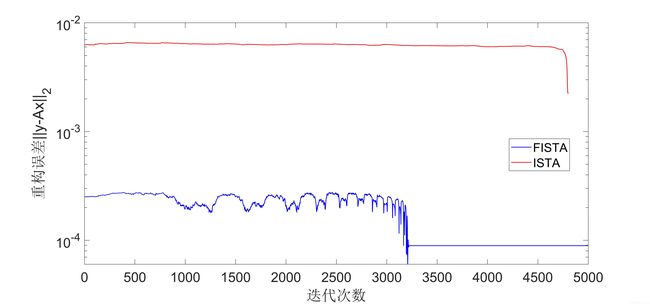
从实验结果可以看出,FIST算法收敛速度比ISTA算法要快很多。
这里顺便贴上原文中实验图,是关于图像去噪的:


图示为迭代次数与去噪效果的直观图,左边为FISTA算法,右边为ISTA算法,可以明显发现FISTA算法去噪速度较快。
5. 讨论
Iterative Shrinkage Thresholding 实际上不能称为一种算法,而是一类算法,ISTA算法和FISTA以及ISTA的改进算法如TWISTA算法等都是采用软阈值操作,求解的是 ℓ 1 {\ell _1} ℓ1 范数正则化问题(LASSO),而还有一些算法是采用硬阈值操作的,这类算法称为迭代硬阈值类算法(Iterative Hard Thresholding),这类算法求解的问题是 ℓ 0 {\ell _0} ℓ0 约束的最小化问题,是个非凸优化问题,以后有机会总结一下迭代硬阈值类算法。
参考文献
[1] Beck, Amir, and Marc Teboulle. “A fast iterative shrinkage-thresholding algorithm for linear inverse problems.” SIAM journal on imaging sciences 2.1 (2009): 183-202.
[2] Yurii E Nesterov., Dokl, akad. nauk Sssr. " A method for solving the convex programming problem with convergence rate O (1/k^ 2)" 1983.
往期文章链接:
最大比率发射(Maximum Ratio Transmission, MRT)
线性降维:主成分分析PCA原理分析与仿真验证
5G+AI:有哪些新的研究方向和新范式?
简述3D点云配准算法
5G为人工智能与工业互联网赋能|79页高清PPT
智能算法|以动物命名的算法
一份超全面的机器学习公共数据集
矩阵填充|奇异值阈值算法
可重构/大规模智能反射表面reconfigurable/large intelligent surface综述
迭代硬阈值类算法总结||IHT/NIHT/CGIHT/HTP
软阈值迭代算法(ISTA)和快速软阈值迭代算法(FISTA)
伍德伯里矩阵恒等式(Woodbury matrix identity)
压缩感知:一种新型亚采样技术
更多精彩内容请关注微信公众号 “优化与算法”


