并查集——带你手撕出代码,循序渐进,逐步优化
1.介绍:
在计算机科学中,并查集是一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。有一个联合-查找算法(Union-find Algorithm)定义了两个用于此数据结构的操作:
Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union:将两个子集合并成同一个集合。
由于支持这两种操作,一个不相交集也常被称为联合-查找数据结构(Union-find Data Structure)或合并-查找集合(Merge-find Set)。
为了更加精确的定义这些方法,需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素,称为代表,以表示整个集合。接着,Find(x) 返回 x 所属集合的代表,而 Union 使用两个集合的代表作为参数
2. 快速查找的并查集(quick find)

元素的id值一样,(这里是0 1)就代表他们在一个集合里面
显然查找id的时间复杂度是O(1)的,而在合并的时候需要遍历整个数组在这里是找到元素值为0/1的元素,修改成1/0。也就是将要合并元素的其中一个id换成另一个元素的id,具体看代码,很简单的
class UnionFind {
private:
int* id;
int count; //并查集中元素的个数
public:
UnionFind(int count){
this->count = count;
id = new int[count];
for (int i = 0; i < count; ++i)
id[i] = i;
}
~UnionFind(){
delete[] id;
}
int find(int p){
assert(p>=0 && p < count);
return id[p];
}
bool isConnected(int p,int q){
return find(p) == find(q);
}
void unionElements(int p,int q){
int pID = find(p);
int qID = find(q);
if(pID == qID)
return;
for (int i = 0; i < count; ++i)
if(id[i] == pID)
id[i] = qID;
}
};
3. 快速合并的并查集(quick union)

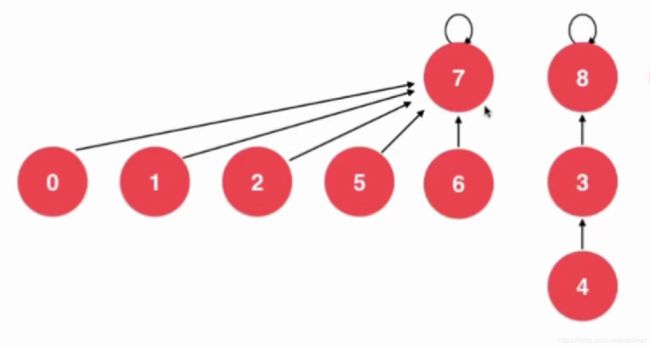
这次parent数组中记录的是他的父亲节点,初始的时候,我们让parent数组中的父亲节点都指向自己,也就是图中的环。
查找: 我们元素所在集合的时候都是去查找该元素的根节点,怎么找到他的根节点呢? 就是不断的往上查找父亲节点的过程,直到某个节点的父亲节点指向自己。
合并: 我们每次让其中一个元素的跟节点指向另一个元素的根节点就好了,所以合并的过程是很快的。
class UnionFind {
private:
int* parent;
int count; //元素的个数
public:
UnionFind(int count){
this->count = count;
parent = new int[count];
for (int i = 0; i < count; ++i)
parent[i] = i;
}
~UnionFind(){
delete[] parent;
}
int find(int p){
assert(p>=0 && p < count);
while(p != parent[p])
p = parent[p];
return p;
}
bool isConnected(int p,int q){
return find(p) == find(q);
}
void unionElements(int p,int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
parent[pRoot] = qRoot;
}
};
4. 再次优化
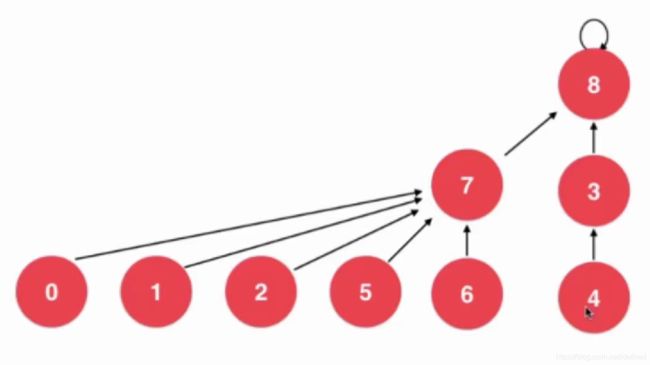
我们每次将高度更小的树,合并到另一颗树中。这样树的高度就没有那么高,那么当数据量特别大的时候,查找到的速度也会得到有效的提高。
rank[i] : 设定一个rank数组,rank数组的意思是根节点为i的树的高度。
而且想一想,只有当两个要合并的元素的根的rank值,也就是高度是一致的时候,我们才需要去维护rank数组。
代码:
class UnionFind {
private:
int* parent;
int* rank;
int count; //并查集中元素的个数
public:
UnionFind(int count){
this->count = count;
parent = new int[count];
rank = new int[count];
for (int i = 0; i < count; ++i) {
parent[i] = i;
rank[i] = 1;//初始时,高度为1,设置成0也是没问题的
}
}
~UnionFind(){
delete[] parent;
delete[] rank;
}
int find(int p){
assert(p>=0 && p < count);
while(p != parent[p])
p = parent[p];
return p;
}
bool isConnected(int p,int q){
return find(p) == find(q);
}
void unionElements(int p,int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
if(rank[pRoot] < rank[qRoot])
parent[pRoot] = qRoot;
else if(rank[pRoot] > rank[qRoot])
parent[qRoot] = pRoot;
else {
//rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot]++;
}
}
};
现在的处理速度已经非常可观了。
5. 路径压缩
思想: 我们每次查找的时候,将当前节点指向父亲节点的父亲节点。这样每次查找的时候,我们都将高度在减小,这就是路径压缩。

第一步: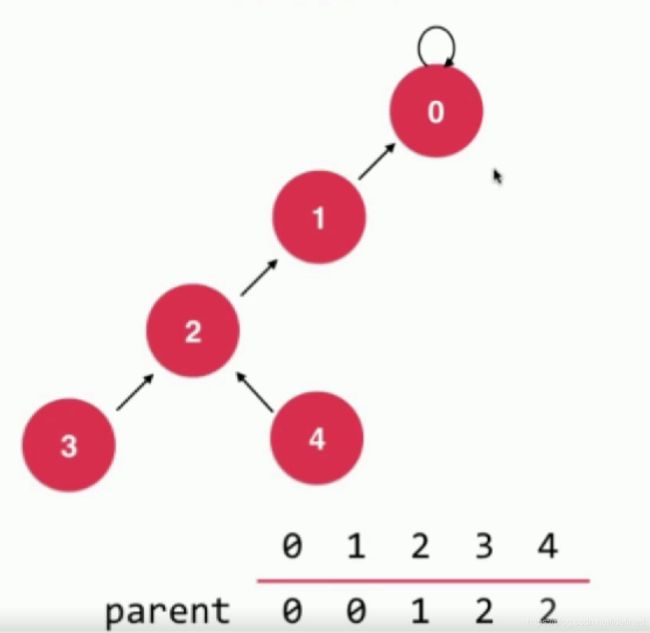
第二步
想一想其实这并不影响我们并查集的实现。因为,我们的目的就是为了找到某个元素的根节点,两个元素的根节点相同与否就决定了这两个元素是否在同一个集合当中。但是,当我们将路径压缩之后,我们树的高度进一步减小,那么查找的速度就会再次提高很多。整体的性能也会大大提升。
class UnionFind {
private:
int* parent;
int* rank;
int count; //并查集中元素的个数
public:
UnionFind(int count){
this->count = count;
parent = new int[count];
rank = new int[count];
for (int i = 0; i < count; ++i) {
parent[i] = i;
rank[i] = 1;//初始时,高度为1,设置成0也是没问题的
}
}
~UnionFind(){
delete[] parent;
delete[] rank;
}
int find(int p){
assert(p>=0 && p < count);
while(p != parent[p]) {
p = parent[parent[p]];
p = parent[p];
}
return p;
}
bool isConnected(int p,int q){
return find(p) == find(q);
}
void unionElements(int p,int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
if(rank[pRoot] < rank[qRoot])
parent[pRoot] = qRoot;
else if(rank[pRoot] > rank[qRoot])
parent[qRoot] = pRoot;
else {
//rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot]++;
}
}
};
尝试一道能利用并查集解决的问题 : 朋友圈
我的参考代码:
class Solution {
private:
int* parent;
int* rank;
int count;
public:
int find(int p){
while(p!= parent[p]){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
void unionElements(int q,int p){
int pRoot = find(p);
int qRoot = find(q);
if(qRoot == pRoot) return;
if(rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
} else if(rank[qRoot] > rank[pRoot]){
parent[pRoot] = qRoot;
}else{
parent[pRoot] = qRoot;
rank[pRoot]++;
}
}
int findCircleNum(vector<vector<int>>& M) {
int n = M.size();
this->count = n;
parent = new int[n];
rank = new int[n];
for (int i = 0; i < count; ++i) {
parent[i] = i;
rank[i] = 1;//树的高度
}
for (int i = 0; i < n; ++i)
for (int j = i+1; j < n; ++j) {
if(M[i][j] == 1)
unionElements(i,j);
}
vector<int> v = vector<int>(count,-1);
for (int k = 0; k < count; ++k) {
v[find(parent[k])] = 1;
}
int res = 0;
for (int l = 0; l < count; ++l) {
if(v[l] == 1)
res++;
}
return res;
}
~Solution(){
delete [] rank;
delete [] parent;
}
};
至此,结束。