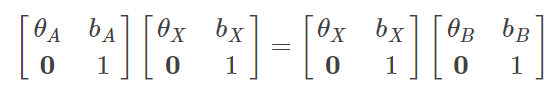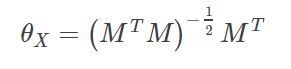手眼标定_全面细致的推导过程
本文解决的问题:
机械手搭载双目相机,手眼标定。
本文有细致的推导过程,非常全面。
文章目录
-
- 什么是手眼标定
- 为什么会存在这个?
- 相机的装载位置
-
- 不在手上(eye-to-hand)
- 在手上(eye-in-hand)
- 正式开始
- 验证结果
- 1. 基础坐标系(求解baseHtool)
- 2. camHcal相机到标定板
- 3. 求解AX=XB
-
- 李群李代数
- 利用李群知识求解AX=XB
-
- 求解旋转矩阵
- 求解平移向量
- 代码:用两组数据求解方程AX=XB
- 参考
什么是手眼标定
确定像素坐标系和空间机械手坐标系的坐标转化关系;
为什么会存在这个?
举一个生活中常见的例子——用手移动物体:
- 第一步:眼睛观察到三维世界,并将其转换到视网膜平面(三维空间转换到二维平面)传送信息给大脑;
- 第二步:大脑想要移动某个物体,假设想要将物体从A点移动B点(二维坐标),但是物体是三维空间中的物体,是三维坐标,需要将二维坐标换算成三维坐标;
- 第三步:大脑已经获得A点和B点的三维坐标,大脑给手(执行机构)发出指令去完成这个任务;
其中第二步就是手眼标定,得到二维坐标(像素坐标)到三维坐标的转换矩阵
在实际控制中,相机检测到目标在图像中的像素位置后,通过标定好的坐标转换矩阵将相机的像素坐标变换到机械手的空间坐标系中,然后根据机械手坐标系计算出各个电机该如何运动,从而控制机械手到达指定位置。这个过程中涉及到了图像标定,图像处理,运动学正逆解,手眼标定等。
相机的装载位置
不在手上(eye-to-hand)
相机固定在一个地方,机械手的运动不会带着相机一起移动。
在手上(eye-in-hand)
相机安装在机械手上,随着机械手一起移动。较为常用。这个实际上和eye-to-hand类似。
可以快速有效地标定被测物体的坐标。
这种情况的标定过程实际上和相机和机械手分离的标定方法是一样的,因为相机拍照时,机械手会运动到相机标定的时候的位置,然后相机拍照,得到目标的坐标,再控制机械手,所以简单的相机固定在末端的手眼系统很多都是采用这种方法,标定的过程和手眼分离系统的标定是可以相同对待的。
- 基于图像的视觉控制
- 基于位置的视觉控制
- 结合两者的混合视觉控制
在正式开始讲解之前,可以看一下博客:深入浅出地理解机器人手眼标定
对手眼标定有一个直观的认识。
正式开始
本文的相机搭载方案是,hand-in-eye。移动相机,标定求解过程
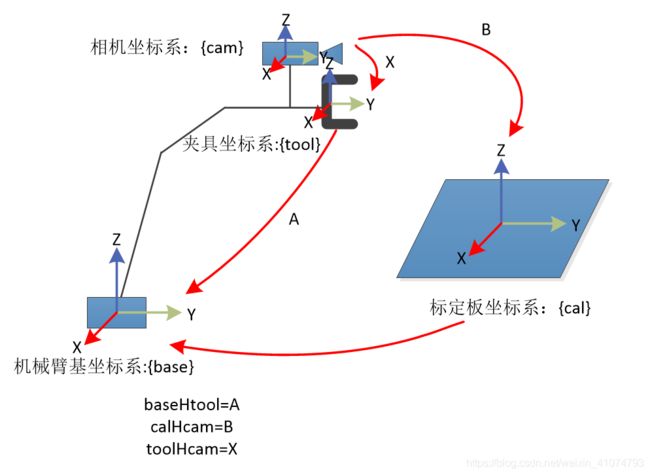
在推导过程中,我们会用到四个坐标系,分别是:
- 基础坐标系(用base表示)
- 机械手坐标系(用tool表示)
- 相机坐标系(用cam表示)
- 标定物坐标系(用cal表示)
- baseHtool:表示机械手坐标系到基础坐标系的转换关系,可以由机器人系统中得出。(已知)
- toolHcam:表示相机坐标系到机械手坐标系的转换关系;这个转化关系在机械手移动过程中是不变的;(未知,待求)
- calHcam:表示相机坐标系到标定板坐标系的转换关系(相机外參),可以由相机标定求出;(相当于已知)
- baseHcal:表示标定板坐标系到基础坐标系的变换,这个是最终想要得到的结果;只要机械手和标定板的相对位置不变,这个变换矩阵不发生变化。;
接下来控制机器手从初始位置移动到位置 1:
P b a s e = b a s e H t o o l ( 1 ) ∗ P t o o l ( 1 ) P_{base} =baseHtool (1)* P_{tool(1)} Pbase=baseHtool(1)∗Ptool(1)
P t o o l ( 1 ) = t o o l H c a m ∗ P c a m ( 1 ) P_{tool(1)} = toolHcam*P_{cam(1)} Ptool(1)=toolHcam∗Pcam(1)
P c a m ( 1 ) = c a l H c a m ( 1 ) − 1 ∗ P c a l P_{cam(1)}= calHcam(1)^{-1}*P_{cal} Pcam(1)=calHcam(1)−1∗Pcal
联合上面三个公式:
P b a s e = b a s e H t o o l ( 1 ) ∗ t o o l H c a m ∗ c a l H c a m ( 1 ) − 1 ∗ P c a l P_{base} = baseHtool (1)* toolHcam * calHcam(1)^{-1}*P_{cal} Pbase=baseHtool(1)∗toolHcam∗calHcam(1)−1∗Pcal
移动到机械手臂到位置2后:
P b a s e = b a s e H t o o l ( 2 ) ∗ t o o l H c a m ∗ c a l H c a m ( 2 ) − 1 ∗ P c a l P_{base} = baseHtool (2)* toolHcam * calHcam(2)^{-1}*P_{cal} Pbase=baseHtool(2)∗toolHcam∗calHcam(2)−1∗Pcal
因为base和obj是固定的,所以 b a s e H c a l baseHcal baseHcal不改变,所以:
b a s e H c a l = b a s e H t o o l ( 1 ) ∗ t o o l H c a m ∗ c a l H c a m ( 1 ) − 1 = b a s e H t o o l ( 2 ) ∗ t o o l H c a m ∗ c a l H c a m ( 2 ) − 1 \begin{aligned}baseHcal= &baseHtool (1)* toolHcam * calHcam(1)^{-1} \\ =&baseHtool (2)* toolHcam * calHcam(2)^{-1}\end{aligned} baseHcal==baseHtool(1)∗toolHcam∗calHcam(1)−1baseHtool(2)∗toolHcam∗calHcam(2)−1
记:
b a s e H t o o l ( 1 ) = A 1 , b a s e H t o o l ( 2 ) = A 2 baseHtool (1)=A_1,baseHtool (2)=A_2 baseHtool(1)=A1,baseHtool(2)=A2
t o o l H c a m = X toolHcam=X toolHcam=X
c a l H c a m ( 1 ) = B 1 , c a l H c a m ( 2 ) = B 2 calHcam(1)=B_1,calHcam(2)=B_2 calHcam(1)=B1,calHcam(2)=B2
所以:
A 1 ∗ X ∗ B 1 − 1 = A 2 ∗ X ∗ B 2 − 1 A_1*X*B_1^{-1}=A_2*X*B_2^{-1} A1∗X∗B1−1=A2∗X∗B2−1
A 2 − 1 ∗ A 1 ∗ X = X ∗ B 2 − 1 ∗ B 1 A_2^{-1}*A_1*X=X*B_2^{-1}*B_1 A2−1∗A1∗X=X∗B2−1∗B1
令 A 2 − 1 ∗ A 1 = A , B 2 − 1 ∗ B 1 = B A_2^{-1}*A_1=A , B_2^{-1}*B_1=B A2−1∗A1=A,B2−1∗B1=B
所以: A X = X B AX=XB AX=XB
所以:其中的A已知,X待求,B需要通过相机标定得知(张正友标定法可以求得)。
验证结果
公式: P b a s e = b a s e H t o o l ∗ t o o l H c a m ∗ c a l H c a m − 1 ∗ P c a l P_{base} = baseHtool * toolHcam * calHcam^{-1}*P_{cal} Pbase=baseHtool∗toolHcam∗calHcam−1∗Pcal
计: b a s e H c a l = b a s e H t o o l ∗ t o o l H c a m ∗ c a l H c a m − 1 baseHcal= baseHtool * toolHcam * calHcam^{-1} baseHcal=baseHtool∗toolHcam∗calHcam−1
所以: P b a s e = b a s e H c a l ∗ P c a l P_{base}=baseHcal*P_{cal} Pbase=baseHcal∗Pcal
b a s e H c a l baseHcal baseHcal是不变的,得到新的一组 b a s e H t o o l , c a l H c a m baseHtool,calHcam baseHtool,calHcam,带入 c a l H c c a m calHccam calHccam求解 b a s e H t o o l baseHtool baseHtool,判断两个 b a s e H t o o l baseHtool baseHtool是否相等。
最终想要得到的结果,系统的输入为: c a l H c c a m calHccam calHccam,输出是: b a s e H t o o l baseHtool baseHtool,这样机械手就能够运动到我们想要的位置了。
下面分为三个部分,分别讨论A、B、X的求解。
1. 基础坐标系(求解baseHtool)
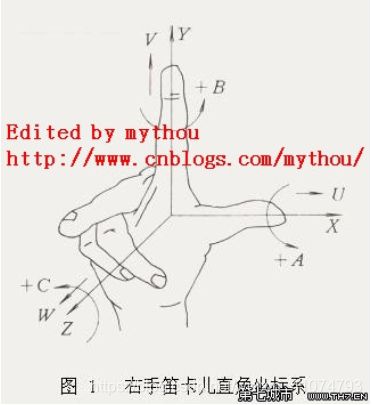
符合右手定则的XYZ三个坐标轴
六个自由度
-
三个位置:x、y、z(第六轴法兰盘圆心相对于原点的偏移量)
-
三个角:Rx、Ry、Rz(第六轴法兰盘的轴线角度,由初始姿态即竖直向上绕x轴旋转Rx度,再绕Y轴旋转Ry度,再绕Z轴旋转Rz度得到)
-
旋转方式(机器人RPY角和Euler角 – 基本公式)(机器人学-熊有伦36-40页)
-
绕定轴X-Y-Z旋转(判断机械臂输出四元数与代码得到的四元数是否相等得到)
- 旋转矩阵的计算方法如下: R = R z ∗ R y ∗ R x R = R_z* R_y *R_x R=Rz∗Ry∗Rx
(opencv的旋转方式是 z y x,所以旋转矩阵 R = R x ∗ R y ∗ R z R=Rx*Ry*Rz R=Rx∗Ry∗Rz)
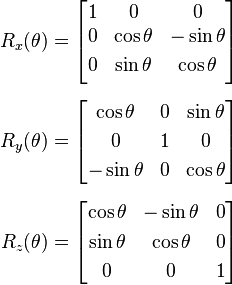
R = R x ∗ R y ∗ R z = X 1 Y 1 Z 3 R=R_x * R_y *R_z=X_1Y_1Z_3 R=Rx∗Ry∗Rz=X1Y1Z3

其中c为cos,s为sin。
所以: b a s e H t o o l = [ R t 0 1 ] baseHtool=\begin{bmatrix} R & t\\0 &1\end{bmatrix} baseHtool=[R0t1]
其中 t = [ x , y , z ] T t=[x,y,z]^T t=[x,y,z]T,从示教器读取
Rx、Ry、Rz分别是绕x、y、z轴的旋转角度。
(欧拉角-维基百科)
一定要注意欧拉角和李代数不一样,非常容易搞混,因为他们都是3个量 -
-
欧拉角:分别绕x、y、z轴旋转的角度,不一样的旋转次序,得到的R不一样;
-
李代数:维度是3,是绕一个轴转动一定的角度。欧拉角可以理解成李代数在x、y、z轴上的分解旋转。(不一定正确,不过比较形象)
注:不同机械臂示教器显示的法兰盘的数据格式不一样,有的是用欧拉角显示的,有的是用角轴显示的。
2. camHcal相机到标定板
- 注意:标定板坐标系下的坐标转换到相机坐标系下
思路大致如下:
- 已知双目相机的内参、畸变系数、外参( P r = R ∗ P l + t P_r=R*P_l+t Pr=R∗Pl+t),
- 对左右相机的两张图片调用OpenCV中的findChessboardCorners函数,找到内角点(如果结果不好,继续提取亚像素点);
- 将左右相机的像素点对应起来,得到匹配的2d点;
- 使用空间异面直线的方法,用对应的2d点计算出以右相机为世界坐标系的3维坐标 P c a m P_{cam} Pcam;(立体视觉匹配)
- 计算出每个角点以棋盘格为世界坐标的3维坐标 P c a l P_{cal} Pcal;
- 通过解方程 P c a m = c a m H c a l ∗ P c a l P_{cam}=camHcal*P_{cal} Pcam=camHcal∗Pcal求解出外参(3d-3d:ICP,SVD奇异值分解(十四讲173页))
张正友相机标定Opencv实现
findChessboardCorners函数
//! finds checkerboard pattern of the specified size in the image
CV_EXPORTS_W bool findChessboardCorners(
InputArray image,
Size patternSize,
OutputArray corners,
int flags=CALIB_CB_ADAPTIVE_THRESH+CALIB_CB_NORMALIZE_IMAGE );
参数解释:
- 第一个参数Image,传入拍摄的棋盘图Mat图像,必须是8位的灰度或者彩色图像;
- 第二个参数patternSize,每个棋盘图上内角点的行列数,一般情况下,行列数不要相同,便于后续标定程序识别标定板的方向;
- 第三个参数corners,用于存储检测到的内角点图像坐标位置,一般用元素是Point2f的向量来表示:vector image_points_buf;
- 第四个参数flage:用于定义棋盘图上内角点查找的不同处理方式,有默认值。
3. 求解AX=XB
以下四篇论文对应着四种求解方法
-
Tsai, Roger Y., and Reimar K. Lenz. “A new technique for fully autonomous and efficient 3D robotics hand/eye calibration.” IEEE Transactions on robotics and automation 5.3 (1989): 345-358.(博客:Tsai-Lenz的OpenCV实现)
-
Horaud, Radu, and Fadi Dornaika. “Hand-eye calibration.” The international journal of robotics research 14.3 (1995): 195-210.
-
Park, Frank C., and Bryan J. Martin. “Robot sensor calibration: solving AX= XB on the Euclidean group.” IEEE Transactions on Robotics and Automation10.5 (1994): 717-721.(博客:Navy的OpenCV实现)
-
Daniilidis, Konstantinos. “Hand-eye calibration using dual quaternions.” The International Journal of Robotics Research 18.3 (1999): 286-298.
网上有源代码可以下载:经典手眼标定算法C++代码
文献3采用的是李群的理论,将AX=XB转化成最小二乘问题;
文献4采用的时对偶四元数的知识,用对偶四元数表达旋转和平移,从而进行统一计算;
着四种算法精度差不多,不过文献4的效果要更好点。
具体实现文献3的算法,下面具体介绍
对数:乘法变加法
李群李代数
李代数到李群的转换满足指数映射关系,假设 [ w ] ∈ s o ( 3 ) [w]∈so(3) [w]∈so(3),而 e x p [ w ] ∈ S O ( 3 ) exp[w]∈SO(3) exp[w]∈SO(3),则其指数映射满足罗德里格斯公式:

其中 ∣ ∣ ω ∣ ∣ 2 = ω 1 2 + ω 2 2 + ω 3 2 ||\omega||^2=\omega_1^2+\omega_2^2+\omega_3^2 ∣∣ω∣∣2=ω12+ω22+ω32
(注意:正常的指数映射不是这种形式。)
利用李群知识求解AX=XB
展开得到:
θ A ∗ θ X = θ X ∗ θ B \theta_A*\theta_X=\theta_X*\theta_B θA∗θX=θX∗θB
θ A ∗ b X + b A = θ X ∗ b B + b X \theta_A*b_X+b_A=\theta_X*b_B+b_X θA∗bX+bA=θX∗bB+bX
采用“两步法”求解上述方程,先解算旋转矩阵,再求得平移向量。
求解旋转矩阵
假设 A X = X B AX=XB AX=XB,这里的都是旋转矩阵(SO(3)),并非变换矩阵(SE(3))。
变换可得到: A = X B X T A=XBX^T A=XBXT
两边取对数: l o g ( A ) = l o g ( X B X T ) log(A)=log(XBX^T) log(A)=log(XBXT)(对数映射)
令 l o g A = [ α ] , l o g B = [ β ] logA=[α],logB=[β] logA=[α],logB=[β],则上式可以化为
[ α ] = X [ β ] X T = [ X β ] [α]=X[β]X^T=[Xβ] [α]=X[β]XT=[Xβ],从而
α = X β α=Xβ α=Xβ
存在多组观测值时,求解该方程可以转化为下面最小二乘拟合问题:
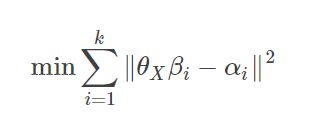
很显然,上述问题是典型的绝对定向问题,因而求解上式与绝对定向相同,其解为
然而,上式的求解是有条件的,即M不奇异,因而当A、B只有两组时,不能用上述方法求解。
当只有两组A、B时,即有 A 1 , A 2 , B 1 , B 2 A_1,A_2,B_1,B_2 A1,A2,B1,B2,
α 1 = l o g A 1 , α 2 = l o g A 2 , β 1 = l o g B 1 , β 2 = l o g B 2 α1=logA_1,α2=logA_2,β1=logB_1,β2=logB_2 α1=logA1,α2=logA2,β1=logB1,β2=logB2
θ X = M N − 1 θ_X=MN^{−1} θX=MN−1
其中, M = ( α 1 α 2 α 1 × α 2 ) M=(\begin{matrix}α1& α2 &α1×α2\end{matrix}) M=(α1α2α1×α2), N = ( β 1 β 2 β 1 × β 2 ) N=(\begin{matrix}β1 &β2&β1×β2\end{matrix}) N=(β1β2β1×β2), × \times ×表示叉乘。
即可求得旋转矩阵。
求解平移向量
θ A ∗ b X + b A = θ X ∗ b B + b X \theta_A*b_X+b_A=\theta_X*b_B+b_X θA∗bX+bA=θX∗bB+bX
移项化简得到:
( I − θ A ) ∗ b X = b A − ( θ X ∗ b B ) (I-\theta_A)*b_X=b_A-(\theta_X*b_B) (I−θA)∗bX=bA−(θX∗bB)
计作: c ∗ X = d c*X=d c∗X=d
又c不一定是可逆,所以两边同时乘以 c T c^T cT。即为: c T ∗ c ∗ X = c T ∗ d c^T*c*X=c^T*d cT∗c∗X=cT∗d
所以: X = ( c T ∗ c ) − 1 ∗ ( c T ∗ d ) X=(c^T*c)^{-1}*(c^T*d) X=(cT∗c)−1∗(cT∗d)
当有多组数据时:
( c 1 T ∗ c 1 + c 2 T ∗ c 2 + . . . + c n T ∗ c n ) ∗ X = c 1 T ∗ d 1 + c 2 T ∗ d 2 + . . . + c n T ∗ d n (c_1^T*c_1+c_2^T*c_2+...+c_n^T*c_n)*X \\=c_1^T*d_1+c_2^T*d_2+...+c_n^T*d_n (c1T∗c1+c2T∗c2+...+cnT∗cn)∗X=c1T∗d1+c2T∗d2+...+cnT∗dn
即可求得X,即平移向量
代码:用两组数据求解方程AX=XB
void camHtool_HandEye(std::vector<Eigen::Matrix4d> A,std::vector<Eigen::Matrix4d> B,
double cam_T_tool[4][4])
{
/*计算R*/
double alpha1[3], alpha2[3];
double beta1[3], beta2[3];
double A1[3][3], A2[3][3], B1[3][3], B2[3][3];
//A[1]本身是4*4的矩阵,函数只是取了前3*3的R
matrix2array_R(A[0], A1); //下标是从0开始的,不是从1开始,一开始写成了1;
matrix2array_R(A[1], A2);
matrix2array_R(B[0], B1);
matrix2array_R(B[1], B2);
my_RodriguesR2(A1, alpha1, 0);
my_RodriguesR2(A2, alpha2, 0);
my_RodriguesR2(B1, beta1, 0);
my_RodriguesR2(B2, beta2, 0);
double alpha1_2[3], beta1_2[3];
MyFunctionClass vision;
vision.my_Cross_Product(alpha1, alpha2, alpha1_2);
vision.my_Cross_Product(beta1, beta2, beta1_2);//值不对,已经改了,因为叉积哪里下标写成1开始
double M[3][3] = {
{
alpha1[0],alpha2[0],alpha1_2[0] },
{
alpha1[1],alpha2[1], alpha1_2[1]},
{
alpha1[2],alpha2[2], alpha1_2[2]} };
double N[3][3] = {
{
beta1[0], beta2[0], beta1_2[0]},
{
beta1[1], beta2[1], beta1_2[1]},
{
beta1[2], beta2[2], beta1_2[2] } };
double N_inv[3][3];
vision.my_Invert(N, N_inv);
double cam_R_tool[3][3];
vision.my_Times(M, N_inv, cam_R_tool);
/*计算平移t*/
double E_matrix[3][3];
vision.my_EyeMatrix(E_matrix);
double c1[3][3], c2[3][3];
vision.my_Minus(E_matrix, A1, c1); //c1=I-R_A1
vision.my_Minus(E_matrix, A2, c2);
double A1_t[3], A2_t[3], B1_t[3], B2_t[3];
matrix2array_t(A[0], A1_t);
matrix2array_t(A[1], A2_t);
matrix2array_t(B[0], B1_t);
matrix2array_t(B[1], B2_t);
//A1_t - (cam_R_tool*B1_t);
double temp_d1[3], temp_d2[3];
vision.my_Times(cam_R_tool, B1_t, temp_d1);
vision.my_Times(cam_R_tool, B2_t, temp_d2);
double d1[3], d2[3];
vision.my_Minus(A1_t, temp_d1, d1);
vision.my_Minus(A2_t, temp_d2, d2); //d1、d2
double c1_T[3][3], c2_T[3][3];
vision.my_Transpose(c1, c1_T);
vision.my_Transpose(c2, c2_T);
double c1_[3][3], c2_[3][3], C[3][3];
vision.my_Times(c1_T, c1, c1_);
vision.my_Times(c2_T, c2, c2_);
double d1_[3], d2_[3], D[3];
vision.my_Times(c1_T, d1, d1_);
vision.my_Times(c2_T, d2, d2_);
vision.my_Add(c1_, c2_, C);
vision.my_Add(d1_, d2_, D);
double C_inv[3][3];
vision.my_Invert(C, C_inv);
double cam_t_tool[3];
vision.my_Times(C_inv, D, cam_t_tool);
vision.R_t2T(cam_R_tool, cam_t_tool, cam_T_tool);
}
参考
- 深入浅出地理解机器人手眼标定
- 3D 视觉之手眼标定
- 经典手眼标定算法之Navy的OpenCV实现
- Eye-in-hand和Eye-to-hand问题求解和实验
- 机器人手眼标定(eye to hand和eye in hand)
- 手眼标定
- 手眼标定的两种方式
- Hand-Eye Calibration
- Hand-Eye Calibration Using Dual Quaternions