guided filter学习笔记

相关滤波器学习

Bilateral Filter

Bilateral Filter 为双边滤波, 其降噪效果在达到平滑降噪的功能的同时亦能保护边缘特征(edge-preserving). 这与他的滤波器的两个功能函数有关, 第一个便是空间核域函数, 这个函数通过欧氏距离来衡量每一个filter中各个像素与中心像素的距离来给每一个像素赋予权重; 第二个便是值域核函数, 这个函数通过对每一个filter中各个像素值与中心像素值的差值来对该filter中的每一个像素赋予权重.

在对Bilateral Filter的学习过程中, 借鉴了pan_jinquan博客的相关内容.

首先, 引用其他博主的关于对区域和边缘的理解, 如下:

我们都知道，一幅自然的图像可以被看成是有（过渡平缓的，也就是梯度较小）区域和（过渡尖锐的，也就是梯度较大）边缘（也包括图像的纹理、细节等）共同组成的。噪声是影响图像质量的不利因素，我们希望将其滤除。噪声的特点通常是以其为中心的各个方向上梯度都较大而且相差不多。边缘则不同，边缘相比于区域也会出现梯度的越变，但是边缘只有在其法向方向上才会出现较大的梯度，而在切向方向上梯度较小。

空间核函数

$$w_d^{i,j}(k,l)=exp(-\frac{(k-i{)}^2+(l-j{)}^2}{2{\sigma }^2})$$
在该数学函数式中, (i, j)为该filter的中心的坐标, (k, l)为filter中每一个像素点的坐标, $(k-i{)}^2+(l-j{)}^2$为该像素点与中心像素点的欧式空间距离, 下部的$\sigma$正态分布的标准差；

理解:在某一个filter中, 距离中心像素点越近, 其空间核函数的值越大; 反之, 距离中心像素点越远, 其空间核函数值越小. 在相对较平坦区域, 该函数其主要作用. 可以结合下图理解空间核函数.

值域核函数

$$w_r^{i,j}(k,l)=exp(-\frac{(f(k,l)-f(i,j){)}^2}{2{\sigma }^2})$$
在该数学函数式中, $f(i,j)$为该filter中心像素的值, $f(k,l)$为filter中周围的像素点的值.

理解: 在某一个filter中, 周围像素点的值与中心像素点的值越接近, $w_r$所给赋予该像素点的值域权重越大; 反之, 周围像素点的值与中心像素点的值相差越大, $w_r$所给赋予该像素点的值域权重越小. 这样的处理方式保证了在对边缘处理时的特征保留, 即在陡峭区域, 该函数起主要作用.

权值$w$

$$w_{i,j}(k,l)=w_d^{i,j}(k,l)\ast w_r^{i,j}(k,l)$$

应用模型

将应用模型分为三个部分, input_part§, process_part(箭头), output_part()q

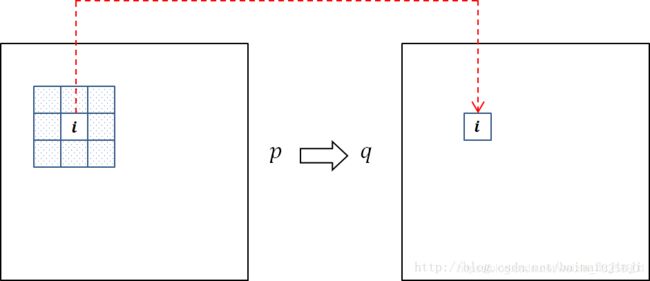
input_part

左图为输入部分, 我们想计算机输入一张图片, 假设该图片为$m\ast n$像素, 我们可以用一个矩阵来表示输入的内容:
$$inputContent=\left[\begin{array}{ccc}inpu{t}_{1,1}& \dots & inpu{t}_{1,n}\\ & & \\ \dots & inpu{t}_{i,j}& \dots \\ & & \\ inpu{t}_{m,1}& \dots & inpu{t}_{m,n}\end{array}\right]$$

output_part

右图为输出部分, 经过处理后, 计算机将输出一张和输入图片同尺寸的图片, 我们也用一个矩阵存储.
$$outputContent=\left[\begin{array}{ccc}outpu{t}_{1,1}& \dots & outpu{t}_{1,n}\\ & & \\ \dots & outpu{t}_{i,j}& \dots \\ & & \\ outpu{t}_{m,1}& \dots & outpu{t}_{m,n}\end{array}\right]$$

process_part

处理输入的数据, 输出处理后的数据, 便是process_part的功能, 具体处理过程如下:
将$inputContent$处理成一个$m\ast n\ast (t\ast t)$的矩阵$inputConten{t}^{\prime }$, 其元素$inputConten{t}_{i,j}^{\prime }$的值为$(n\ast n)$的矩阵,
$$outputConten{t}_{i,j}^{\prime }=\left[\begin{array}{ccc}inpu{t}_{i-\frac{n}{2},j-\frac{n}{2}}& \dots & inpu{t}_{i-\frac{n}{2},j}\\ & & \\ \dots & inpu{t}_{i,j}& \dots \\ & & \\ inpu{t}_{i+\frac{n}{2},j-\frac{n}{2}}& \dots & inpu{t}_{i+\frac{n}{2},j+\frac{n}{2}}\end{array}\right]$$
$$w_{i,j}=\left[\begin{array}{ccc}{w}_d^{i,j}(i-\frac{n}{2},j-\frac{n}{2})& \dots & w_d^{i,j}(i-\frac{n}{2},j)\\ & & \\ \dots & w_d^{i,j}(i,j)& \dots \\ & & \\ w_d^{i,j}(i+\frac{n}{2},j+\frac{n}{2})& \dots & w_d^{i,j}(i+\frac{n}{2},j+\frac{n}{2})\end{array}\right]$$
$$outpu{t}_{i,j}=w_{i,j}(.\ast )outputConten{t}_{i,j}^{\prime }$$
对每一个$outpu{t}_{i,j}$重复以上步骤, 便可得到output_part.

代码实现

Guided Filter

导向滤波与前者相比怎加了“导向”的这个概念, 在对$input$进行滤波的过程中, 引入了引导图$I$. 滤波的数学公式如下:
$$q_i=\sum _j{W}_{ij}(I)\cdot p_j$$
在这个公式中, $p_i$为$input$的第$j$个像素的值, $q_i$为$output$的第$i$个像素的值, 参数$W_{ij}(I)$是在引导图$I$的基础上的得出的.
Moreover, 该式子可以表达成以下的矩阵形式.
输出的矩阵为一个$j\ast 1$的矩阵.
$$q=\left[\begin{array}{ccc}{q}_1& \dots & q_j\end{array}\right]$$
输入的矩阵为一个$i\ast 1$的矩阵.
$$p=\left[\begin{array}{ccc}{p}_1& \dots & p_j\end{array}\right]$$
在处理的过程中$W(I)$矩阵便承担起了将输入数据转化为输出数据的任务.
$$W(I)=\left[\begin{array}{ccc}{W}_{1,1}(I)& \dots & W_{1,j}(I)\\ & & \\ \dots & & \dots \\ & & \\ W_{i,1}(I)& \dots & W_{ij}(I)\end{array}\right]$$
接下来我们的任务便是在已知guided image$I$的情况下, 将$W(I)$矩阵求出来.

$W_{ij}(I)$的求解过程

滤波器在滤波的过程中会将图片磨平, 而传统的滤波器在滤波的过程中容易受到图片区域的边界(陡峭部分)的影响, 会将边界当作需要磨平的区域, 进而将边界也磨平. 而这并不是我们所想要的结果, 于是, guided image便在此发挥的它的作用, 告诉滤波器那里是边界, 在边界的地方我们需要保留图片的边缘特征信息, 而不是将它磨平. 可以引用paper中的图片来理解这一过程.

在图片中, $q_i=p_i-n_i$可以看成滤波器降噪的过程, $n_i$是噪声; $q_i=a{I}_i+b$便是guided image发挥作用的过程.

由$q_i=a{I}_i+b$, 可以看出$q_i$和$I_i$之间是线性的, 所以对$a$和$b$的求解就显得非常重要了.

为了得到最适合的$a$和$b$, 依据无约束图像复原的方法, 优化目标是$minimize(n)$, 于是有
$$argmin\sum _i(q_i-p_i{)}^2$$
在求解此类问题, 通常采用最小二乘法的方法, 为了防止过拟合问题, 在loss function中添加惩罚项是有必要的, 优化目标函数如下:
$$E(a_k,b_k)=\sum _{i\in w_k}[(a_k{I}_i+h_k-p_i{)}^2+ϵa_k^2]$$
可得, 最终的优化结果为:
$$a_k=\frac{\frac{1}{|w|}{\sum }_{i\in w_k}{I}_i{p}_i-{\mu }_i\overline{p_k}}{{\sigma }_k^2+ϵ}$$
$$b_k=\overline{p_k}-a_k{\mu }_k$$
在式子中, ${\mu }_k$是guided image中第$k$个窗口$w_k$的平均值, ${\sigma }_K^2$是其方差, $|w|$为窗口$w_k$的像素数量, $\overline{p_k}$为input image $p$的窗口$w_k$的平均值.

在计算$q_i$时, 我们可以发现$output$的每一个像素会被多个filter给包含, 于是我们可以用每个像素的权重平均值来处理, 如下:
$$q_i=\frac{1}{|w|}\sum _{k:i\in w_k}(a_k{I}_i+b_k)=\overline{a_i}{I}_i+\overline{b_i}$$

式子中, $\overline{a_i}=\frac{1}{|w|}{\sum }_{k\in w_i}{a}_k$, $\overline{b_i}=\frac{1}{|w|}{\sum }_{k\in w_i}{b}_k$.

综上, 整个算法的流程下:

$Begin:$

$1st$, 计算$I$和$p$的每个窗口的平均值, 存入$meanOfL$和$meanOfP$中;

$2nd$, 计算$I$的方差和和$I-p$协方差, 存入$varOfL$和$covOfLP$中; 用于接下来的最小二乘法优化求解;

$3rd$, 最小二乘法优化求解, 求解出$a$和$b$;

$4th$, 求出$a$和$b$的中每个窗口的均值保存在$meanOfA$和$meanOfB$中;

$5th$, $q=meanofA.\ast L+meanOfB$

$End$

在以上的算法中, 出现了求一个image的每个窗口均值的过程, 在此处我们使用boxfilter的方法(后文附实现过程).

guided filter 代码实现

function q = guidedfilter(L, P, r, epsilon)
% L为guided image
% P为待处理的image
% r为filter的半径
% epsilon为最小二乘法中的惩罚参数

sizeOfFilter = boxfilter(ones(size(L)), r);
%% 1st
meanOfL = boxfilter(L, r) ./ sizeOfFilter;
meanOfP = boxfilter(P, r) ./ sizeOfFilter;
meanOfLtimeL = boxfilter(L .* L, r) ./ sizeOfFilter;
meanOfLtimeP = boxfilter(L .*P, r) ./ sizeOfFilter;

%% 2nd
% 在协方差计算公式中, 如果两个变量下相同, 计算结果便是该变量的方差
varOfL = meanOfLtimeL - meanOfL .* meanOfL;
% 协方差计算
covOfLP = meanOfLtimeP - meanOfL .* meanOfP;

%% 3rd
% 计算a的值
a = covOfLP ./ (varOfL + epsilon);
% 计算b的值
b = meanOfP - a .* meanOfL;

%% 4th
% a中每个filter的平均值
meanOfA = boxfilter(a, r) ./ sizeOfFilter;
% b中每个filter的平均值
meanOfB = boxfilter(b, r) ./ sizeOfFilter;

%% 5th
q = meanOfA .* L + meanOfB;

end

boxfilter

Boxfilter的初始化过程如下：
1、给定一张图像，宽高为（M,N），确定待求矩形模板的宽高(m,n)，如图紫色矩形。图中每个黑色方块代表一个像素，红色方块是假想像素。
2、开辟一段大小为M的数组，记为buff, 用来存储计算过程的中间变量，用红色方块表示
3、将矩形模板（紫色）从左上角（0，0）开始，逐像素向右滑动，到达行末时，矩形移动到下一行的开头（0，1），如此反复，每移动到一个新位置时，计算矩形内的像素和，保存在数组A中。以(0,0)位置为例进行说明：首先将绿色矩形内的每一列像素求和，结果放在buff内（红色方块），再对蓝色矩形内的像素求和，结果即为紫色特征矩形内的像素和，把它存放到数组A中，如此便完成了第一次求和运算。
4、每次紫色矩形向右移动时，实际上就是求对应的蓝色矩形的像素和，此时只要把上一次的求和结果减去蓝色矩形内的第一个红色块，再加上它右面的一个红色块，就是当前位置的和了，用公式表示 sum[i] = sum[i-1] - buff[x-1] + buff[x+m-1]
5、当紫色矩形移动到行末时，需要对buff进行更新。因为整个绿色矩形下移了一个像素，所以对于每个buff[i], 需要加上一个新进来的像素，再减去一个出去的像素，然后便开始新的一行的计算了。

boxfilter代码实现

function imDist = boxfilter_w_h(imSrc, r_w, r_h)

% imSrc 是待boxfilter处理的矩阵
% r_w, r_h 分别是窗口的x, y方向的半径
[hei, wid] = size(imSrc);
imCum = zeros(size(imSrc));
imDist = zeros(size(imSrc));

% 对y方向求窗口中心值累加
imCum = cumsum(imSrc, 1);
imDist(1: r_h + 1, :) = imCum(r_h + 1: 2 * r_h + 1, :);
imDist(r_h + 2: hei - r_h, :) = imCum(2 * r_h + 2: hei, :) - imCum(1: hei - 2 * r_h - 1, :);
imDist(hei - r_h + 1: hei, :) = repmat(imCum(hei, :), [r_h, 1]) - imCum(hei - 2 * r_h: hei - r_h - 1, :);

% 对x方向求窗口中心值累加
imCum = cumsum(imDist, 2);
imDist(:, 1: r_w + 1) = imCum(:, r_w + 1: 2 * r_w + 1);
imDist(:, r_w + 2: wid - r_w) = imCum(:, 2 * r_w + 2: wid) - imCum(:, 1: wid - 2 * r_w - 1);
imDist(:, wid - r_w + 1: wid) = repmat(imCum(:, wid), [1, r_w]) - imCum(:, wid - 2 * r_w: wid - r_w - 1);

end

e.g. 在guided filter中调用时使用的是$r_w$和$r_h$相等的boxfilter函数.

what’s more, fast-guided-filter

在guided filter的基础上, 我们引入采样率的概念, 假设采样率为s, guided filter的时间复杂度可以从原本的$O(N)$降低到$O(N/s^2)$. 而实现采样率的方法便是在原guided filter的算法前通过MATLAB中的imresize()将图像缩小$s^2$倍, 并在原guided filter算法的$5th$之前加上imresize()将图像放大原缩小倍数.

fast-guided-filter代码实现

function q = fastguidedfilter(L, P, r, epsilon, s)
% L 是guded image
% P 是输入的图像
% r是filter的半径大小
% epsilon是loss function的惩罚项
% s 是采样度

Ls = imresize(L, 1/s, 'nearest');
Ps = imresize(P, 1/s, 'nearest');
rs = r / s;

% sizeOfFilter保存每个filter的大小
sizeOfFilter = boxfilter(ones(size(Ls)), rs);
% meanOfLs保存L中每个filter的平均值
meanOfLs = boxfilter(Ls, rs) ./ sizeOfFilter;
meanOfPs = boxfilter(Ps, rs) ./ sizeOfFilter;
meanOfLsTimeLs = boxfilter(Ls .* Ls, rs) ./ sizeOfFilter;
meanOfLsTimePs = boxfilter(Ls .* Ps, rs) ./ sizeOfFilter;

% 协方差中两个变量若一样, 所得结果便是方差
varOfLs = meanOfLsTimeLs - meanOfLs .* meanOfLs;
% Ls和Ps的协方差
covOfLsPs = meanOfLsTimePs - meanOfLs .* meanOfPs;

% 最小二乘法求解参数a和b
a = covOfLsPs ./ (varOfLs + epsilon);
b = meanOfPs - a .* meanOfLs;

% 参数a的filter平均值
meanOfA = imresize(boxfilter(a, rs) ./ sizeOfFilter, size(L), 'bilinear');
% 参数b的filter平均值
meanOfB = imresize(boxfilter(b, rs) ./ sizeOfFilter, size(L), 'bilinear');

q = meanOfA .* L + meanOfB;

end

guided filter的应用

图像去雾应用

Single Image Haze Removal Using Dark Channel Prior

haze_rm 代码实现

clear
clc
close all
kenlRatio = 0.01;
minAtomsLight = 240;
% 图片路径
image_name =  './HFUT.JPG';
img=imread(image_name);
figure,imshow(uint8(img)), title('src');

sz=size(img);

w=sz(2);

h=sz(1);

dc = zeros(h,w);

for y=1:h

    for x=1:w

        dc(y,x) = min(img(y,x,:));

    end

end


figure,imshow(uint8(dc)), title('Min(R,G,B)');

krnlsz = floor(max([3, w*kenlRatio, h*kenlRatio]))

dc2 = minfilt2(dc, [krnlsz,krnlsz]);

dc2(h,w)=0;

figure,imshow(uint8(dc2)), title('After filter ');

t = 255 - dc2;

figure,imshow(uint8(t)),title('t');

t_d=double(t)/255;

sum(sum(t_d))/(h*w)


A = min([minAtomsLight, max(max(dc2))])

J = zeros(h,w,3);

img_d = double(img);

J(:,:,1) = (img_d(:,:,1) - (1-t_d)*A)./t_d;

J(:,:,2) = (img_d(:,:,2) - (1-t_d)*A)./t_d;

J(:,:,3) = (img_d(:,:,3) - (1-t_d)*A)./t_d;

figure,imshow(uint8(J)), title('J');
% figure,imshow(rgb2gray(uint8(abs(J-img_d)))), title('J-img_d');
% a = sum(sum(rgb2gray(uint8(abs(J-img_d))))) / (h*w)
% return;
%----------------------------------
r = krnlsz*4
eps = 10^-6;

% filtered = guidedfilter_color(double(img)/255, t_d, r, eps);
filtered = guidedfilter(double(rgb2gray(img))/255, t_d, r, eps);

t_d = filtered;

figure,imshow(t_d,[]),title('filtered t');

J(:,:,1) = (img_d(:,:,1) - (1-t_d)*A)./t_d;

J(:,:,2) = (img_d(:,:,2) - (1-t_d)*A)./t_d;

J(:,:,3) = (img_d(:,:,3) - (1-t_d)*A)./t_d;
% 

img_d(1,3,1)
imwrite(uint8(J),'./HFUT_haze_rm.jpg');
figure,imshow(uint8(J)), title('J_guild_filter');

%----------------------------------
%imwrite(uint8(J), ['_', image_name])

去雾实验

就地实验

今天恰好是个大雾天, 于是用手机拍了张雾天照片, 想着着试下模型的泛化性如何.

如上图, 左图为随手拍的雾天的照片, 右图为去雾后的照片. 发现效果不错, xixi.

于是接下来从原理上开始理解去雾的过程.
$1st$，
首先, 将RGB图的每个通道的最小值取出, 并保存到与原图同像素大小的单通道图中.
通过计算得到paper中 $A$ 的值为208.

$2nd$,
将上图通过之前学习的guided filter进行滤波, 得到paper中 $t$ , 如下图

$3rd$, 通过如下公式进行计算

便得到了去雾后的图片, 如下:

实验结果反思

倘若我们使用原始的minfilter进行滤波处理, 结果又会如何呢.

minfilter 代码实现

function Y = minfilt2(X,varargin)
%  MINFILT2    Two-dimensional min filter
%
%     Y = MINFILT2(X,[M N]) performs two-dimensional minimum
%     filtering on the image X using an M-by-N window. The result
%     Y contains the minimun value in the M-by-N neighborhood around
%     each pixel in the original image. 
%     This function uses the van Herk algorithm for min filters.
%
%     Y = MINFILT2(X,M) is the same as Y = MINFILT2(X,[M M])
%
%     Y = MINFILT2(X) uses a 3-by-3 neighborhood.
%
%     Y = MINFILT2(..., 'shape') returns a subsection of the 2D
%     filtering specified by 'shape' :
%        'full'  - Returns the full filtering result,
%        'same'  - (default) Returns the central filter area that is the
%                   same size as X,
%        'valid' - Returns only the area where no filter elements are outside
%                  the image.
%
%     See also : MAXFILT2, VANHERK
%

% Initialization
[S, shape] = parse_inputs(varargin{
     :});

% filtering
Y = vanherk(X,S(1),'min',shape);
Y = vanherk(Y,S(2),'min','col',shape);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [S, shape] = parse_inputs(varargin)
shape = 'same';
flag = [0 0]; % size shape

for i = 1 : nargin
   t = varargin{
     i};
   if strcmp(t,'full') & flag(2) == 0
      shape = 'full';
      flag(2) = 1;
   elseif strcmp(t,'same') & flag(2) == 0
      shape = 'same';
      flag(2) = 1;
   elseif strcmp(t,'valid') & flag(2) == 0
      shape = 'valid';
      flag(2) = 1;
   elseif flag(1) == 0
      S = t;
      flag(1) = 1;
   else
      error(['Too many / Unkown parameter : ' t ])
   end
end

if flag(1) == 0
   S = [3 3];
end
if length(S) == 1;
   S(2) = S(1);
end
if length(S) ~= 2
   error('Wrong window size parameter.')
end

minfilter 滤波对比

在使用minfilter的过程中, 在上面的$2nd$步骤, 和用guidedfilter便产生了差别.

如图所示, 左边是用guided filter处理得到的 $t$ 图像, 右边使用minfilter处理得到的图像.
中间过程的结果如是, 到了最终的输出的结果变因此产生了天翻地覆的差别, 如下所示:

在这个实例中, 我们也可以看出guided filter 在边缘处理的时候是发挥了很大的作用的. 就如同上图一样.