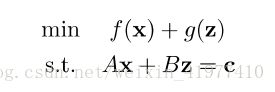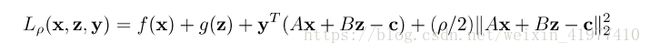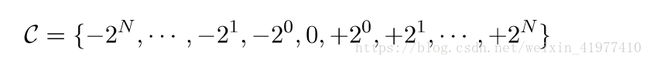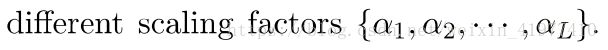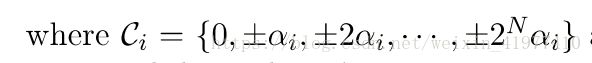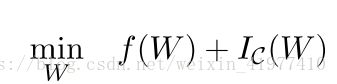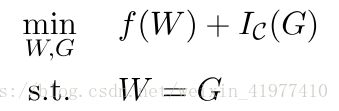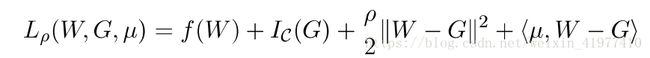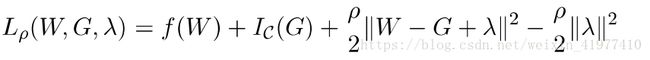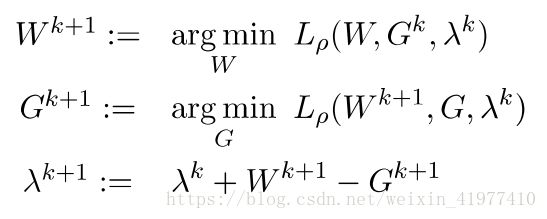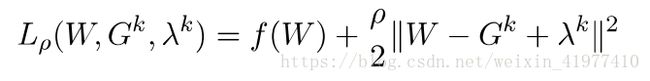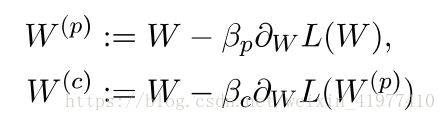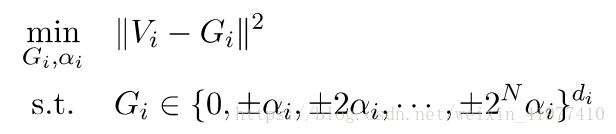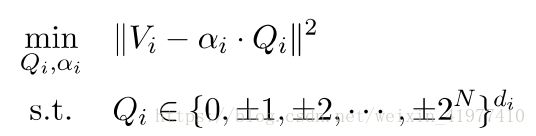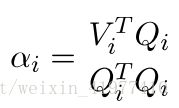【神经网络的压缩(第二弹)】Extremely Low Bit Nerual Network

主题：【神经网络的压缩(第二弹)】Extremely Low Bit Nerual Network

简介： 阿里巴巴团队提出来的低比特神经网络，被AAAI 2018收录为oral。2018年引用数不高，不过既然是深度学习压缩相关的文章，试着读读看一下。

附上论文链接：http://cn.arxiv.org/pdf/1707.09870v2

 

 

摘要：摘要部分总结来说就是深度学习模型已经被广泛应用于各种场景，但是对于计算能力和这个内存空间的要求也越来越高。那么为了能够压缩这个模型所占用的空间，提出了Extremely Low Bit Nerual Network 就是用最小的bit数来表示权值。这个问题被视作discretely constrained optimization  （离散约束优化问题）。然后通过ADMM算法得到了启发，将完整的问题分解成一个个小问题，然后通过extragradient and iterative quantization的方法来解决。论文的最后用大量的图像处理和目标检测的实验证明了这种算法的优越性。 这个图就是对整个压缩步骤的结构化解释，对摘要的一个形象化表示吧

一．Introduction

              CNN近年来在计算机视觉方面有很广泛的应用。随着网络的复杂化和深度化，需要存储的参数的量也越来越大（论文以16层的VGG为例，模型参数占据空间512M）。对计算和存储的极高要求成为了普及深度学习模型的障碍。为了能够让低端设备终端能够使用深度学习模型成为了对神经网络进行压缩的动力。

       接下来一段是对神经网络的压缩的各种算法进行了一个介绍。提到的论文稍后我会去搜一下然后附上链接。这篇论文在这里梳理的是比较清楚的，不出意外会沿着这个思路走一下。

https://en.wikipedia.org/wiki/Integer_programming

吹了一波ADMM算法，趁机去了解了一波：

介绍了论文的主要内容：介绍了怎样将连续的参数离散化来减少参数存储需要的比特数。

通过ADMM算法来将完整的问题分割成proximal step, projection step, dual step的三个步骤。然后通过不同的方法分别来解决这些问题proximal step（extragradient）, projection step(迭代量化), dual step/

二．Related Work

       这一段主要是对神经网络的低比特量化的方法做了一个简单的review。

···      2.1 神经网络的低比特量化

简单来说从1990年看手机就有人研究这玩意了，只不过当年的神经网络很浅所以没有办法证明压缩效果。二值化和三值化权重的方法被人翻来覆去研究过很多遍了，BibaryConnect就是其中的代表，这种方法将权重W 转化为sign（W）。但是这种方法在ImageNet数据集方面性能严重下滑。人们为了改进BibaryConnect方法，提出了BWN和TWN(是为了避免剃度为0)。

都让开重点来了： 和之前的这些研究不同，这篇论文将低比特量化问题指定为一个离散的约束问题并且提出一个基于ADMM的统一框架，并在离散和连续空间上进行模拟。。

 

2.2 啥是ADMM

Alternating Direction Method of Multipliers 交替方向乘子法

吸取了对偶上升法的可分解性和拉格朗日乘子法的收敛性的优势。

下面公式展示的是ADMM算法可以解决什么样的优化问题：

 

增广拉格朗日乘子法求解上述约束问题：

相比较一般的拉格朗日乘子法而言，多了一个二阶的惩罚项

Y就是拉格朗日乘子，因为引入了变量y,原问题转化成了对偶问题。

ADMM包含三步迭代：

前两步迭代就是在控制拉格朗日乘子不改变，然后求解min Lp，然后再控制x，z不变，更新y的直至收敛，这一部分的解释参考了

知乎：https://www.zhihu.com/question/36566112/answer/79535746的回答：

 

 

三．The proposed Method

定义 fW为神经网络的损失函数，W=W1,W2,……WL,Wi是第i层神经网络的权重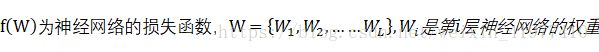

以卷积神经网络为例，在卷积层就是一个四维的张量，在全量阶层表示的就是一个二维的矩阵。，为了方便论述，

PS： 论文中将神经网络的权值限制为0或者2的幂，为的是能够用简单的位移操作来替代原本的浮点数的乘法

3.1 objective function

举例说明：加入神经网络的权值为 0，-1，+1，即三元神经网络，那么神经网络的训练过程就变成了：

同理可得，若权值设定为2的幂，则：

设置scaling因子，α>0,同时，α的值在神经网络的不同层取不同的值：

PS:每一层的α不会引起额外的卷积计算量

于是神经网络的训练就变成了如下过程：

3.2 Deouple with ADMM

在之前的研究中很多人尝试直接训练低比特模型来求最小的loss。例如BinaryConnect中将权值W替换为sign（W）(将权值转化为0，+1，-1) ，由于sign（）的导数处处为0，所以提出了hard tanh函数来替代sign()

论文中突破性的尝试了非凸优化技术 即ADMM：、

• 定义指示函数Ic(),上文提到的优化问题可以写为：

• . 设置辅助变量重写上述方程

• 结合上文提到的ADMM算法：μ是拉格朗日算子，<>求内积i

======》

• 结合ADMM算法的解法：这三步迭代分别为proximal step, projection step, dual step

由于摆脱了约束条件，所以每一步的求解可以使用梯度下降法

 

3.3 Algorithm subtroutines(算法的分布详解)

 

Ⅰproximal step

 

找到下列函数的最小值：

 

如果通过标准的梯度下降法，对W求导可以得到下式，但是这么做loss函数不能得到充分的优化（次优化方案），因为随着第二项的比重在loss中越来越大，收敛速度开始变慢。

 

为了克服这个问题，使用extragradient 方法：

extragradient 方法的一轮迭代分为两部（prediction  correction）

 

PS：第一步可以使得而二次正则化项消失，第二步则求解loss的最小值

优点是能够避免loss函数收敛在局部最小值。

 

 

紧接着我们来考虑散步迭代的第二个式子：每一层的辅助变量Gi可以独立优化

所以我们将权重W和拉格朗日乘子λ看作一个整体V,寻找V在离散集C上的投影

 

将扩展因子α单独拿出来

通过控制其中一个变量，优化另一个变量的迭代量化方法，可以得出：

在大多数情况下，继续最多五次迭代就可以得到一个稳定的结果

 

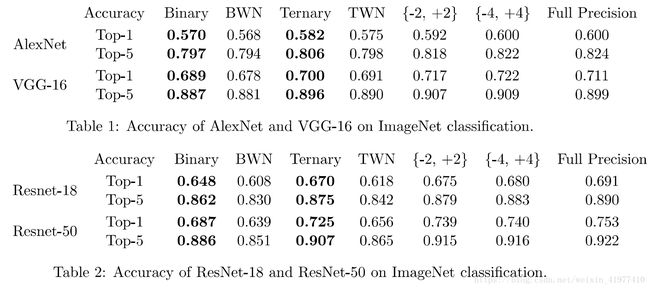
四．Experiment

   为了能够证实算法的性能，使用的是ImageNet 数据集来进行图片分类，同时作为对照实验，选择了广为应用的卷积神经网络中的代表模型 AlexNet,VGG-16,resNer-8，ResNet-50