TensorFlow 2.0深度学习算法实战 第七章 反向传播算法

The longer you can look back, the farther you can look forward. - 丘吉尔

第 6 章我们已经系统地介绍完基础的神经网络算法：从输入和输出的表示开始，介绍感知机的模型，介绍多输入、多输出的全连接网络层，然后扩展至多层神经网络；介绍了针对不同的问题场景下输出层的设计，最后介绍常用的损失函数，及实现方法。

本章我们将从理论层面学习神经网络中的核心算法之一：反向传播算法(Backpropagation，BP)。实际上，反向传播算法在 1960 年代早期就已经被提出，然而并没有引起业界重视。1970 年，Seppo Linnainmaa 在其硕士论文中提出了自动链式求导方法，并将反向传播算法实现在计算机上。1974 年，Paul Werbos 在其博士论文中首次提出了将反向传播算法应用到神经网络的可能性，但遗憾的是，Paul Werbos 并没有后续的相关研究发表。实际上，Paul Werbos 认为，这种研究思路对解决感知机问题是有意义的，但是由于人工智能寒冬，这个圈子大体已经失去解决那些问题的信念。直到 10 年后，1986 年，Geoffrey Hinton 等人在神经网络上应用反向传播算法 (Rumelhart, Hinton, & Williams,1986)，使得反向传播算法在神经网络中焕发出勃勃生机。

有了深度学习框架自动求导、自动更新权值的功能，算法设计者几乎不需要对反向传播算法有深入的了解也可以搭建复杂的模型和网络，通过优化工具方便地训练网络模型。但是反向传播算法和梯度下降算法是神经网络的核心算法，深刻理解其工作原理十分重要。我们先回顾导数、梯度等数学概念，然后推导常用激活函数、损失函数的梯度形式，并开始逐渐推导感知机、多层神经网络的梯度传播方式。

7.1 导数与梯度

在高中阶段，我们就接触到导数(Derivative)的概念，它被定义为自变量在$x_0$处产生一个微小扰动∆后，函数输出值的增量∆与自变量增量∆的比值在∆趋于 0 时的极限，如果存在，即为在0处的导数:
$$a=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(x+x_0\right)-f(x)}{\Delta x}$$

函数的导数可以记为$f^{\prime }(x)$或$\frac{dy}{dx}$。从几何角度来看，一元函数在某处的导数就是函数的切线在此处的斜率，函数值沿着方向的变化率。考虑物理学中例子：自由落体运动的位移函
数的表达式$y=\frac{1}{2}g{t}^2$，位移对时间的导数$\frac{dy}{dt}=\frac{d\frac{1}{2}g{t}^2}{dt}=gt$，考虑到速度定义为位移的变化率，因此 = gt，位移对时间的导数即为速度。

实际上，(方向)导数是一个非常宽泛的概念，只是因为我们以前接触到的函数大多是一元函数，自变量∆只有 2 个方向：+，−。当函数的自变量大于一个时，函数的导数拓展为函数值沿着任意∆方向的变化率。导数本身是标量，没有方向，但是导数表征了函数值在某个方向∆的变化率。在这些任意∆方向中，沿着坐标轴的几个方向比较特殊，此时的导数也叫做偏导数(Partial Derivative)。对于一元函数，导数记为$\frac{dy}{dx}$；对于多元函数的偏导数，记为$\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},\dots$等。偏导数是导数的特例，也没有方向。

考虑为多元函数的神经网络模型，比如 shape 为[784, 256]的权值矩阵 W，它包含了784×256 个连接权值，我们需要求出 784*256 个偏导数。需要注意的是，在数学公式中，我们一般要讨论的自变量是，但是在神经网络中，一般用来表示输入，比如图片，文本，语音数据等，网络的自变量是网络参数集 = {1, 1, 2, 2, … }，我们关心的也是误差对网络参数的偏导数 $\frac{\partial \mathcal{L}}{\partial w_1},\frac{\partial \mathcal{L}}{\partial b_1}$等。它其实就是函数输出ℒ沿着某个自变量变化方向上的导数，即偏导数。利用梯度下降算法优化网络时，需要求出网络的所有偏导数。我们把函数所有偏导数写成向量形式：
$$\nabla \mathcal{L}=\left(\frac{\partial \mathcal{L}}{\partial {\theta }_1},\frac{\partial \mathcal{L}}{\partial {\theta }_2},\frac{\partial \mathcal{L}}{\partial {\theta }_3},\dots \frac{\partial \mathcal{L}}{\partial {\theta }_n}\right)$$
此时梯度下降算法可以按着向量形式进行更新：
$${\theta }^{\prime }=\theta -\eta \ast \nabla \mathcal{L}$$
梯度下降算法一般是寻找函数的最小值，有时希望求解函数的最大值，如增强学习中希望最大化奖励函数，则可按着梯度方向更新
$${\theta }^{\prime }=\theta +\eta \ast \nabla \mathcal{L}$$
即可，这种方式的更新称为梯度上升算法。其中向量$\left(\frac{\partial \mathcal{L}}{\partial {\theta }_1},\frac{\partial \mathcal{L}}{\partial {\theta }_2},\frac{\partial \mathcal{L}}{\partial {\theta }_3},\dots \frac{\partial \mathcal{L}}{\partial {\theta }_n}\right)$叫做函数的梯度(Gradient)，它由所有偏导数组成，表征方向，梯度的方向表示函数值上升最快的方向，梯度的反向表示函数值下降最快的方向。

通过梯度下降算法并不能保证得到全局最优解，这主要是目标函数的非凸性造成的。考虑图 7.1 非凸函数，深蓝色区域为极小值区域，不同的优化轨迹可能得到不同的最优数值解。

神经网络的模型表达式非常复杂，模型参数量可达千万、数亿级别，几乎所有的神经网络的优化问题都是依赖于深度学习框架去自动计算每层的梯度，然后采用梯度下降算法循环迭代优化网络的参数直至性能满足需求。

在介绍多层神经网络的反向传播算法之前，我们先介绍导数的常见属性，常见激活函数、损失函数的梯度推导，然后再推导多层神经网络的梯度传播规律。

7.2 导数常见性质

本节介绍常见的求导法则和样例，为神经网络函数求导铺垫。

7.2.1 基本函数的导数

❑ 常数函数 c 导数为 0，如 = 2函数导数′ = 0

❑ 线性函数 = ∗ + 导数为，如函数 = 2 ∗ + 1导数′ = 2

❑ 幂函数$x^a$导数为 ∗ $x^{a-1}$，如 = $x^2$函数′ = 2 ∗

❑ 指数函数$a^x$ 导数为 ∗ ，如 =$e^x$函数′ = $e^x$ ∗ = $e^x$

❑ 对数函数${\log }_{a}x$导数为 $\frac{1}{x\ln a}$，如 = 函数′ = $\frac{1}{x\ln e}$

7.2.2 常用导数性质

❑ 函数加减 ( + )′ = ′ + ′

❑ 函数相乘 ()′ = ′ ∗ + ∗ ′

❑ 函数相除 ${\left(\frac{f}{g}\right)}^{\prime }=\frac{f^{\prime }g-f{g}^{\prime }}{g^2},g\ne 0$

❑ 复合函数的导数 考虑复合函数(())，令 = ()，其导数
$$\frac{df(g(x))}{dx}=\frac{df(u)}{du}\frac{dg(x)}{dx}=f^{\prime }(u)\ast g^{\prime }(x)$$

7.2.3 导数求解实战

考虑目标函数$\mathcal{L}=x\cdot w^2+b^2$，则
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w}=\frac{\partial x\ast {\mathrm{w}}^2}{\partial w}=x\ast 2w\\ \frac{\partial \mathcal{L}}{\partial b}=\frac{\partial b^2}{\partial b}=2b\end{array}$$
考虑目标函数$\mathcal{L}=x\cdot e^w+e^b$，则
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w}=\frac{\partial x\ast {\mathrm{e}}^{\mathrm{w}}}{\partial w}=x\ast {\mathrm{e}}^{\mathrm{w}}\\ \frac{\partial \mathcal{L}}{\partial b}=\frac{\partial e^b}{\partial b}=e^b\end{array}$$
考虑目标函数$\mathcal{L}=[y-(xw+b){]}^2=[(xw+b)-y{]}^2$,令 = + − y
$$\frac{\partial \mathcal{L}}{\partial w}=2\mathrm{g}\ast \frac{\partial \mathrm{g}}{\partial w}=2g\ast x=2(xw+b-y)\ast x$$
$$\frac{\partial \mathcal{L}}{\partial b}=2\mathrm{g}\ast \frac{\partial \mathrm{g}}{\partial b}=2g\ast 1=2(xw+b-y)$$
考虑目标函数ℒ = ( + )，令 = + ，则
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w}=\mathrm{a}\ast \frac{1}{g}\ast \frac{\partial \mathrm{g}}{\partial w}=\frac{a}{xw+b}\ast x\\ \frac{\partial \mathcal{L}}{\partial b}=\mathrm{a}\ast \frac{1}{g}\ast \frac{\partial \mathrm{g}}{\partial b}=\frac{a}{xw+b}\end{array}$$

7.3 激活函数导数

7.3.1 Sigmoid 函数导数

回顾 Sigmoid 函数表达式：
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
我们来推导 Sigmoid 函数的导数表达式：

可以看到，Sigmoid 函数的导数表达式最终可以表达为激活函数的输出值的简单运算，利用这一性质，在神经网络的梯度计算中，通过缓存每层的 Sigmoid 函数输出值，即可在需要的时候计算出其导数。Sigmoid 函数的导数曲线如图 7.2 所示。

为了不使用 TensorFlow 的自动求导功能，本章将使用 Numpy 实现一个通过反向传播算法优化的多层神经网络，因此本章的实现部分我们使用 Numpy 演示，实现 Sigmoid 函数的导数：

# 导入 numpy 库
import numpy as np 
from matplotlib import pyplot as plt
plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = ['STKaiti']
plt.rcParams['axes.unicode_minus'] = False

def set_plt_ax():
    # get current axis 获得坐标轴对象
    ax = plt.gca()                                           

    ax.spines['right'].set_color('none') 
    # 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边
    ax.spines['top'].set_color('none')         

    ax.xaxis.set_ticks_position('bottom')   
    # 指定下边的边作为 x 轴，指定左边的边为 y 轴
    ax.yaxis.set_ticks_position('left') 

    # 指定 data  设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
    ax.spines['bottom'].set_position(('data', 0)) 
    ax.spines['left'].set_position(('data', 0))

def sigmoid(x): 
    # 实现 sigmoid 函数
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x): 
    # sigmoid 导数的计算
    # sigmoid 函数的表达式由手动推导而得
    return sigmoid(x)*(1-sigmoid(x))

x = np.arange(-6.0, 6.0, 0.1)
sigmoid_y = sigmoid(x)
sigmoid_derivative_y = sigmoid_derivative(x)

set_plt_ax()
plt.plot(x, sigmoid_y, color='C9', label='Sigmoid')
plt.plot(x, sigmoid_derivative_y, color='C4', label='导数')
plt.xlim(-6, 6)
plt.ylim(0, 1)
plt.legend(loc=2)
plt.show()

7.3.2 ReLU 函数导数

回顾 ReLU 函数的表达式：
$$\mathrm{ReLU}(x):=\max (0,x)$$
它的导数推导非常简单，直接可得
$$\frac{d}{dx}\mathrm{Re}LU=\{\begin{array}{ll}1& x\ge 0\\ 0& x<0\end{array}$$
可以看到，ReLU 函数的导数计算简单，x 大于等于零的时候，导数值恒为 1，在反向传播的时候，它既不会放大梯度，造成梯度爆炸(Gradient exploding)；也不会缩小梯度，造成梯度弥散(Gradient vanishing)。ReLU 函数的导数曲线如图 7.3 所示。

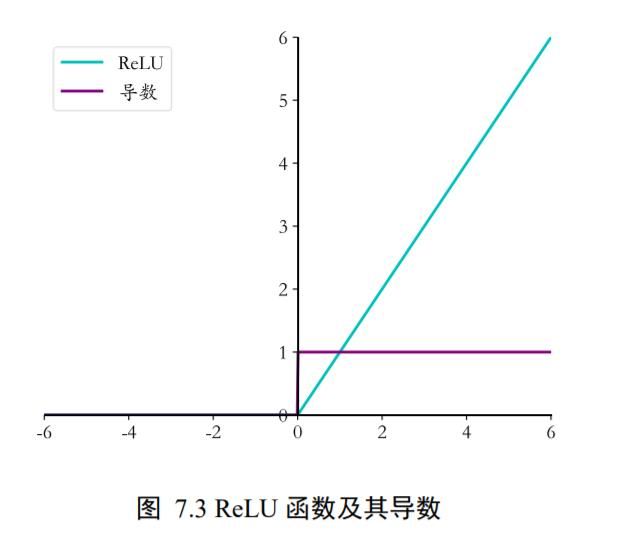
在 ReLU 函数被广泛应用之前，神经网络中激活函数采用 Sigmoid 居多，但是 Sigmoid函数容易出现梯度弥散现象，当网络的层数增加后，较前层的参数由于梯度值非常微小，参数长时间得不到(有效)更新，无法训练深层神经网络，导致神经网络的研究一直停留在浅层；随着 ReLU 函数的提出，很好的解决了梯度弥散的现象，神经网络的层数能够地达到较深层数，如 AlexNet 中采用了 ReLU 激活函数，层数达到了 8 层，后续提出的上百层的卷积神经网络也多是采用 ReLU 激活函数。

通过 Numpy，我们可以方便地实现 ReLU 函数的导数：

def relu(x):
    return np.maximum(0, x)

def relu_derivative(x): # ReLU 函数的导数
    d = np.array(x, copy=True) # 用于保存梯度的张量
    d[x < 0] = 0 # 元素为负的导数为 0
    d[x >= 0] = 1 # 元素为正的导数为 1
    return d

x = np.arange(-6.0, 6.0, 0.1)
relu_y = relu(x)
relu_derivative_y = relu_derivative(x)

set_plt_ax()
plt.plot(x, relu_y, color='C9', label='ReLU')
plt.plot(x, relu_derivative_y, color='C4', label='导数')
plt.xlim(-6, 6)
plt.ylim(0, 6)
plt.legend(loc=2)
plt.show()

7.3.3 LeakyReLU 函数导数

回顾 LeakyReLU 函数的表达式：
$$\text{ LeakyReLU }=\{\begin{array}{cl}x& x\ge 0\\ p\ast x& x\le 0\end{array}$$
它的导数可以推导为
$$\frac{d}{dx}\text{ LeakyReLU }=\{\begin{array}{ll}1& x\ge 0\\ p& x<0\end{array}$$
它和 ReLU 函数的不同之处在于，当 x 小于零时，LeakyReLU 函数的导数值并不为 0，而是，p 一般设置为一个较小的数值，如 0.01 或 0.02，LeakyReLU 函数的导数曲线如图 7.4所示。

LeakyReLU 函数有效的克服了 ReLU 函数的缺陷，使用也比较广泛。我们可以通过Numpy 实现 LeakyReLU 函数的导数如下：

def leakyrelu(x, p):
    y = np.copy(x)
    y[y < 0] = p * y[y < 0]
    return y

# 其中 p 为 LeakyReLU 的负半段斜率，为超参数
def leakyrelu_derivative(x, p):
    dx = np.ones_like(x) # 创建梯度张量，全部初始化为 1
    dx[x < 0] = p # 元素为负的导数为 p
    return dx

x = np.arange(-6.0, 6.0, 0.1)
p = 0.1
leakyrelu_y = leakyrelu(x, p)
leakyrelu_derivative_y = leakyrelu_derivative(x, p)

set_plt_ax()
plt.plot(x, leakyrelu_y, color='C9', label='LeakyReLU')
plt.plot(x, leakyrelu_derivative_y, color='C4', label='导数')
plt.xlim(-6, 6)
plt.yticks(np.arange(-1, 7))
plt.legend(loc=2)
plt.show()

7.3.4 Tanh 函数梯度

回顾 tanh 函数的表达式：
$$\tanh (x)=\frac{\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)}$$

$$=2\ast \mathrm{sigmoid}(2x)-1$$
它的导数推导为
$$\begin{array}{rl}\frac{d}{dx}\tanh (x)& =\frac{\left(e^x+e^{-x}\right)\left(e^x+e^{-x}\right)-\left(e^x-e^{-x}\right)\left(e^x-e^{-x}\right)}{{\left(e^x+e^{-x}\right)}^2}\\ & =1-\frac{{\left(e^x-e^{-x}\right)}^2}{{\left(e^x+e^{-x}\right)}^2}=1-{\tanh }^2(x)\end{array}$$
tanh 函数及其导数曲线如图 7.5 所示。

在 Numpy 中，可以实现 Tanh 函数的导数如下：

def sigmoid(x): # sigmoid 函数实现
    return 1 / (1 + np.exp(-x))
    
def tanh(x): # tanh 函数实现
    return 2*sigmoid(2*x) - 1
    
def tanh_derivative(x): # tanh 导数实现
    return 1-tanh(x)**2

x = np.arange(-6.0, 6.0, 0.1)
tanh_y = tanh(x)
tanh_derivative_y = tanh_derivative(x)

set_plt_ax()
plt.plot(x, tanh_y, color='C9', label='Tanh')
plt.plot(x, tanh_derivative_y, color='C4', label='导数')
plt.xlim(-6, 6)
plt.ylim(-1.5, 1.5)
plt.legend(loc=2)
plt.show()

7.4 损失函数梯度

前面已经介绍了常见的损失函数，我们这里推导均方误差损失函数和交叉熵损失函数的梯度表达式。

7.4.1 均方误差函数梯度

均方差损失函数表达式为：
$$\mathcal{L}=\frac{1}{2}\sum _{k=1}^K{\left(y_k-o_k\right)}^2$$

则它的偏导数$\frac{\partial \mathcal{L}}{\partial o_i}$可以展开为

$$\frac{\partial \mathcal{L}}{\partial o_i}=\frac{1}{2}\sum _{k=1}^K\frac{\partial }{\partial o_i}{\left(y_k-o_k\right)}^2$$

利用链式法则分解为
$$\frac{\partial \mathcal{L}}{\partial o_i}=\frac{1}{2}\sum _{k=1}^{K}2\ast \left(y_k-o_k\right)\ast \frac{\partial \left(y_k-o_k\right)}{\partial o_i}$$
即
$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial o_i}& =\sum _{k=1}^K\left(y_k-o_k\right)\cdot -1\cdot \frac{\partial o_k}{\partial o_i}\\ & =\sum _{k=1}^K\left(o_k-y_k\right)\cdot \frac{\partial o_k}{\partial o_i}\end{array}$$
$\frac{\partial o_k}{\partial o_i}$仅当 = 时才为 1，其他点都为 0，也就是说，$\frac{\partial L}{\partial {\theta }_i}$只与第 $i$号节点相关，与其他节点无关。因此上式中的求和符号可以去掉。均方差的导数可以推导为：
$$\frac{\partial \mathcal{L}}{\partial o_i}=\left(o_i-y_i\right)$$

7.4.2 交叉熵函数梯度

可以参考文章：Softmax函数详解以及求导过程

在计算交叉熵损失函数时，一般将Softmax函数与交叉熵函数统一实现。我们先推导Softmax 函数的梯度，再推导交叉熵函数的梯度。

7.4.2.1Softmax 梯度

回顾 Softmax 函数的表达式：

$$p_i=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}$$

它的功能是将 $K$个输出节点的值转换为概率，并保证概率之和为 1，如图 7.6 所示。

回顾
$$f(x)=\frac{g(x)}{h(x)}$$

函数的导数

$$f^{\prime }(x)=\frac{g^{\prime }(x)h(x)-h^{\prime }(x)g(x)}{h(x{)}^2}$$
对于 Softmax 函数，$g(x)=e^{z_i},h(x)={\sum }_{k=1}^K{e}^{z_k}$,下面我们根据 = 时和 ≠ 来分别推导Softmax 函数的梯度。

❑ 当 = 时 Softmax 函数的偏导数可以展开为

提取公共项$e^{Z_i}$=

拆分为 2 部分=

可以看到，它们即是 2 个概率值的相乘，同时 = j ：= (1 − j )

❑ 当 ≠ 时 展开 Softmax 函数为

$$\frac{\partial \frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}}{\partial z_j}=\frac{0-e^{z_j}{e}^{z_i}}{{\left({\sum }_{k=1}^K{e}^{z_k}\right)}^2}$$
去掉 0 项，并分解为 2 项
$$\begin{array}{c}=\frac{-e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}\times \frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}\\ =-p_j\cdot p_i\end{array}$$
可以看到，虽然 Softmax 函数的梯度推导稍复杂，但是最终的结果还是很简洁的：

7.4.2.2交叉熵梯度

考虑交叉熵损失函数的表达式
$$\mathcal{L}=-\sum _k{y}_k\log \left(p_k\right)$$
我们直接来推导最终损失函数对网络输出 logits 变量$z_i$的偏导数，展开为
$$\frac{\partial \mathcal{L}}{\partial z_i}=-\sum _k{y}_k\frac{\partial \log \left(p_k\right)}{\partial z_i}$$

将 ℎ复合函数利用链式法则分解为
$$=-\sum _k{y}_k\frac{\partial \log \left(p_k\right)}{\partial p_k}\times \frac{\partial p_k}{\partial z_i}$$
即
$$=-\sum _k{y}_k\frac{1}{p_k}\times \frac{\partial p_k}{\partial z_i}$$
其中$\frac{\partial p_k}{\partial z_i}$即为我们已经推导的 Softmax 函数的偏导数。

将求和符号分开为 = 以及 ≠ 的 2 种情况，并代入$\frac{\partial p_k}{\partial z_i}$求解的公式，可得
$$\frac{\partial \mathcal{L}}{\partial z_i}=-y_i\left(1-p_i\right)-\sum _{k\ne i}{y}_k\frac{1}{p_k}\left(-p_k\cdot p_i\right)$$
进一步化简为
$$\begin{array}{rl}& =-y_i\left(1-p_i\right)+\sum _{k\ne i}{y}_k\cdot p_i\\ & =-y_i+y_i{p}_i+\sum _{k\ne i}{y}_k\cdot p_i\end{array}$$
提供公共项$p_i$
$$=p_i\left(y_i+\sum _{k\ne i}{y}_k\right)-y_i$$
完成交叉熵函数的梯度推导。

特别地，对于分类问题中 y 通过 one-hot 编码的方式，则有
$$\begin{array}{rl}& \sum _k{y}_k=1\\ & y_i+\sum _{k\ne i}{y}_k=1\end{array}$$
因此交叉熵的偏导数可以进一步简化为
$$\frac{\partial \mathcal{L}}{\partial {\mathbf{z}}_i}=p_i-y_i$$

7.5 全连接层梯度

在介绍完梯度的基础知识后，我们正式地进入到神经网络的反向传播算法的推导中。实际使用中的神经网络的结构多种多样，我们将以全连接层，激活函数采用 Sigmoid 函数，误差函数为 Softmax+MSE 损失函数的神经网络为例，推导其梯度传播方式。

7.5.1 单个神经元梯度

对于采用 Sigmoid 激活函数的神经元模型，它的数学模型可以写为

$$o^1=\sigma \left(w^{1}x+b^1\right)$$

其中变量的上标表示层数，如$o^1$表示第一个隐藏层的输出，表示网络的输入，我们以权值的偏导数推导为例。

为了方便演示，我们将神经元模型绘制如图 7.7 所示，图中未画出偏置，输入节点数为J。其中输入第个节点到输出$o^1$的权值连接记为$w_{j1}^1$，上标表示权值属于的层数，下标表示当前连接的起始节点号和终止节点号，如下标1表示上一层的第号节点到当前层的 1 号节点。经过激活函数之前的变量叫做$z_1^1$，经过激活函数之后的变量叫$o^1$，由于只有一个输出节点，$o_1^1$ = $o^1$。输出与真实标签之间计算误差，误差记为ℒ。

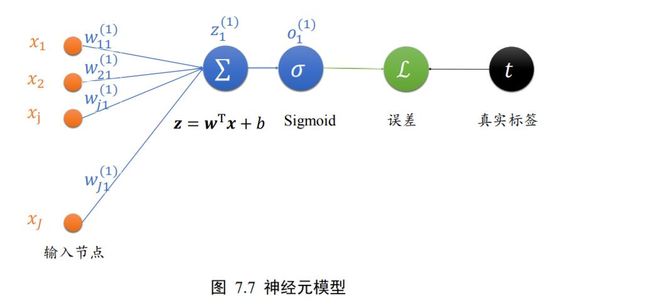
如果我们采用均方差误函数，考虑到单个神经元只有一个输出$o_1^1$，那么损失可以表
达为
$$\mathcal{L}=\frac{1}{2}{\left(o_1^1-t\right)}^2$$
其中为真实标签值，添加1/2并不影响梯度的方向，计算更简便。我们以权值连接的第 ∈[1,]号节点的权值$w_{j1}$为例，考虑损失函数ℒ对其的偏导数 $\frac{\partial \mathcal{L}}{\partial w_{j1}}$:
$$\frac{\partial \mathcal{L}}{\partial w_{j1}}=\left(o_1-t\right)\frac{\partial o_1}{\partial w_{j1}}$$
将$o_1=\sigma \left(z_1\right)$分解，考虑到 Sigmoid 函数的导数${\sigma }^{\prime }=\sigma (1-\sigma )$：
$$\begin{array}{rl}& \frac{\partial \mathcal{L}}{\partial w_{j1}}=\left(o_1-t\right)\frac{\partial \sigma \left(z_1\right)}{\partial w_{j1}}\\ =& \left(o_1-t\right)\sigma \left(z_1\right)\left(1-\sigma \left(z_1\right)\right)\frac{\partial z_1^1}{\partial w_{j1}}\end{array}$$
$\sigma \left(z_1\right)$写成$o_1$，继续推导 $\frac{\partial \mathcal{L}}{\partial w_{j1}}$:

$$\frac{\partial \mathcal{L}}{\partial w_{j1}}=\left(o_1-t\right)o_1\left(1-o_1\right)\frac{\partial z_1^1}{\partial w_{j1}}$$
考虑 $\frac{\partial z_1^1}{\partial w_{j1}}=x_j$，可得：
$$\frac{\partial \mathcal{L}}{\partial w_{j1}}=\left(o_1-t\right)o_1\left(1-o_1\right)x_j$$
从上式可以看到，误差对权值$w_{j1}$的偏导数只与输出值$o_1$、真实值以及当前权值连接的输入$x_j$有关。

7.5.2 全连接层梯度

我们把单个神经元模型推广到单层全连接层的网络上，如图 7.8 所示。输入层通过一个全连接层得到输出向量1，与真实标签向量计算均方误差。输入节点数为 $J$，输出节点数为 $K$。

多输出的全连接网络层模型与单个神经元模型不同之处在于，它多了很多的输出节点$o_1^1,o_2^1,o_3^1,\dots ,o_K^1$，同样的每个输出节点分别对应到真实标签$t_1,t_2,\dots ,t_K$。均方误差可以表达为
$$\mathcal{L}=\frac{1}{2}\sum _{i=1}^K{\left(o_i^1-t_i\right)}^2$$
由于 $\frac{\partial \mathcal{L}}{\partial w_{jk}}$只与节点$o_k^1$有关联，上式中的求和符号可以去掉，即 = ：
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_k-t_k\right)\frac{\partial o_k}{\partial w_{jk}}$$
将$o_k=\sigma \left(z_k\right)$代入
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_k-t_k\right)\frac{\partial \sigma \left(z_k\right)}{\partial w_{jk}}$$
考虑 Sigmoid 函数的导数′ = (1 − )：
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_k-t_k\right)\sigma \left(z_k\right)\left(1-\sigma \left(z_k\right)\right)\frac{\partial z_k^1}{\partial w_{jk}}$$
将$\sigma \left(Z_k\right)$记为$O_k$：
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_k-t_k\right)o_k\left(1-o_k\right)\frac{\partial z_k^1}{\partial w_{jk}}$$
最终可得
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_{\mathrm{k}}-t_k\right)o_k\left(1-o_k\right)x_j$$
由此可以看到，某条连接$W_{jk}$上面的连接，只与当前连接的输出节点$O_k^1$，对应的真实值节点的标签$t_k^1$，以及对应的输入节点$X_j$有关。
我们令${\delta }_k=\left(o_k-t_k\right)o_k\left(1-o_k\right)$,则$\frac{\partial \mathcal{L}}{\partial w_{jk}}$可以表达为
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}={\delta }_k{x}_j$$
其中${\delta }_k$变量表征连接线的终止节点的梯度传播的某种特性，使用${\delta }_k$表示后，$\frac{\partial \mathcal{L}}{\partial w_{jk}}$偏导数只与当前连接的起始节点$x_j$，终止节点处${\delta }_k$有关，理解起来比较直观。后续我们将会在看到${\delta }_k$在循环推导梯度中的作用。

现在我们已经推导完单层神经网络(即输出层)的梯度传播方式，接下来我们尝试推导倒数第二层的梯度传播公式，完成了导数第二层的传播推导，可以循环往复推导所有隐藏层的梯度传播公式，从而完成所有参数的梯度计算。

在介绍反向传播算法之前，我们先学习一个导数传播的核心法则：链式法则。

7.6 链式法则

前面我们介绍了输出层的梯度 $\frac{\partial \mathcal{L}}{\partial w_{jk}}$计算方法，我们现在来介绍链式法则，它是能在不显式推导神经网络的数学表达式的情况下，逐层推导梯度的核心公式，非常重要。
其实我们前面在推导梯度的过程中已经或多或少地用到了链式法则。考虑复合函数$y=f(u),u=g(x)$，则$\frac{dy}{dx}$可由$\frac{dy}{du}$和$\frac{du}{dx}$推导出：
$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}=f^{\prime }(g(x))\cdot g^{\prime }(x)$$
考虑多元复合函数， = (, )，其中 = (), = ℎ()，那么$\frac{dz}{dt}$的导数可以由$\frac{dz}{dx}$和$\frac{dz}{dy}$等推导出，具体表达为
$$\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}$$
例如，$z=(2t+1{)}^2+e^{t^2}$，令 = 2 + 1, $y=t^2$,则$z=x^2+e^y$
$$\begin{array}{r}\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}=2x\ast 2+e^y\ast 2t\\ \frac{dz}{dt}=2(2t+1)\ast 2+e^{t^2}\ast 2t\\ \frac{dz}{dt}=4(2t+1)+2t{e}^{t^2}\end{array}$$
神经网络的损失函数ℒ来自于各个输出节点$O_k^K$，如下图 7.9 所示，其中输出节点$O_k^K$又与隐藏层的输出节点$O_j^J$相关联，因此链式法则非常适合于神经网络的梯度推导。让我们来考虑损失函数ℒ如何应用链式法则。

前向传播时，数据经过$w_{ij}^J$传到倒数第二层的节点$O_j^J$，再传播到输出层的节点$O_k^K$。在每层只有一个节点时， $\frac{\partial \mathcal{L}}{\partial w_{jk}^1}$可以利用链式法则，逐层分解为：
$$\frac{\partial \mathcal{L}}{\partial w_{ij}^J}=\frac{\partial \mathcal{L}}{\partial o_j^J}\frac{\partial o_j^J}{\partial w_{ij}^J}=\frac{\partial \mathcal{L}}{\partial o_k^K}\frac{\partial o_k^K}{\partial o_j^J}\frac{\partial o_j^J}{\partial w_{ij}^J}$$
其中 $\frac{\partial \mathcal{L}}{\partial o_k^K}$可以由误差函数直接推导出，$\frac{\partial o_k^K}{\partial o_j^J}$可以由全连接层公式推导出，$\frac{\partial o_j^J}{\partial w_{ij}^J}$的导数即为输入$x_i^I$。可以看到，通过链式法则，我们不需要显式计算$\mathcal{L}=f\left(w_{ij}^J\right)$的具体数学表达式，直接可以将偏导数分解，层层迭代即可推导出。

我们简单使用 TensorFlow 来体验链式法则的魅力：

import tensorflow as tf
#构建待优化变量
x=tf.constant(1.)
w1=tf.constant(2.)
b1=tf.constant(1.)
w2=tf.constant(2.)
b2=tf.constant(1.)
# 构建梯度记录器
with tf.GradientTape(persistent=True) as tape:
    # 非tf.Variable类型的张量需要人为设置记录梯度信息
    tape.watch([w1,b1,w2,b2])
    #构建两层线性网络
    y1=x*w1+b1
    y2=y1*w2+b2

# 独立求解出各个偏导数
dy2_dy1=tape.gradient(y2,[y1])[0]
dy1_dw1=tape.gradient(y1,[w1])[0]
dy2_dw1=tape.gradient(y2,[w1])[0]

#验证连式法则
print(dy2_dy1*dy1_dw1)
print(dy2_dw1)

我们通过自动求导功能计算出$\frac{\partial y_2}{\partial y_1}$，$\frac{\partial y_1}{\partial w_1}$和$\frac{\partial y_2}{\partial w_1}$，借助链式法则我们可以推断$\frac{\partial y_2}{\partial y_1}$*$\frac{\partial y_1}{\partial w_1}$与$\frac{\partial y_2}{\partial w_1}$应该是相等的，他们的计算结果如下：

tf.Tensor(2.0, shape=(), dtype=float32)
tf.Tensor(2.0, shape=(), dtype=float32)

可以看到$\frac{\partial y_2}{\partial y_1}\ast \frac{\partial y_1}{\partial w_1}=\frac{\partial y_2}{\partial w_1}$，偏导数的传播是符合链式法则的。

7.7 反向传播算法

现在我们来推导隐藏层的反向传播算法。简单回顾一下输出层的偏导数公式：
$$\frac{\partial \mathcal{L}}{\partial w_{jk}}=\left(o_k-t_k\right)o_k\left(1-o_k\right)x_j={\delta }_k{x}_j$$
考虑网络倒数第二层的偏导数 $\frac{\partial \mathcal{L}}{\partial w_{ij}}$，如图 7.10 所示，输出层节点数为 K，输出为$O^k=$$\left[o_1^K,o_2^K,\dots ,o_K^K\right]$；倒数第二层节点数为 $J$，输出为$O^j=$$\left[o_1^j,o_2^j,\dots ,o_j^j\right]$；倒数第三层的节点数为 $I$，输出为$O^i=$$\left[o_1^i,o_2^i,\dots ,o_i^i\right]$.

首先将均方差误差函数展开：
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\frac{\partial }{\partial w_{ij}}\frac{1}{2}\sum _k{\left(o_k-t_k\right)}^2$$

由于ℒ通过每个输出节点$o_k$与$w_{ij}$ 相关联，故此处不能去掉求和符号，运用链式法则将均方
差函数拆解：

$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\sum _k\left(o_k-t_k\right)\frac{\partial }{\partial w_{ij}}{o}_k$$

将$o_k=\sigma \left(z_k\right)$代入

$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\sum _k\left(o_k-t_k\right)\frac{\partial }{\partial w_{ij}}\sigma \left(z_k\right)$$

利用 Sigmoid 函数的导数′ = (1 − )进一步分解
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\sum _k\left(o_k-t_k\right)\frac{\partial }{\partial w_{ij}}\sigma \left(z_k\right)$$

将$\sigma \left(z_k\right)$写回$o_k$形式，并利用链式法则，将$\frac{\partial z_k}{\partial w_{ij}}$分解
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\sum _k\left(o_k-t_k\right)o_k\left(1-o_k\right)\frac{\partial z_k}{\partial o_j}\cdot \frac{\partial o_j}{\partial w_{ij}}$$

其中$\frac{\partial z_k}{\partial o_j}=w_{jk}$，因此
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\sum _k\left(o_k-t_k\right)o_k\left(1-o_k\right)w_{jk}\frac{\partial o_j}{\partial w_{ij}}$$

考虑到 $\frac{\partial o_j}{\partial w_{ij}}$与 k 无关，可提取公共项
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=\frac{\partial o_j}{\partial w_{ij}}\sum _k\left(o_k-t_k\right)o_k\left(1-o_k\right)w_{jk}$$

进一步利用$o_j=\sigma \left(z_j\right)$，并利用 Sigmoid 导数${\sigma }^{\prime }=\sigma (1-\sigma )$将$\frac{\partial o_j}{\partial w_{ij}}$拆分为
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=o_j\left(1-o_j\right)\frac{\partial z_j}{\partial w_{ij}}\sum _k\left(o_k-t_k\right)o_k\left(1-o_k\right)w_{jk}$$

其中$\frac{\partial z_j}{\partial w_{ij}}$的导数可直接推导出为$O_i$，上式可写为
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=o_j\left(1-o_j\right)o_i\sum _k\underset{{\delta }_k^K}{\left(o_k-t_k\right)o_k\left(1-o_k\right)}{w}_{jk}$$
其中${\delta }_k^K=\left(o_k-t_k\right)o_k\left(1-o_k\right)$，则 $\frac{\partial \mathcal{L}}{\partial w_{ij}}$的表达式可简写为
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}=o_j\left(1-o_j\right)o_i\sum _{\mathbf{k}}{\delta }_k^K{w}_{jk}$$
我们仿照输出层$\frac{\partial \mathcal{L}}{\partial w_{jk}}={\delta }_k^K{x}_j$的书写方式，将${\delta }_j^J$定义为
$${\delta }_j^J:=o_j\left(1-o_j\right)\sum _k{\delta }_k^K{w}_{jk}$$

此时$\frac{\partial \mathcal{L}}{\partial w_{ij}}$可以写为当前连接的起始节点的输出值$o_i$与终止节点 j 的梯度信息${\delta }_j^J$的简单相乘运算：
$$\frac{\partial \mathcal{L}}{\partial w_{ij}}={\delta }_j^J{O}_i^I$$
通过定义变量，每一层的梯度表达式变得更加清晰简洁，其中可以简单理解为当前连接$w_{ij}$对误差函数的贡献值。

我们来小结一下每层的偏导数的计算公式。

输出层：
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w_{jk}}={\delta }_k^K{o}_j\\ {\delta }_k^K=o_k\left(1-o_k\right)\left(o_k-t_k\right)\end{array}$$

倒数第二层：
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w_{ij}}={\delta }_j^J{o}_i\\ {\delta }_j^J=o_j\left(1-o_j\right){\sum }_k{\delta }_k^K{w}_{jk}\end{array}$$
倒数第三层：
$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial w_{ni}}={\delta }_i^I{o}_n\\ {\delta }_i^I=o_i\left(1-o_i\right){\sum }_j{\delta }_j^J{w}_{ij}\end{array}$$

其中$O_n$为倒数第三层的输入，即倒数第四层的输出。

依照此规律，只需要循环迭代计算每一层每个节点的${\delta }_k^K,{\delta }_j^J,{\delta }_i^I,\dots$等值即可求得当前层的偏导数，从而得到每层权值矩阵$W$的梯度，再通过梯度下降算法迭代优化网络参数即可。

至此，反向传播算法介绍完毕。

接下来我们会进行两个实战：第一个实战是采用 TensorFlow 提供的自动求导来优化Himmelblau 函数的极小值；第二个实战是基于 Numpy 实现反向传播算法，并完成多层