word2vec 模型的详细数学推导和直观理解

word2vec作为一个优秀的用于产生词向量开源工具，在自然语言处理和计算机视觉领域有着很多应用，实践中效果相当好，但是很多使用者往往知其然不知其所以然。本文对word2vec Parameter Learning Explained这篇文章进行翻译和解读。深入浅出地剖析了词嵌入模型的参数学习过程，给出了详细的数学推导以及直观的解释。看完对word2vec会有一个更深层次的理解，有利于更好地使用和改进这一工具。

说明：读本文之前，需要对神经网络及后向传播有一定了解。另外，对word2vec需要有一个大概的了解。

1 连续词袋模型（CBOW）

1.1 单个单词上下文

从一个最简单的连续词袋模型开始，假设上下文只有一个单词，即输入一个目标单词，预测一个单词（而不是多个）。
下图是在上述定义之下的网络模型。

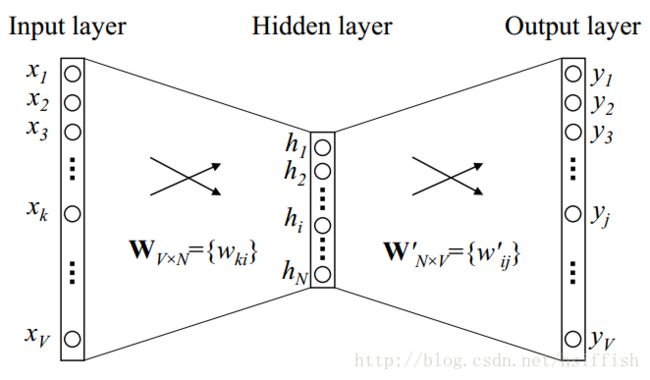
上图中，词汇量大小为 V V ，隐藏层大小为 N N ，各层直接都是全连接。输入是一个one-hot向量，即对于一个给定的上下文单词， V V 个元素 {x1,...xV} { x 1 , . . . x V } 中只有一个为1，其他均为0。

解释：每个输入的向量 {x1,...xV} { x 1 , . . . x V } 有 V V 个元素，一个元素 xk x k 代表一个单词。如果向量表示第 k k 个单词， xk x k 为1，其他元素均为0。

为了让大家有一个更直观具体的理解，这里给出一个具体的例子，图中假设 V=6 V = 6 ， N=3 N = 3 。

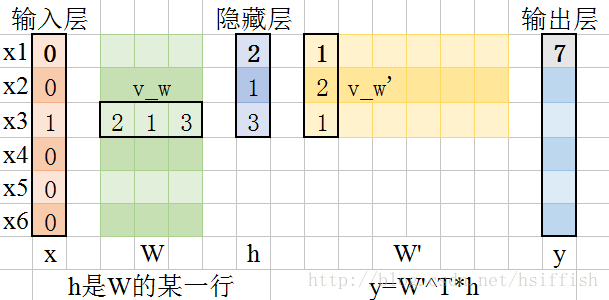
输入层和隐藏层之间的权重可以用一个 V×N V × N 矩阵 W W 表示， W W 的每一行是一个 N N 维的向量 vw v w ，表示输入层对应的单词， W W 的第 i i 行用 vTw v w T 表示，给定一个上下文（在这个模型中即为一个单词），假设 xk=1,xk′=0,k′≠k x k = 1 , x k ′ = 0 , k ′ ≠ k ，有以下式子：

h=WTx=WTk,.:=vwI(1) h = W T x = W k , . T := v w I ( 1 )

上式本质上是将 W W 的第 k k 行复制给 h h 。 vwI v w I 是输入单词 wI w I 的向量表示。这表示隐藏层的激活函数是一个简单的线性函数（比如，直接将输入的加权和传递到下一层）。
隐藏层和输出层之间，有一个不同的权重矩阵 W′={w′ij} W ′ = { w i j ′ } ，这是一个 N×V N × V 矩阵。使用这些权重，我们可以计算词汇表（ V V 个单词组成的词汇表）中每一个单词的分值 uj u j ：

uj=v′Twjh(2) u j = v w j ′ T h ( 2 )

其中， v′wj v w j ′ 是矩阵 W′ W ′ 的第 j j 列。

解释：输出共有 V V 个元素，每一个元素由 W W 的第 j j 列和 h h 相乘得到（加权和），即为 uj u j 。

接着我们使用softmax，一个log线性分类器模型，以得到每个单词的后验概率，这是一个多项式分布：

p(wj|wI)=yj=exp(uj)∑Vj′=1exp(uj′)(3) p ( w j | w I ) = y j = e x p ( u j ) ∑ j ′ = 1 V e x p ( u j ′ ) ( 3 )

其中， yj y j 是输出层的第 j j 个元素。
将（1）式和（2）式代入（3）式有：

p(wj|wI)=yj=exp(v′TwjvwI)∑Vj′=1exp(v′TwjvwI)(4) p ( w j | w I ) = y j = e x p ( v w j ′ T v w I ) ∑ j ′ = 1 V e x p ( v w j ′ T v w I ) ( 4 )

注意 vw v w 和 v′w v w ′ 是词语 w w 的两个表示。 vw v w 来自输入层和隐藏层间的权重矩阵 W W 的行， vw‘′ v w ‘ ′ 来自隐藏层和输出层间的权重矩阵 W′ W ′ 的列。在接下来的分析中，我们称 vw v w 为词语 w w 的输入向量，称 v′w v w ′ 为词语 w w 的输出向量。

注意：在一次训练中，输入向量和输出向量不是同一个向量，不是代表同一个词语，输入的是上下文词语，输出的是由上下文推导而来的词语。

隐藏层到输出层的权重更新等式

先说更新思路，目标是最大化 p(wO|wI) p ( w O | w I ) ，即要最小化损失函数 E E 。因此找到权重关于 E E 的公式，求偏导得到梯度，利用梯度更新权重，使得 E E 尽快下降。

尽管实际进行这种权重更新计算是不切实际的（下文有解释），但我们探究这个源头有利于理解没用任何技巧的初始模型。
我们训练的目标是为了最大化式（4）：

maxp(wO|wI)=maxyj∗(5)=maxlogyj∗(6)=uj∗−log∑j′=1Vexp(uj′):=−E(7) max p ( w O | w I ) = max y j ∗ ( 5 ) = max log ⁡ y j ∗ ( 6 ) = u j ∗ − log ⁡ ∑ j ′ = 1 V exp ⁡ ( u j ′ ) := − E ( 7 )

解释：式子（7）由对式（6）代入式（2）得到

此处， E=−log(wO|wI) E = − log ⁡ ( w O | w I ) 是我们的损失函数（我们要最小化 E E ）, j∗ j ∗ 是输出层实际输出的单词的指标。注意这个损失函数可以理解为两个概率分布间的交叉熵度量的特例。
现在来推导隐藏层和输出层间的权重。对 E E 进行求关于第 j j 个输出元素 uj u j 的导数，可得：

∂E∂uj=yj−tj:=ej(8) ∂ E ∂ u j = y j − t j := e j ( 8 )

解释：对（7）式求导可得

其中， tj=1(j=j∗) t j = 1 ( j = j ∗ ) ，仅当第 j j 个元素是实际输出单词时， tj=1 t j = 1 ，其他情况 tj=0 t j = 0 ，注意现在这个梯度是输出层的预测错误。
接着对 E E 进行求关于 w′ij w i j ′ 的偏导，以得到隐藏层到输出层权重的梯度：

∂E∂w′ij=∂E∂uj.∂uj∂w′ij=ej.hi(9) ∂ E ∂ w i j ′ = ∂ E ∂ u j . ∂ u j ∂ w i j ′ = e j . h i ( 9 )

解释： ∂uj∂w′ij ∂ u j ∂ w i j ′ 根据公式（2）求导

使用随机梯度下降法，更新权重：

w′(new)ij=w′(old)ij−η.ej.hi(10) w i j ′ ( n e w ) = w i j ′ ( o l d ) − η . e j . h i ( 10 )

或者

v′(new)wj=v′(old)wj−η.ej.hj=1,2,...V(11) v w j ′ ( n e w ) = v w j ′ ( o l d ) − η . e j . h j = 1 , 2 , . . . V ( 11 )

解释：（10）式和（11）式的区别在于， w′ij w i j ′ 是 W′ W ′ 的单个元素， v′wj v w j ′ 是 W′ W ′ 的一列元素。（10）式是单个单个元素更新，（11）式是一列一列更新。

其中， η>0 η > 0 是学习率， ej=yj−tj e j = y j − t j ， hi h i 是隐藏层的第 i i 个元素， v′wj v w j ′ 是 wj w j 输出向量。注意这个更新等式需要将词汇表中的每一个可能单词都过一遍，检查输出概率 yj y j 和期望的输出 tj t j （0或者1）。如果 yj>tj y j > t j （高估），则我们要从 v′wj v w j ′ 减少一定比例的隐藏层向量 h h (比如 vwI v w I )，这使得 v′wj v w j ′ 远离 vwI v w I 。当 yj<tj y j < t j （低估，这种情况仅当 tj=1 t j = 1 时出现，例如， wj=wO w j = w O ），则我们要从增加一定比例的隐藏层向量 h h 到 v′wO v w O ′ ，这使得 v′wO v w O ′ 靠近 vwI v w I 。如果 yj y j 非常靠近 tj t j ，根据更新等式，权重只有非常小的变动。这里要再次强调一下， vw v w （输入向量）和 v′w v w ′ （输出向量）是单词 w w 的两个不同向量表示。

说明：这里说的远近，是使用内积作为衡量标准，而不是欧式距离。
另外， v′wO v w O ′ 和 vwI v w I 代表的不是同一个单词，是目标单词及其上下文，经过模型的训练，单词及其上下文的向量相似性会提高。

为了更好理解权重更新过程，同样可以看这张图，图中假设 V=6 V = 6 ， N=3 N = 3 。

输出层到隐藏层的权重更新等式

得到 W′ W ′ 的更新等式后，同理可以推导得到 W W 的更新等式。对 E E 在输出层到隐藏层之间求导得到：

∂E∂hi=∑j=1V∂E∂uj.∂uj∂hi=∑j=1Vej.w′ij:=EHi(12) ∂ E ∂ h i = ∑ j = 1 V ∂ E ∂ u j . ∂ u j ∂ h i = ∑ j = 1 V e j . w i j ′ := E H i ( 12 )

解释：（12）式由（2）式和（8）式求导可以得到。

此处， hi h i 是隐藏层输出的第 i i 个元素， uj u j 在式（2）中定义，是输出层网络输出的第 j j 个元素， ej=yj−tj e j = y j − t j 是输出层第 j j 个单词的预测误差。 EH E H 是一个 N N 维向量，是单词表所有单词的的输出向量和其预测误差的加和。
接着要对 E E 关于 W W 求导。首先，前文说过，输入层到隐藏层间是线性关系，扩展式（1）可以得到：

hi=∑k=1Vxk.wki(13) h i = ∑ k = 1 V x k . w k i ( 13 )

由上式这个关系以及式（13）就可以得到 E E 关于 W W 的导数：

∂E∂wij=∂E∂hi.∂hi∂w′ki=EHi.xk(14) ∂ E ∂ w i j = ∂ E ∂ h i . ∂ h i ∂ w k i ′ = E H i . x k ( 14 )

上式可以表示为 x x 和 EH E H 的张量：

∂E∂W=x⊗EH=xEHT(15) ∂ E ∂ W = x ⊗ E H = x E H T ( 15 )

经过上式可以得到一个 V×N V × N 矩阵。由于 x x 只有一个元素是非零的，所以 ∂E∂W ∂ E ∂ W 只有一行为非零（这点由张量的定义可以轻易得到），这一行就是 EHT E H T ，一个 N N 维向量。由此可以得到以下的更新等式：

v(new)wI=v(old)wI−ηEHT(16) v w I ( n e w ) = v w I ( o l d ) − η E H T ( 16 )

其中， vwI v w I 是 W W 的一行，是唯一一个上下文的输入向量，也是唯一一个梯度非零的行。 W W 的其他行都保持不变，因为梯度为零。
直观来说，由于向量 EH E H 是词汇表中所有单词的加权输出向量的和（权重为预测误差 ej=yj−tj e j = y j − t j ），我们可以理解式（16）为将词汇表中的每一个输出向量的一部分增加到上下文词语的输入向量。如果，在输出层，单词 wj w j 的成为输出单词的概率被高估（ yj>tj y j > t j ）那么上下文词语 wI w I 的输入向量则要远离输出向量 wj w j ；反之，则要接近。如果 wj w j 的概率非常接近所要的，则对 wI w I 的改动特别小。输入向量 wI w I 的变动由词汇表中所有单词的向量的预测误差决定，预测误差越大，单词对上下文单词的输入向量的影响越大。
通过遍历整个词料库中上下文-目标单词对进行模型参数的迭代更新，每个向量的影响被累加。想象一下，单词 w w 的输出向量被它的共生近邻的上下文的输入向量前前后后“拉扯”着，就像词 w w 的向量和它多个近邻的向量间有着物理绳索一样。类似的，一个输入向量也可以看做被它的多个输出向量“拉扯”着。这个解释与重力，或者力引导分布图类似。每个想象绳索平衡时的长度跟相关词语对的共生强度以及学习率有关。经过多次迭代，输入和输出向量的相关位置最终变得稳定。

1.2 多词语上下文

下图是有多个上下文单词的CBOW模型的图示。

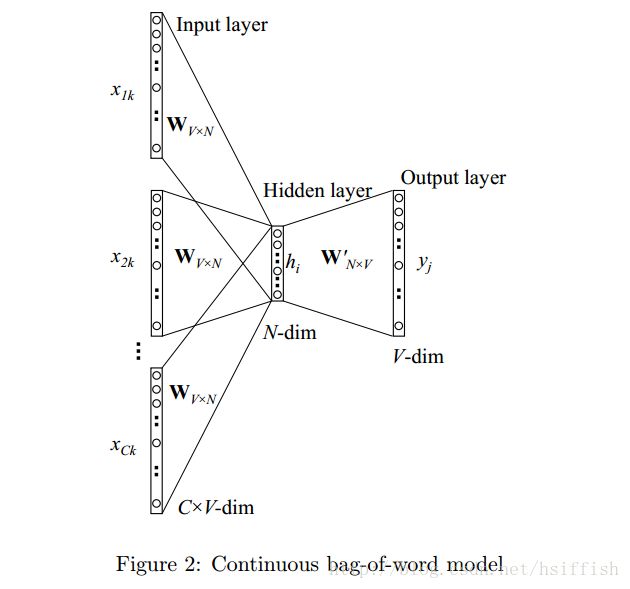
计算隐藏层输出的时，不再像单词语上下文那样，直接复制上下文单词的输入向量，而是取所有上下文单词输入向量的平均值，然后将输入-隐藏层权重矩阵和这个平均值的乘积作为输出：

h=1CWT(x1+x2+...+xC)(17)=1C(vw1+vw2+...+vwC)T(18) h = 1 C W T ( x 1 + x 2 + . . . + x C ) ( 17 ) = 1 C ( v w 1 + v w 2 + . . . + v w C ) T ( 18 )

其中， C C 是输入上下文单词的总数， w1,w2,...,wC w 1 , w 2 , . . . , w C 是上下文单词， vw v w 是单词 w w 的输入向量，损失函数如下：

E=−logp(wO|wI,1,...,wI,C)(19)=−uj∗+log∑j′=1Vexp(uj′)(20)=−v′TwO.h+log∑j′=1Vexp(v′Twj.h)(21) E = − log ⁡ p ( w O | w I , 1 , . . . , w I , C ) ( 19 ) = − u j ∗ + log ⁡ ∑ j ′ = 1 V exp ⁡ ( u j ′ ) ( 20 ) = − v w O ′ T . h + log ⁡ ∑ j ′ = 1 V exp ⁡ ( v w j ′ T . h ) ( 21 )

这个表达式与优化单词语上下文模型的式（7）类似，除了 h h 不同， h h 如式（18）定义，不再是式（1）那个定义。
隐藏层到输出层的权重更新等式和单词语上下文模型的更新等式一样，复制过来如下：

v′(new)wj=v′(old)wj−η.ej.hj=1,2,...V(22) v w j ′ ( n e w ) = v w j ′ ( o l d ) − η . e j . h j = 1 , 2 , . . . V ( 22 )

，注意，对于每一个训练样本，我们要将这个等式应用到隐藏层-输出层间权重矩阵的每一个元素。
输入层到隐藏层间的权重更新等式跟式（16）类似，只是现在需要将下面这个等式应用到每一个输入的上下文单词 wI,c w I , c ：

v(new)wI,c=v(old)wI,c−1CηEHTc=1,2,...C(23) v w I , c ( n e w ) = v w I , c ( o l d ) − 1 C η E H T c = 1 , 2 , . . . C ( 23 )

这里， vwI,c v w I , c 是输入上下文的第 c c 个单词的输入向量， η η 是学习率， ∂E∂hi ∂ E ∂ h i 由式（12）得到。更新等式的直观理解和式（16）一样。

2 Skip-Gram 模型

skip-gram模型由Mikolov等人提出。下图给出了skip-gram模型的图示。

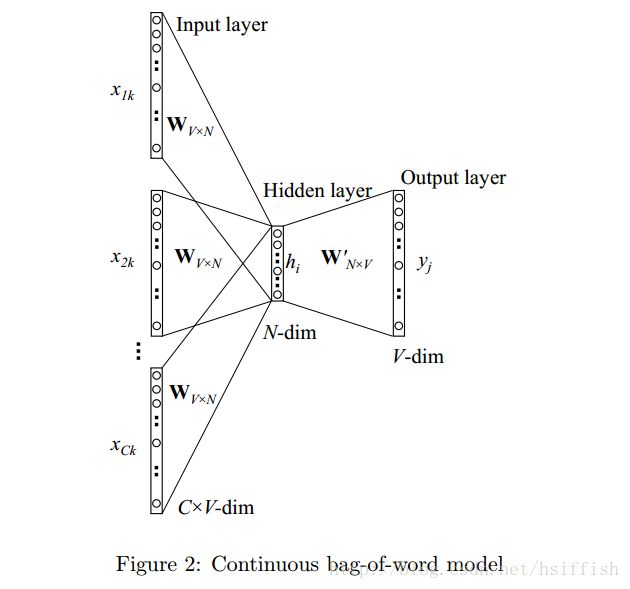
skip-gram模型正好与CBOW模型相反。目标单词现在在输入层，上下文单词在输出层。
我们依然用 vwI v w I 表示输入层的唯一一个单词的输入向量。因此我们可以像（1）一样定义隐藏层输出 h h ：

h=WTx=WTk,.:=vwI(24) h = W T x = W k , . T := v w I ( 24 )

这说明 h h 只是简单地复制输入-隐藏层的权重矩阵 W W 的一行（与输入单词 wI w I 相关的一行）。
在输出层，不再是一个多项式分布，而是输出 C C 个多项式分布。每一个输出用同一个隐藏层-输出层权重矩阵计算：

p(wc,j=wO,c|wI)=yc,j=exp(uc,j)∑Vj′=1exp(u′j)(25) p ( w c , j = w O , c | w I ) = y c , j = e x p ( u c , j ) ∑ j ′ = 1 V e x p ( u j ′ ) ( 25 )

其中， wc,j w c , j 是输出层第 c c 个panel的第 j j 个单词； wO,c w O , c 是实际输出上下文单词中的第 c c 个； wI w I 是唯一的输入单词； yc,j y c , j 是输出层第 c c 版的第 j j 个输出， uj u j 是输出层第 c c 个panel的第 j j 个单元的网络输入。由于输出层的所有panel共享权重，因此有：

uc,j=uj=v′Twjhc=1,2,...,C(26) u c , j = u j = v w j ′ T h c = 1 , 2 , . . . , C ( 26 )

其中， v′wj v w j ′ 是词汇表的第 j j 个单词 wj w j 的输出向量， v′wj v w j ′ 同时也是隐藏层-输出层权重矩阵 W′ W ′ 的一列。
参数更新等式的推导和单一单词上下文的CBOW模型类似。损失函数变为：

E=−logp(wO,1,wO,2,...,wO,C|wI)(27)=−log∏c=1Cexp(uc,j∗c)∑Vj′=1exp(uj′)(28)=−∑c=1Cuj∗c+Clog∑j′=1Vexp(uj′)(29) E = − log ⁡ p ( w O , 1 , w O , 2 , . . . , w O , C | w I ) ( 27 ) = − log ⁡ ∏ c = 1 C exp ⁡ ( u c , j c ∗ ) ∑ j ′ = 1 V exp ⁡ ( u j ′ ) ( 28 ) = − ∑ c = 1 C u j c ∗ + C log ⁡ ∑ j ′ = 1 V exp ⁡ ( u j ′ ) ( 29 )

其中， uj∗c u j c ∗ 是期望输出的第 c c 个上下文单词在词汇表中的下标。
对 E E 关于输出层每一个panel中的每一个单元的网络输出 uc,j u c , j 求偏导：

∂E∂uc,j=yc,j−tc,j:=ec,j(30) ∂ E ∂ u c , j = y c , j − t c , j := e c , j ( 30 )

上式得到单元的预测误差，与（8）中一样。为了方便说明，我们定义一个 V V 维向量 EI={EI1,...,EIV} E I = { E I 1 , . . . , E I V } 作为所有上下文单词的预测误差之和：

EIj=∑c=1Cec,j(31) E I j = ∑ c = 1 C e c , j ( 31 )

接着，对 E E 关于隐藏层到输出层的权重矩阵 W′ W ′ 求偏导：

∂E∂w′ij=∑c=1C∂E∂uc,j.∂uc,j∂w′ij=EIj.hi(32) ∂ E ∂ w i j ′ = ∑ c = 1 C ∂ E ∂ u c , j . ∂ u c , j ∂ w i j ′ = E I j . h i ( 32 )

由上式我们可以得到隐藏层到输出层的权重矩阵 W′ W ′ 的更新等式：

w′(new)ij=w′(old)ij−η.EIj.hi(33) w i j ′ ( n e w ) = w i j ′ ( o l d ) − η . E I j . h i ( 33 )

或者

v′(new)wj=v′(old)wj−η.EIj.hj=1,2,...V(34) v w j ′ ( n e w ) = v w j ′ ( o l d ) − η . E I j . h j = 1 , 2 , . . . V ( 34 )

更新等式的直观理解与式（11）一样，除了预测误差是输出层所有上下文单词的误差的加和。注意，对于每一个样本，我们要应用这个更新等式到隐藏-输出层权重矩阵的每一个元素。
输出-隐藏层的更新等式推导和（12）到（16）一样，除了 ej e j 变为 EIj E I j 。这里直接给出更新等式：

v(new)wI=v(old)wI−ηEHT(35) v w I ( n e w ) = v w I ( o l d ) − η E H T ( 35 )

其中， EH E H 是一个 N N 维向量，每个元素定义为：

EHi=∑j=1VEIj.w′i,j(36) E H i = ∑ j = 1 V E I j . w i , j ′ ( 36 )

（35）的直观理解和（16）一样。

关于模型优化

目前我们讨论的模型（bigram模型，CBOW和skip-gram）都是它们的原始模式，没有应用任何优化技巧。
对于这些模型来说，词汇表中的每一个单词有两个向量表示：输入向量 vw v w 和输出向量 v′w v w ′ 。学习输入向量很轻易，但是学习输出向量花费巨大。从更新等式（22）可以看到，为了更新 v′w v w ′ ，对于每一个训练实例，我们不得不迭代词汇表中的每一个单词 wj w j ，计算它们的网络输入 uj u j ，概率预测 yj y j （对于skip-gram，是 yc,j y c , j ），它们的预测误差 ej e j （对于skip-gram，是 EIj E I j ），最后计算它们的预测误差以更新输出向量 v′j v j ′ 。
给定一个训练样本，要对所有的单词进行这样的运算，花费非常高。因此，扩展到大词汇量和大词料库时，这样做不现实。为了解决这个问题，直观来说，对于每一个样本，要限制必须被更新的输出向量的数量。要达到这个要求，一个优雅的解法就是分层softmax，另一个是降采样。
两个技巧都只是优化更新输出向量的计算过程。我们的推导中，我们关注三个量：（1） E E ，新的目标函数，（2） ∂E∂h ∂ E ∂ h ，更新输入向量的后向传播的预测误差的加权和。

本文主要对word2vec的数学模型进行阐述，关于优化过程的详细数学推导，将作为另一篇文章。