8.房价预测基础线性回归

• 代码地址：appke/Los-House-Prices: 洛杉矶房价预测

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 忽略警告信息
import warnings
warnings.filterwarnings("ignore")

数据集的准备

train = pd.read_csv('datas/house_data.csv')
y = train['SalePrice']
train.shape

(1460, 82)

train1 = train.drop(['Id', 'SalePrice'], axis=1)
train1.shape

(1460, 80)

# 变成one_hot形式，内容全部被数字化了,原特征删除
X = pd.get_dummies(train1).reset_index(drop=True)
X.head()

	MSSubClass	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	BsmtFinSF2	...	SaleType_ConLw	SaleType_New	SaleType_Oth	SaleType_WD	SaleCondition_Abnorml	SaleCondition_AdjLand	SaleCondition_Alloca	SaleCondition_Family	SaleCondition_Normal	SaleCondition_Partial
0	60	65.0	8450	7	5	2003	2003	196.0	706	0	...	0	0	0	1	0	0	0	0	1	0
1	20	80.0	9600	6	8	1976	1976	0.0	978	0	...	0	0	0	1	0	0	0	0	1	0
2	60	68.0	11250	7	5	2001	2002	162.0	486	0	...	0	0	0	1	0	0	0	0	1	0
3	70	60.0	9550	7	5	1915	1970	0.0	216	0	...	0	0	0	1	1	0	0	0	0	0
4	60	84.0	14260	8	5	2000	2000	350.0	655	0	...	0	0	0	1	0	0	0	0	1	0

5 rows × 303 columns

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2, random_state=123)

X_train.shape

(1168, 303)

X_test.shape

(292, 303)

基础线性回归

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error #方差

lm=LinearRegression()

lm.fit(X_train, y_train)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
         normalize=False)

pred=lm.predict(X_test)

np.sqrt(mean_squared_error(np.log(y_test), np.log(pred)))

0.12627809622157107

np.sqrt(mean_squared_error(y_test, pred))

24973.913406557556

def benchmark(model):
    pred = model.predict(X_test)
    # 方差
    logrmse = np.sqrt(mean_squared_error(np.log(y_test), np.log(pred)))
    return logrmse

benchmark(lm)

0.12627809622157107

数据预处理 Preprocessing

先用机器学习参数去跑结果

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler

# 把机器学习方法，直接放进 make_pipeline
lm_model = make_pipeline(RobustScaler(), LinearRegression())

# 将数据变换后的数据，进行机器学习
lm_model.fit(X_train, y_train)

Pipeline(memory=None,
     steps=[('robustscaler', RobustScaler(copy=True, quantile_range=(25.0, 75.0), with_centering=True,
       with_scaling=True)), ('linearregression', LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
         normalize=False))])

# 评测模型
benchmark(lm_model)

0.1262780962215701

benchmark(lm)

0.12627809622157107

RidegeRegression

朴素的Ridge回归

from sklearn.linear_model import Ridge

ridge_model = Ridge(alpha=0.1)

ridge_model.fit(X_train, y_train)

Ridge(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver='auto', tol=0.001)

benchmark(ridge_model)

0.12658320875064985

数据预处理的Ridge回归

ridge_model_pipe=make_pipeline(RobustScaler(), Ridge(alpha=0.1))

ridge_model_pipe.fit(X_train, y_train)

Pipeline(memory=None,
     steps=[('robustscaler', RobustScaler(copy=True, quantile_range=(25.0, 75.0), with_centering=True,
       with_scaling=True)), ('ridge', Ridge(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver='auto', tol=0.001))])

benchmark(ridge_model_pipe)

0.12658566764241647

带有CV的Ridge回归

cross view data K折交叉

from sklearn.model_selection import KFold
from sklearn.linear_model import RidgeCV

kfolds=KFold(n_splits=10, shuffle=True, random_state=123)

r_alphas=[0.01, 0.1, 1, 3, 5, 7, 10, 100]

ridge_model_cv=make_pipeline(RobustScaler(), RidgeCV(alphas=r_alphas, cv=kfolds))

# RidgeCV()

ridge_model_cv.fit(X_train, y_train)

Pipeline(memory=None,
     steps=[('robustscaler', RobustScaler(copy=True, quantile_range=(25.0, 75.0), with_centering=True,
       with_scaling=True)), ('ridgecv', RidgeCV(alphas=array([1.e-02, 1.e-01, 1.e+00, 3.e+00, 5.e+00, 7.e+00, 1.e+01, 1.e+02]),
    cv=KFold(n_splits=10, random_state=123, shuffle=True),
    fit_intercept=True, gcv_mode=None, normalize=False, scoring=None,
    store_cv_values=False))])

benchmark(ridge_model_cv)

0.12385966794851841

def benchmark2(model, testset, label):
    pred=model.predict(testset)
    if pred[pred<0.].shape[0]>0:
        print('Neg Value') #拟合过程飞掉
    rmse=np.sqrt(mean_squared_error(label, pred))
    lrmse=np.sqrt(mean_squared_error(np.log(label), np.log(pred)))
    print('RMSE:', rmse)
    print('LRMSE:', lrmse)
    return lrmse

benchmark2(ridge_model_cv, X_test, y_test)

RMSE: 26907.89401651115
LRMSE: 0.12385966794851841

0.12385966794851841

r_alphas2=[.0001, .0003, .0005, .0007, .0009, .01, 0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 20, 30, 50, 60, 70, 80]

def ridge_train_test(alpha):
    m = make_pipeline(RobustScaler(), RidgeCV(alphas=[alpha], cv=kfolds))
    m.fit(X_train, y_train)
    return benchmark2(m, X_test, y_test)

ridge_train_test(.0001)

RMSE: 24973.969249187514
LRMSE: 0.12627904574538876

0.12627904574538876

# 要写很多很多野代码
scores=[]
for k in r_alphas2:
    scores.append(ridge_train_test(k))

# 每一个alpha 的表现情况
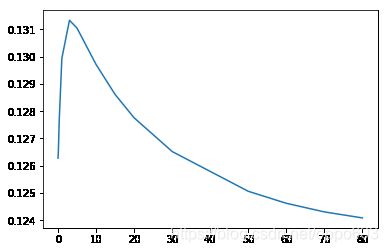
plt.plot(r_alphas2, scores)

[]

RidgeCV自动筛选参数

找到 alpha 最好的参数

# 从e-10,到e2.8 平均抽样150个
r_alphas3=np.logspace(-10, 2.8, 150)

scores=[]
for k in r_alphas3:
    scores.append(ridge_train_test(k))

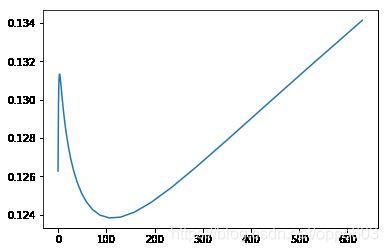
plt.plot(r_alphas3, scores)

[]

可以使用自动优化筛选出最优的alpha

ridge_model2 = make_pipeline(RobustScaler(), RidgeCV(
        alphas=r_alphas3, cv=kfolds
)).fit(X_train, y_train)

benchmark2(ridge_model2, X_test, y_test)

RMSE: 25983.546991372652
LRMSE: 0.12570253861398775

0.12570253861398775

ridge_model2.steps

[('robustscaler',
  RobustScaler(copy=True, quantile_range=(25.0, 75.0), with_centering=True,
         with_scaling=True)),
 ('ridgecv',
  RidgeCV(alphas=array([1.00000e-10, 1.21873e-10, ..., 5.17719e+02, 6.30957e+02]),
      cv=KFold(n_splits=10, random_state=123, shuffle=True),
      fit_intercept=True, gcv_mode=None, normalize=False, scoring=None,
      store_cv_values=False))]

# 最好的alpha
ridge_model2.steps[1][1].alpha_

39.56538865832277

和曲线得到的最优alpha不一样？

• 图表示全部是测试集，最好的alpha
• 自动化筛选，是不知道测试集合的分布的
  • 既参考了训练集的均值、方差、loss，也考虑了模型复杂度，挑出来是最优的
  • steps[1][1].alpha_ 更科学
• 单把20%数据当测试集是不对的，比赛时不根本不知道评测集

LassoRegression

带有CV的Lasso回归

from sklearn.linear_model import LassoCV

l_alphas=np.logspace(-10, 2.8, 150)

def lasso_train_test(alpha):
    lasso_model = make_pipeline(RobustScaler(), LassoCV(alphas=[alpha], cv=kfolds))
    lasso_model.fit(X_train, y_train)
    lrmse = benchmark2(lasso_model, X_test, y_test)
    return lrmse

scores = []
for k in l_alphas:
    print("Alpha:", k)
    scores.append(lasso_train_test(k))

plt.plot(l_alphas, scores)

[]

lasso_train_test(50)

RMSE: 24601.931715190687
LRMSE: 0.11575377693141331

0.11575377693141331

LassoCV自动筛选参数

lasso_model2=make_pipeline(RobustScaler(), LassoCV(
    alphas=l_alphas, cv=kfolds
)).fit(X_train, y_train)

benchmark2(lasso_model2, X_test, y_test)

RMSE: 25431.111829508853
LRMSE: 0.12203176481488645

0.12203176481488645

lasso_model2.steps[1][1].alpha_

192.5589718453296

ElasticNet

带有CV的ElasticNet回归

from sklearn.linear_model import ElasticNetCV

e_l1ratio = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.85,0.9,0.95,1]

e_alphas = l_alphas

def elastic_train_test(alpha, l1ratio):
    e_model = make_pipeline(RobustScaler(), ElasticNetCV(
        alphas=[alpha], l1_ratio=[l1ratio]
    )).fit(X_train, y_train)
    lrmse = benchmark2(e_model, X_test, y_test)
    return lrmse

elastic_train_test(50,0.5)

RMSE: 64803.88956616406
LRMSE: 0.3056812482960621

0.3056812482960621

ElasticNetCV自动筛选参数

elastic_model2 = make_pipeline(RobustScaler(), ElasticNetCV(
    alphas=e_alphas, l1_ratio=e_l1ratio
)).fit(X_train,y_train)

benchmark2(elastic_model2, X_test, y_test)

RMSE: 25431.111829508853
LRMSE: 0.12203176481488645

0.12203176481488645

elastic_model2.steps[1][1].alpha_

192.5589718453296

elastic_model2.steps[1][1].l1_ratio_

1.0