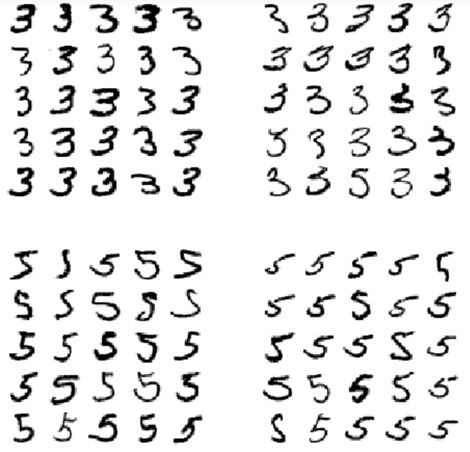分类问题（五）误差分析

误差分析

如果上一章中的分类器是一个真实的项目，则我们最好是要遵循机器学习项目步骤：探索数据、准备数据、尝试多个模型、列出表现最好的几个模型、使用GridSearchCV对超参数进行调优、尽可能实现自动化。现在，假设我们已经有了一个性能还不错的模型，接下来我们要找一些办法去优化、提升它。其中一个办法是就分析这个模型产生的各种不同类型的误差、差错。

首先我们看一下混淆矩阵，我们需要先使用cross_val_predict() 做预测，然后调用confusion_matrix() 计算：

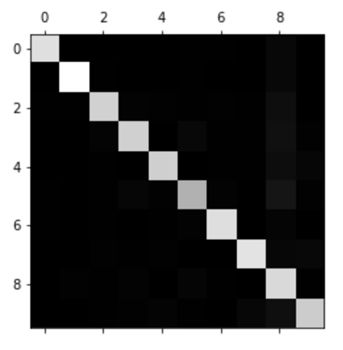
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
>array([[5576,    0,   21,    6,    9,   43,   37,    6,  224,    1],
       [   0, 6398,   38,   23,    4,   44,    4,    8,  213,   10],
       [  26,   27, 5242,   90,   71,   26,   62,   36,  371,    7],
       [  24,   17,  117, 5220,    2,  208,   28,   40,  405,   70],
       [  12,   14,   48,   10, 5192,   10,   36,   26,  330,  164],
       [  28,   15,   33,  166,   55, 4437,   76,   14,  538,   59],
       [  30,   14,   41,    2,   43,   95, 5560,    4,  128,    1],
       [  21,    9,   52,   27,   51,   12,    3, 5693,  188,  209],
       [  17,   63,   46,   90,    3,  125,   25,   10, 5429,   43],
       [  23,   18,   31,   66,  116,   32,    1,  179,  377, 5106]])

 

可以看到有很多的数字，为了方便一般我们会将这种混淆矩阵以图片的方式展示出来，使用Matplotlib 的matshow() 方法：

plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()

这个混淆矩阵看起来还不错，因为图片基本都在主对角线上，也就是说它们被正确地分类到的所属的类别。其中第5个的颜色相较其他数字稍深，说明可能有两种问题：

1. 数字5的图片在数据集中较少
2. 模型在数字5上的表现不如在其他数字上好

事实上我们可以确认这两种问题都存在。

下面我们将关注点放在误差上。首先我们需要将混淆矩阵中的每个值均除以对应类别的总数，用来对比误差率（之前的混淆矩阵中，全部是精确的错误数，并不容易进行观察与判断）：

row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx/row_sums

 

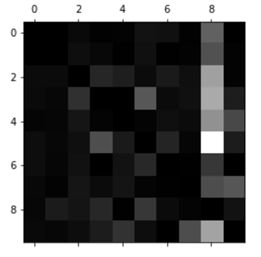
然后我们将主对角线填充0，仅保留误差，最后画出结果：

np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()

 

现在我们可以明显地看到分类器产生的误差。这里回顾一下，行代表的是实际类别，列代表的是预测类别。可以明显地看到第8列非常亮，它告诉我们的是：很多图片被错误地分类成了数字8。然而，第8行却并不差，说明：数字8一般都被正确地分类为了数字8。在图中还可以看到混淆矩阵并不一定对称。还可以看到数字3与数字5经常被混淆（行列均是），将数字3预测为数字5，并将数字5预测为数字3。

通过分析混淆矩阵，经常可以给我们提供一个更深层的视角观察模型表现，并提供我们提升模型的思路。在上图中，我们似乎需要将更多的精力花在减少错误预测的数字8（false 8）。例如，我们可以获取更多的看起来像数字8但不是数字8的训练数据，这样可以让分类器学习如何将它们与真正的数字8区分开来。或者也可以构造一些新的属性帮助分类器，例如，写一个算法，计算回环的数目（例如，8有两个，6有一个，5没有）。或者可以对图片进行预处理（例如用sk-image，pillow，或OpenCV），让一些模式更突出的显示出来（例如回环）。

分析单独的各个误差也是一个很好的办法，它可以告诉我们分类器做了什么，并且为什么分类失败。不过这个过程会更难，并且更耗时。例如，我们可以画出一些数字3与数字5：

def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    plt.axis("off")

def plot_digits(instances, images_per_row=10, **options):
    size = 28
    images_per_row = min(len(instances), images_per_row)
    images = [instance.reshape(size,size) for instance in instances]
    n_rows = (len(instances) - 1) // images_per_row + 1
    row_images = []
    n_empty = n_rows * images_per_row - len(instances)
    images.append(np.zeros((size, size * n_empty)))
    for row in range(n_rows):
        rimages = images[row * images_per_row : (row + 1) * images_per_row]
        row_images.append(np.concatenate(rimages, axis=1))
    image = np.concatenate(row_images, axis=0)
    plt.imshow(image, cmap = mpl.cm.binary, **options)
    plt.axis("off")

cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]

plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()

 

左边的两个5×5 的图展示的是被预测为“数字3“的图，右边的两幅5×5的图显示的是被预测为”数字5“的图。左下角与右上角的两幅5×5的图均是分类错误的图片。从这些图可以看出，分类器在分类某些图片的时候，确实受到了手写不规范的影响（例如左下角第1行第2列那个5，即使是人为分辨，也难以分辨为5还是3）。然而，除了少部分手写的不清晰外，其他大部分的数字是能够人为分辨的，所以光看图很难理解为什么分类器在这些数字上分类错误。其实它的原因是由于我们使用了一个简单的SGDClassifier，它是一个线性模型。它做的事是：给每个像素点分配一个权重，在它看到一张新图片时，它仅会将所有带权的像素点强度累加起来，最后会为每个类别生成一个分数。所以，由于数字3与数字5的像素点相差的不多，这个模型会很容易将它们混淆。

3与5的主要区别是连接上方横线与下方湾沟的那条短线。如果我们在写一个3时，把这条短线稍微靠了左边，那这个分类器可能就会将它分类成5，反之亦然。换句话说，这个分类器对图片的平移与旋转非常敏感。所以其中一个减少3与5混淆不清的方法是预先处理图片，并确保它们在正中间，且没有旋转。这个可能会对减少误差有所帮助。