GMC: Graph-based Multi-view Clustering 论文笔记
GMC: Graph-based Multi-view Clustering(TKDE2019)
论文链接:https://ieeexplore.ieee.org/abstract/document/8662703/
1. 论文主要贡献
提出了一种通用的基于图的multi-view聚类方法(GMC),用于解决现有方法的一些限制。GMC自动加权每个视图,共同学习每个视图的图和融合图,并在融合后立即生成最终簇,不需要引入另外的spectral聚类方法,值得注意的是,每个视图图的学习和融合图的学习可以互相增强。
2. 论文主要内容
2.1 Introduction
这里主要提及了现有的一些基于图的multi-view聚类方法的限制,主要有三点:
◆ 在一些方法中并未考虑不同view的重要性的差异——融合过程中权重问题;
◆ 许多现有方法都需要额外的聚类步骤以在融合后产生最终的聚类;
◆ 目前大多数方法都是单独构造每个视图的图,并在融合过程中将构造的图固定下来。
针对上述三点限制,本文提出了相应的解决方案:
◆ 自动生成权重w;
◆ 通过对图的拉普拉斯矩阵施加秩约束,自动生成聚类结果;
◆ 本文提出的方法以互相增强的方式共同构造每个视图图和融合图,此处的互相增强是从最终目标函数中体现出来的,后面将会介绍。
2.2 Related Work
这部分内容我认为作者写的一般,在这里我总结一下图聚类,谱聚类。
基于图的聚类:这里的图指的是图结构G(V,E),而不是图像。
图的表示:G(V,E)表示无向图,V是顶点集,表示样本点,E是边集,边上的权重w_ij表示样本点i与j的相似度。
图聚类:基于图的聚类可以看作图G的划分,将G按照一定的准则划分成一系列互不相交的子图G1,G2,G3…;
损失函数:Cut(G1,G2)= ∑_(i∈G1,j∈G2)▒w_ij ,目标在于付出最小的代价将G划分成为G1,G2.
谱聚类:与基于图的聚类的区别在于,谱聚类通常会先找到数据的低维嵌入表示,然后对这种嵌入表示执行聚类算法(e.g. K-means)以生成最终聚类。谱聚类的关键在于找到图的表示,一般流程为[1]:
◆ 确定相似性度量准则,得到相似性矩阵W;
◆ 计算图的拉普拉斯矩阵L=D-W,D是一个对角度矩阵;
◆ 计算L前k个最小特征值对应的特征向量,作为节点的向量表示; ◆ 运用聚类算法得出聚类结果。
2.3 GMC
GMC由三部分构成,SIG Matrix Construction,Multiple Data Graph Fusion,Laplacian Rank Constraint. 先看一下GMC的最终目标函数,然后联系这三个部分。
目标函数:
(1)
其中,m, n分别表示视图数与样本点数;Sv表示第v个视图的相似度诱导矩阵——the similarity-induced graph (SIG),就是相似度矩阵的稀疏表示;sijv表示在第v个视图样本的i与样本点j的相似度;U表示fusion graph matrix;wv表示第v个视角的权重;Lu是U的拉普拉斯矩阵;F是一个辅助矩阵是由U的特征向量组成。
Eq.(1)中,第一项与第二项是从data matrix X计算出similarity-induced graph;第二项是一个先验,如果仅关注Eq.(1)的第二项,则可以将先验视为每个数据点与xiv的相似度值,即1/n;约束条件1Tsiv=1相当于约束Sv是稀疏的,因为假如只考虑xi的最近样本点xj,则sijv=1,其余全部为0;
Eq.(1)的第三项是Multiple Data Graph Fusion,wv表示第v个视角的权重;可以看出,每个SIG矩阵S1,…,Sm和矩阵U的学习被合并为一个联合问题,于是两者的学习可以自然地互相帮助,互相增强。
Eq.(1)的第四项是对Lu施加秩约束,学习到F的每一列就是聚类中心向量表示,源自一个重要理论:
Theorem 2. The multiplicity r of the eigenvalue 0 of the Laplacian matrix LU is equal to the number of connected components in the graph of the unified matrix U. ——拉普拉斯矩阵LU的特征值0的多重性r等于统一矩阵U的图中连通分量的数量。
GMC流程:data matrix —>(similarity matrix)—> SIG(similarity-induced graph)<—>U(unified matrix)—>clustering result.
采用交替优化的方式优化求解Sv,Wv,U,F。
2.4 实验设置
实验环境:Windows Server 2008 R2 with Intel Xeon processor, 24GB RAM and MATLAB development environment.
数据集:
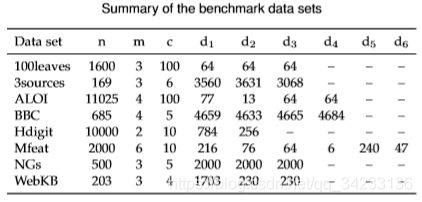
n:样本数;m:视角数;c:聚类数;di:第i个视角维度
Baseline:
SK-means: Single view K-means
SNcut: Single view Normalized cut
MKC: Multi-view Kmeans Clustering
MultiNMF: Multi-view clustering via Non-negative Matrix Factorization
CoregSC: Co-regularized Spectral Clustering
MSC: Multi-view Spectral Clustering
ASMV: Adaptive Structure-based Multi-view clustering
MGL: Multiple Graph Learning
MCGL: Multi-view Clustering with Graph Learning
Evaluation:
ACC; NMI; ARI(adjusted rand index); F1 measure.
参考:
[1]. https://blog.csdn.net/u010865478/article/details/82750440