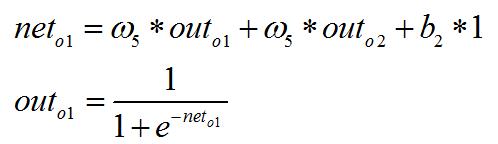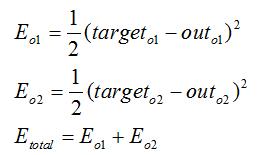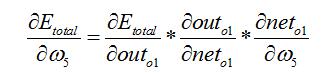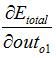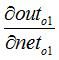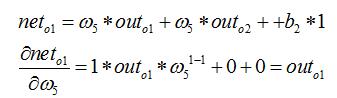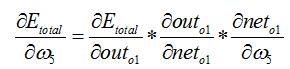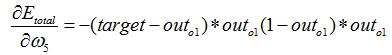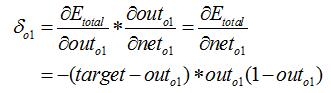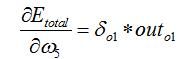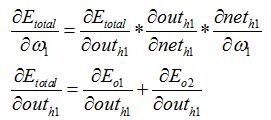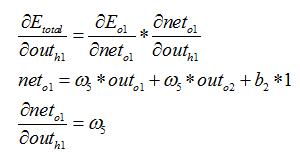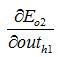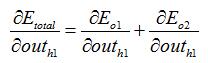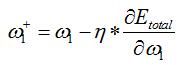模式识别学习——人工神经网络——BP算法

1、主要工作

     自行编写代码完成BP神经网络设计男女生分类器；

2、工作具体内容

2.1 BP算法简介

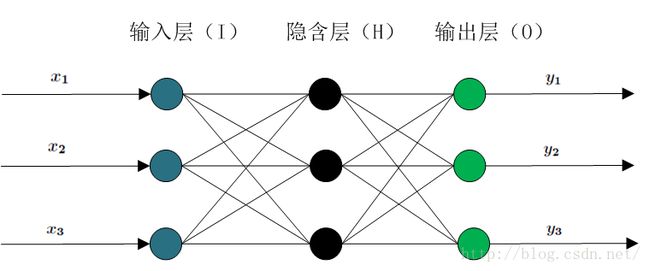
      BP（Back Propagation）网络是1986年由Rinehart和McClelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)（如图2.1所示）。

图2.1 BP神经网络模型拓扑结构

    BP算法由数据流的前向计算（正向传播）和误差信号的反向传播两个过程构成。正向传播时，传播方向为输入层→隐层→输出层，每层神经元的状态只影响下一层神经元。若在输出层得不到期望的输出，则转向误差信号的反向传播流程。通过这两个过程的交替进行，在权向量空间执行误差函数梯度下降策略，动态迭代搜索一组权向量，使网络误差函数达到最小值，从而完成信息提取和记忆过程。

2.2 BP算法基本原理

    输入信号Xi通过中间节点（隐层点）作用于输出节点，经过非线形变换，产生输出信号Yk，网络训练的每个样本包括输入向量X和期望输出量t，网络输出值Y与期望输出值t之间的偏差，通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度Tjk以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

2.3 BP算法基本步骤

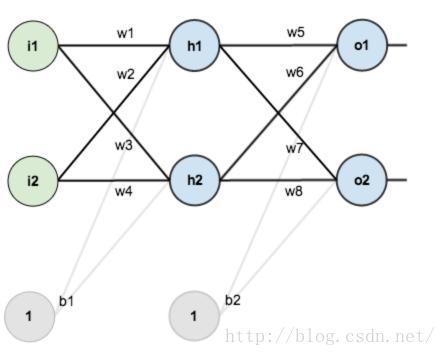
    假设，你有这样一个网络层：

图2.2 BP神经网络网络层示例

    第一层是输入层，包含两个神经元i1，i2，和截距项b1；第二层是隐含层，包含两个神经元h1,h2和截距项b2，第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数我们默认为sigmoid函数。

      Step 1 前向传播

      1.输入层---->隐含层：

   计算神经元h1的输入加权和：

     神经元h1的输出o1:(此处用到激活函数为sigmoid函数)：

    同理，可计算出神经元h2的输出o2：

       2.隐含层---->输出层：

    计算输出层神经元o1和o2的值：　

    同理，可计算出神经元o2：

    这样前向传播的过程就结束了，现在我们对误差进行反向传播，更新权值，重新计算输出。

       Step 2 反向传播

       1.计算总误差

    总误差：(square error)

    但是有两个输出，所以分别计算o1和o2的误差，总误差为两者之和：

        2.隐含层---->输出层的权值更新：

    以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）

 

       下面的图可以更直观的看清楚误差是怎样反向传播的：

 

       现在我们来分别计算每个式子的值：

       计算：

       计算：

 

       计算：

       最后三者相乘：

    这样我们就计算出整体误差E(total)对w5的偏导值。

       回过头来再看看上面的公式，我们发现：

       为了表达方便，用来表示输出层的误差：

    因此，整体误差E(total)对w5的偏导公式可以写成：

    最后我们来更新w5的值：

     （其中，是学习速率）。

    同理，可更新w6,w7,w8。

       3.隐含层---->隐含层的权值更新：

    方法其实与上面说的差不多，但是有个地方需要变一下，在上文计算总误差对w5的偏导时，是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时，是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差，所以这个地方两个都要计算。

 

 

       先计算：

 

      同理，计算出：

　

      两者相加得到总值：

      再计算：

 

      再计算：

      最后，三者相乘：

   最后，更新w1的权值：

   同理，额可更新w2,w3,w4的权值：。

 

　　这样误差反向传播法就完成了，最后我们再把更新的权值重新计算，不停地迭代，直至总误差E(total)降低到一定值以内，训练结束。

2.4 代码

（1）前向传播：qianxiang.m

%-------------------qiangxiang.m----------------------------%
%前向传播函数
function[O2,O3]=qianxiang(O1,w1,w2)    %前向传播算法
 
for i=1:5  
    O2(i) = sigmoid(sum(O1 .* w1(i,:)));%暂时不加偏置
end
    O3 = sigmoid(sum(O2 .* w2));
end

（2）后向传播：houxiang.m 

%-------------------houxiang.m----------------------------%
%后向传播函数
function[w1,w2]=houxiang(y,O1,O2,O3,w1,w2)  %后向传播算法
eta=0.5;
g3 = O3 - y;
f3 = O3 * (1 - O3);
deltaO = g3 * f3;
 
for i = 1:5
    w2(i) = w2(i) - eta * deltaO * O2(i);
end
for i = 1:5
    f2(i) = O2(i) * (1 - O2(i));
    for j = 1:5     
        deltaH(i,j) = f2(i) * deltaO * w2(i);
        w1(i,j) = w1(i,j) - eta * deltaH(i,j) * O1(j);
    end
end

（3）归一化函数：uniform.m 

 %-------------------uniform.m----------------------------%
%归一化函数
function [g] = uniform(x)
    a = max(x);
    b = min(x);
    d = a - b;
    g = (x - b) / d;
end

（4） sigmoid函数：sigmoid.m 

%-------------------sigmoid.m----------------------------%
%sigmoid函数
function z=sigmoid(x)
    %z=sigmf(x,[1 0]);
    z = 1 / (1 + exp(-x));
End

（5） auc计算函数：auc.m 

%-------------------auc.m----------------------------%
%auc计算函数
function [result]=auc(test_targets,output)  
%test_targets为原始样本标签,output为分类器得到的标签  
%均为行或列向量  
[A,I]=sort(output);  
M=0;N=0;  
for i=1:length(output)  
    if(test_targets(i)==1)  
        M=M+1;  
    else  
        N=N+1;  
    end  
end  
sigma=0;  
for i=M+N:-1:1  
    if(test_targets(I(i))==1)  
        sigma=sigma+i;  
    end  
end  
result=(sigma-(M+1)*M/2)/(M*N); 

（6）主程序：homework2.m

%数据初始化
[n1] =  xlsread('样本数据');
S = 149;
L = 75;
height = n1(:,4);
weight = n1(:,5);
Uh = uniform(height);
Uw = uniform(weight);
w1 = [0.2 0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2 0.2 ;0.2 0.2 0.2 0.2 0.2 ;0.2 0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2 0.2 ];
w2 = [0.2,0.2,0.2,0.2,0.2 ];
critical = 0.04;
error = 0; 
for i = 1:L              %以样本数据的前L项作为训练集
    y = n1(i,2);
    O1 = [Uh(i),Uw(i),n1(i,7),n1(i,8),n1(i,9)];
    %前向传播
    [O2,O3] = qianxiang(O1,w1,w2);
    error(i) = ((y - O3)^2) / 2;%样本的误差累加
    
    %在需要时进行后向传播修正权值
     if error(i) < critical      %当前误差是否小于阈值
         if max(error) < critical %是否全部误差都小于阈值
             break;
         end          
     else
        [w1,w2] = houxiang(y,O1,O2,O3,w1,w2);%若不满足条件则继续反向传播
     end
end
disp(max(error));
%以后(S - L)项作为测试集，导出测试集样本标签并与测试集分类结果做比较
for i = (L + 1):S
 y2 = n1(i,1);
    O1 = [Uh(i),Uw(i),n1(i,7),n1(i,8),n1(i,9)];
    [O2,O3] = qianxiang(O1,w1,w2);
    pp(i - L,1) = O3;              %pp为测试集分类结果
end
 
for j = 1:(S - L)
    ppp(j,1) = n1(j + L,2);       %ppp为测试集样本标签 
end
s1 = 0;
for k = 1:(S - L)
    if abs(ppp(k,1) - pp(k,1)) < 0.5
        s1 = s1 + 1;
    end
end
acc1 = s1/(S - L);
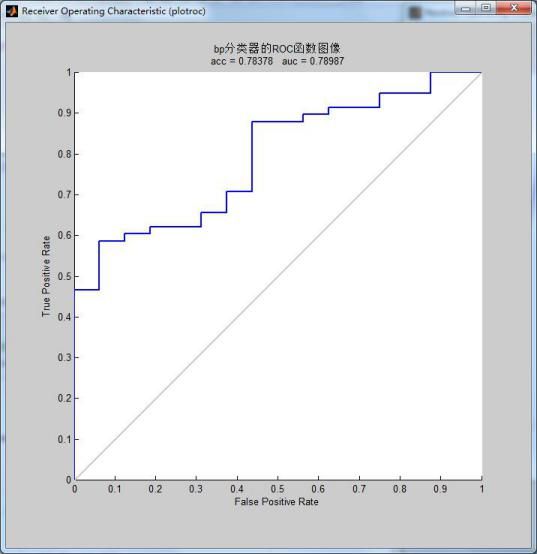
%bp分类器的acc，auc和roc图像
figure(1)
plotroc(ppp.',pp.');
A = auc(ppp.',pp.');  
title({'bp分类器的ROC函数图像';['acc = ' num2str(acc1),'   auc = ' num2str(A)]},'fontsize',10); 

2.5分类结果：

图2.5 BP算法分类结果

附录：

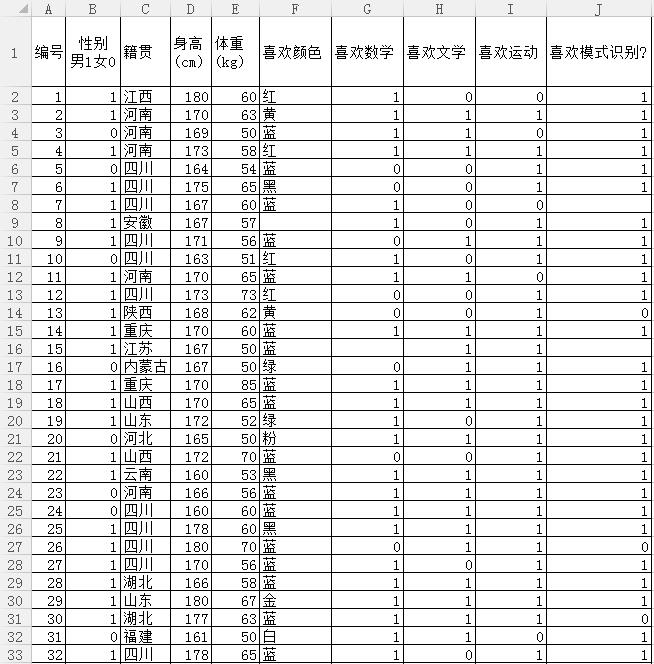
数据节选：