2016湘潭邀请赛 xtu1250

Super Fast Fourier Transform

Accepted : 67		Submit : 354
Time Limit : 2000 MS		Memory Limit : 65536 KB

Super Fast Fourier Transform

Bobo has two sequences of integers {a1,a2,…,an} and {b1,b2,…,bm}. He would like to find

∑i=1n∑j=1m⌊|ai−bj|−−−−−−−√⌋.

Note that ⌊x⌋ denotes the maximum integer does not exceed x, and |x| denotes the absolute value of x.

Input

The input contains at most 30 sets. For each set:

The first line contains 2 integers n,m (1≤n,m≤105).

The second line contains n integers a1,a2,…,an.

The thrid line contains m integers b1,b2,…,bm.

(ai,bi≥0,a1+a2+⋯+an,b1+b2+…,bm≤106)

Output

For each set, an integer denotes the sum.

Sample Input

1 2
1
2 3
2 3
1 2
3 4 5

Sample Output

2
7

题解：

因为(ai,bi≥0,a1+a2+⋯+an,b1+b2+…,bm≤106)         (1≤n,m≤105).

可以知道重复的数字很多

极端小的情况：平均每个数字为10

极端大的情况：平均每个数字为十的六次方

故知重复的数字很多

#include
#include
#include
#include
using namespace std;

#define mem(arr) memset(arr,0,sizeof(arr))
#define LL long long
#define N 100005
int a[N],b[N],c[N];
int k1[N],k2[N];

int main()
{
    int n,m;
    //freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        mem(k1),mem(k2);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            c[i]=a[i];
        }
        sort(a+1,a+1+n);
        int cnt1=unique(a+1,a+1+n)-(a+1);///去重后的数组长度
        for(int i=1;i<=n;i++)
            ++k1[lower_bound(a+1,a+1+cnt1,c[i])-a];///计算数组c各个数字出现的频率
            ///lower_bound(a+1,a+1+cnt1,c[i])-a  表示这个数字在数组a中的位置

        for(int i=1;i<=m;i++){
            scanf("%d",&b[i]);
            c[i]=b[i];
        }
        sort(b+1,b+1+m);
        int cnt2=unique(b+1,b+1+m)-(b+1);
        for(int i=1;i<=m;i++)
            ++k2[lower_bound(b+1,b+1+cnt2,c[i])-b];

        LL ans=0;
        for(int i=1;i<=cnt1;i++){
            for(int j=1;j<=cnt2;j++){
                LL tmp=sqrt(abs(a[i]-b[j]));
                ans+=k1[i]*k2[j]*tmp;
            }
        }
        printf("%I64d\n",ans);
    }
    return 0;
}

unique函数是一个去重函数

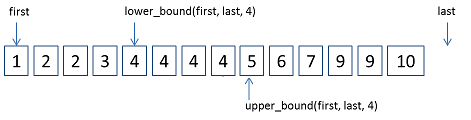
ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置

ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置

     lower_bound和upper_bound如下图所示：

 

int lower_bound(int *array, int size, int key)
{
    int first = 0, middle;
    int half, len;
    len = size;

    while(len > 0) {
        half = len >> 1;
        middle = first + half;
        if(array[middle] < key) {     
            first = middle + 1;          
            len = len-half-1;       //在右边子序列中查找
        }
        else
            len = half;            //在左边子序列（包含middle）中查找
    }
    return first;
}

int upper_bound(int *array, int size, int key)
{
    int first = 0, len = size-1;
    int half, middle;

    while(len > 0){
        half = len >> 1;
        middle = first + half;
        if(array[middle] > key)     //中位数大于key,在包含last的左半边序列中查找。
            len = half;
        else{
            first = middle + 1;    //中位数小于等于key,在右半边序列中查找。
            len = len - half - 1;
        }
    }
    return first;
}