HDU 4587 (割点)

TWO NODES

Time Limit: 24000/12000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 1618    Accepted Submission(s): 502

Problem Description

Suppose that G is an undirected graph, and the value of  stab is defined as follows:

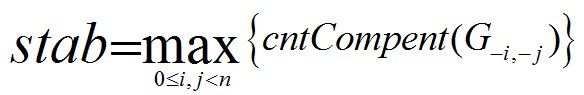
Among the expression,G _{-i, -j} is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes.  cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of  stab.

 

Input

The input will contain the description of several graphs. For each graph, the description consist of an integer N for the number of nodes, an integer M for the number of edges, and M pairs of integers for edges (3<=N,M<=5000).
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.

 

Output

For each graph in the input, you should output the value of  stab.

 

Sample Input

4 5 0 1 1 2 2 3 3 0 0 2

 

Sample Output

2

 

题意:求一个图去掉两个点之后的最多的联通分量数.

首先枚举一个去掉的点,然后求出所有的割点,对于所有的割点,他能够遍历到的点并

且没有访问过的点数就是删去他能够增加的联通分量数.

坑点:

注意树根和孤立节点的情况.

#include 
#include 
#include 
#include 
#include