数据结构与算法(8):前缀表达式(波兰表达式),中缀表达式,后缀表达式(逆波兰表达式:实例逆波兰计算器)
一:前缀表达式的计算机求值
从右到左扫描表达式,遇到了数字,就将数字压入堆栈,遇到运算符就将运算符压入堆栈,弹出栈顶的两个数,用运算符对他们做相应的计算.(栈顶元素,和次顶元素).并将结果入栈,接着重复上述的过程指导表达式的最左端,最后运算得出的值即为表达式的结果
举个例子:(3+4)*5-6对应的前缀表达式就是-*+3456,针对前缀表达式求值步骤如下:
- 从右到左进行扫描,将6543依次压入栈中
- 遇到
+运算符后弹出3和4(3为栈顶一个元素,4为次顶元素),计算出3+4的值后,得到的7压入栈中. - 接下来是
*,因此弹出7和5,这样计算出结果35,压入栈中 - 最后是
-运算符,计算的35-6的29,由此雨中结果为29
二:中缀表达式
- 中缀表达式就是常见的运算表达式
- 中缀表达式的求值是最我们人最熟悉的,但是对计算机来说却不好操作.因此,在计算结果时,往往会将中缀表达式转换成其他表达式来操作,一般是转成后缀表表达式
三:后缀表达式
- 后缀表达式又称为逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
- 举个例子,(3+4)*5-6的后缀表达式就是
3 4 + 5 * 6 -
应用实例:逆波兰计算器,
任务:
- 输入一个逆波兰表达式,使用栈计算其结果
- 支持小括号和多位数整数,计算器只支持对整数进行计算
代码演示:
package com.qiu.stack;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class PolandNotation {
public static void main(String[] args) {
//先定义一个逆波兰表达式
String suffixExpression = "3 4 + 5 * 6 - ";//为了方便,逆波兰表达式的数字和符号用空格隔开
//1.先将 suffixExpression=>放到一个arrayList中
//2.将ArrayList传递给一个方法,配合栈完成计算
List<String> list = getListString(suffixExpression);
System.out.println(list);
int res = calculate(list);
System.out.println(res);
}
//将逆波兰表达式依次将数据和运算符放入到arraylist中
public static List<String> getListString(String suffixExpression){
//将suffixExpression分割
String[] splits = suffixExpression.split(" ");
ArrayList<String> arrayList = new ArrayList<>();
for (String ele : splits){
arrayList.add(ele);
}
return arrayList;
}
//完成对逆波兰表达式的扫描,也就是遍历
public static int calculate(List<String> list){
//创建一个栈,只需要一个栈即可
Stack<String> stack = new Stack<>();
//遍历list
for (String items :list){
//使用正则表达式取出数
if (items.matches("\\d+")){
//匹配的是多位数
//入栈
stack.push(items);
}else{
//pop两个数,运算,再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res =0;
if (items.equals("+")){
res = num1+num2;
}else if (items.equals("-")){
res = num1-num2;
}else if (items.equals("*")){
res = num1*num2;
}else if (items.equals("/")){
res =num1/num2;
}else{
throw new RuntimeException("运算符有误!");
}
//把res入栈
stack.push(""+res);
}
}
//最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}
后缀表达式是适合计算机进行运算的,但是对人来说却不太友好,在一个表达式特别长的情况下会显得十分难受,所以在开发中一般都输入中缀表达式,然后再通过程序将中缀表达式转换成后缀表达式,供计算机执行
具体步骤如下
-
初始化两个:运算符栈s1和储存中间结果的栈s2
-
从左到右扫描中缀表达式
-
遇到操作数的时候,将其压入s2
-
遇到操作符(
+-*/())的时候,比较其与s1栈顶运算符的优先级
(1) 如果运算符栈s1为空,或栈顶运算符为左括号"(" 则直接将此运算符入栈;(2)否则,若优先级比栈顶运算符高,也将运算符压入s1;
(3)否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中的新的栈顶运算符相比较)
(4)遇到括号时:
如果是左括号“(”，则直接压入s1
如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
(5)重复步骤2至5，直到表达式的最右边
(6)将s1中剩余的运算符依次弹出并压入s2
(7)依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式
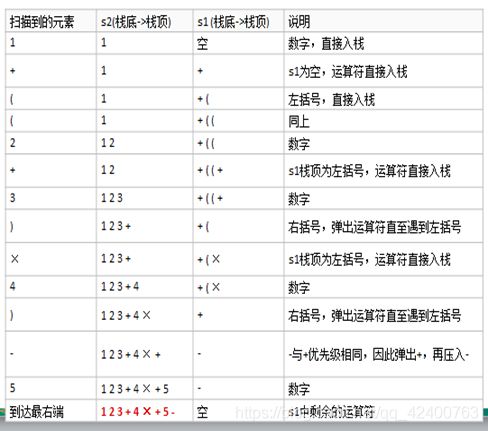
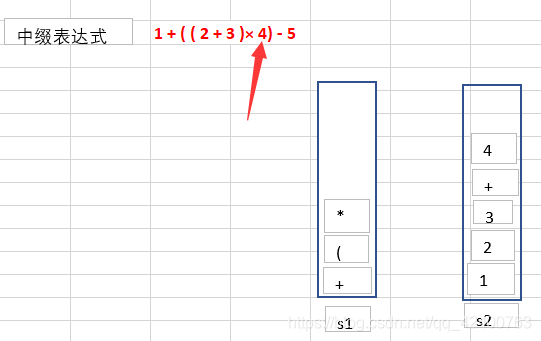
画一个示意图解释一下
第一步:扫描到了数字1时,直接放入栈s2中去,
第二步:扫描到了+,这个时候我们看s1中是否有运算符,这里我们看到s1中并没有数据,所以我们将运算符放在s1中
第三步:扫描到了(,根据步骤5.1.遇到了左括号,直接压入s1中
第四步:还是左括号,继续压入s1栈中
第五步:扫描到了数字,将其压入s2中
第六步:扫描到了+号,运算符的栈顶为(,所以直接将操作符压入s1中去
第七步:扫描到了数字3,所以直接压入s2中
重点来了!
第八步:我们遇到了右括号),所以我们依次弹出s1的运算符,并压入s2中去,同时抵消一个左括号
第九步:继续向下扫描,遇到了*,由于栈顶元素是左括号,不做比较.所以*直接入栈s1
第十步:扫描到了数字4,直接入s2栈
第十一步:扫描到了右括号,我们需要弹出s1中的运算符到s2中,知道遇到了左括号,并将其抵消
第十二步:扫描到了一个减法-,这个时候我们就比较栈s1中的栈顶运算符,由于栈顶中有符号+,和扫描到的运算符优先级相同,所以我们将s1栈顶的运算符弹出,并雅压入到s2中去,符号-,则入栈s1
第十三步:扫描到了数字,则直接压入s2中
第十四步:由于,表达式扫描完毕了,将s1中剩余的符号,依次压入到s2中
最后一步:依次弹出s2中的元素,并进行输出,结果的逆序即为中缀表达式对应的后缀表达式
代码实现:
package com.qiu.stack;
import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;
import org.omg.CORBA.PRIVATE_MEMBER;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class PolandNotation {
public static void main(String[] args) {
//完成将一个中缀表达式转成一个后缀表达式的功能
//1 + ( ( 2 + 3 )× 4) - 5 转成1 2 3 + 4 * + 5 -
//2.因为直接对一个字符串操作不方便,所以我们先将这个字符串以中缀的表达式对应的list
//3.就是说1 + ( ( 2 + 3 )× 4) - 5 转换成了一个ArrayList[1, +,( +(, 2, +, 3, ......]
//4.上述功能完成之后,我们将得到的中缀的表达式,转成一个后缀表达式对应的list,中缀的表达式中的list中的括号还是被消除掉了
String expression = "1+((2+3)*4)-5";
List<String> list = toInfixExpressionList(expression);
System.out.println("中缀表达式对应的list:"+list);
List<String> parseSuffixExpressionList = parseSuffixExpressionList(list);
System.out.println("后缀表达式对应的list:"+parseSuffixExpressionList);
System.out.printf("expression=%d",calculate(parseSuffixExpressionList));
/*
//先定义一个逆波兰表达式
String suffixExpression = "3 4 + 5 * 6 - ";//为了方便,逆波兰表达式的数字和符号用空格隔开
//1.先将 suffixExpression=>放到一个arrayList中
//2.将ArrayList传递给一个方法,配合栈完成计算
List list = getListString(suffixExpression);
System.out.println(list);
int res = calculate(list);
System.out.println(res);
*/
}
//方法:将中缀表达式转成后缀表达式
public static List<String> parseSuffixExpressionList(List<String> ls){
//定义两个栈s1 s2
Stack<String> s1 = new Stack<>();
//由于s2是一直在添加字符,没有pop操作,而且需要逆序输出,直接使用list避免麻烦
// Stack stack2 = new Stack<>();
List<String> s2 = new ArrayList<>();
//开始遍历ls
for (String item :ls){
//如果是一个数,加入到s2中
if(item.matches("\\d+")){
s2.add(item);
}else if (item.equals("(")){
s1.push(item);
}else if (item.equals(")")){
//我们需要弹出s1中的运算符到s2中,知道遇到了左括号,并将其抵消
while(!s1.peek().equals("(")){
s2.add(s1.pop());
}
s1.pop();//将这个左括号弹出去
}else {
//当item的运算符的优先级小于等于s1栈顶的运算符的优先级
//将s1栈顶的运算符弹出并压入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较；
//并且我们需要一个比较优先级的方法
while(s1.size()!= 0 && Operation.getValue(s1.peek())>=Operation.getValue(item)){
s2.add(s1.pop());//这里的意思就是说我们在栈顶操作符的优先级大于了扫描到的运算符优先级,那就将这个栈顶元素添加到s2中去
}
//还需要将item压入栈s1中
s1.push(item);
}
}
//将s1中剩余的元素弹出并压入到s2中去
while(s1.size()!= 0){
s2.add(s1.pop());
}
return s2;//因为是存放到list中的,list是有序的,因此按顺序输出就是对应的逆波兰表达式
}
//将中缀表达式转换成对应的list
public static List<String> toInfixExpressionList(String s){
// s:就是传进来的字符串
//定义一个list存放非中缀表达式,对应的内容
ArrayList<String> ls = new ArrayList<>();
int i = 0;//这个是一个指针,用于遍历中缀表达式字符串
String str;//对多位数的一个拼接工作
char c;//每遍历一个字符就放入到c中
do {
//如果c是一个非数字,我们就需要加入到这个ls中去,因为遍历到的可能不是一个非数字的话那就是/*-+,或者()
if ((c =s.charAt(i))<48 || (c = s.charAt(i)) > 57){
ls.add(""+c);
i++;//i需要后移
}else{
//如果是一个数,需要考虑一个多位数的问题
str = "";//先将str置成空串
while(i < s.length() && (c =s.charAt(i))>=48 && (c = s.charAt(i))<=57){
str +=c;
i++;
}
ls.add(str);
}
}while (i < s.length());
return ls;
}
//将逆波兰表达式依次将数据和运算符放入到arraylist中
public static List<String> getListString(String suffixExpression){
//将suffixExpression分割
String[] splits = suffixExpression.split(" ");
ArrayList<String> arrayList = new ArrayList<>();
for (String ele : splits){
arrayList.add(ele);
}
return arrayList;
}
//完成对逆波兰表达式的扫描,也就是遍历
public static int calculate(List<String> list){
//创建一个栈,只需要一个栈即可
Stack<String> stack = new Stack<>();
//遍历list
for (String items :list){
//使用正则表达式取出数
if (items.matches("\\d+")){
//匹配的是多位数
//入栈
stack.push(items);
}else{
//pop两个数,运算,再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res =0;
if (items.equals("+")){
res = num1+num2;
}else if (items.equals("-")){
res = num1-num2;
}else if (items.equals("*")){
res = num1*num2;
}else if (items.equals("/")){
res =num1/num2;
}else{
throw new RuntimeException("运算符有误!");
}
//把res入栈
stack.push(""+res);
}
}
//最后留在stack中的数据是运算结果
return Integer.parseInt(stack.pop());
}
}
//编写一个类Operation,可以返回一个运算符对应的优先级
class Operation{
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
//写一个方法,用来返回对应的优先级数字
public static int getValue(String operation){
int result =0;
switch (operation){
case "+":
result = ADD;
break;
case "-":
result = SUB;
break;
case "*":
result = MUL;
break;
case "/":
result = DIV;
break;
default:
System.out.println("不存在该运算符!");
break;
}
return result;
}
}
代码运行如图:
