毕业设计——第三章 开发方法及系统实现(5)
3.6.2两线交点
这里采用了数学里面的两直线的交点的算法。
(1) 问题描述:已知两直线上的两点Line1(pt10,pt11),Line2(pt20,pt21),求交点PtX;
(2) 算法描述:先根据直线上的两点,求出两直线方程,根据两直线方程求出其交点。
(3) 算法实现:设置两直线Line1(pt10,pt11),Line2(pt20,pt21);
(a) 初始时,先检查两直线的点是否为特殊点,比如:pt10.X与pt11.X的值是否相同,如果相同,则返回特殊值;
(b) 根据两直线方程,利用数学知识上的两直线交点的求解方式进行求解,求交点。
3.6.3高程求解
使用了数据里面的相似定律里面的知识来进行高程求解。
(1) 问题描述:在图上已知地形的高程点A、B、C,求图上任意一点的高程坐标E。
(2) 算法描述:先确定用户在图上点击坐标点E的二维坐标,即:(E.X,E.Y),根据该点找到离它最近点A,同时找出离它最近的A、B、C三个点,构成一个三角型(如果不能构成三角成,则作为特殊情况来处理),现求出BC边上的D点的高程坐标,再根据D点坐标,利用直线AD,求出点E过程。
|
|
图 3-1 高程求解
(3) 算法实现:
(a) 求出AE,AC,AB的距离,找出最小的线距AE;
(b) 连接AE,BC,构成两直线,并求出交点D;
(c) 根据如下公式来D点高程Z
d:
(d) 在直线AD,利用(3)里面的公式,计算E点高程。
3.6.4管段数据的存储
由于管段的数据是根据图上的标示来表示,同时必须记录图上的信息,由于本系统开发是基于GIS系统开发,同时结合给排水系统的特点,排水系统采用了树状结构表示,所以,记录管段数据时必须必须将树状的结构信息记录入数据。参考图论中的无环有相图来记录数据,举例如下:
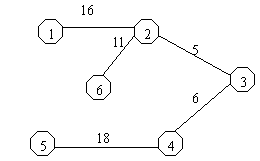
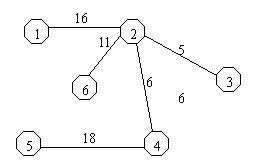
|
|